2019年湖北省鄂州市中考数学

2019年湖北省鄂州市中考数学

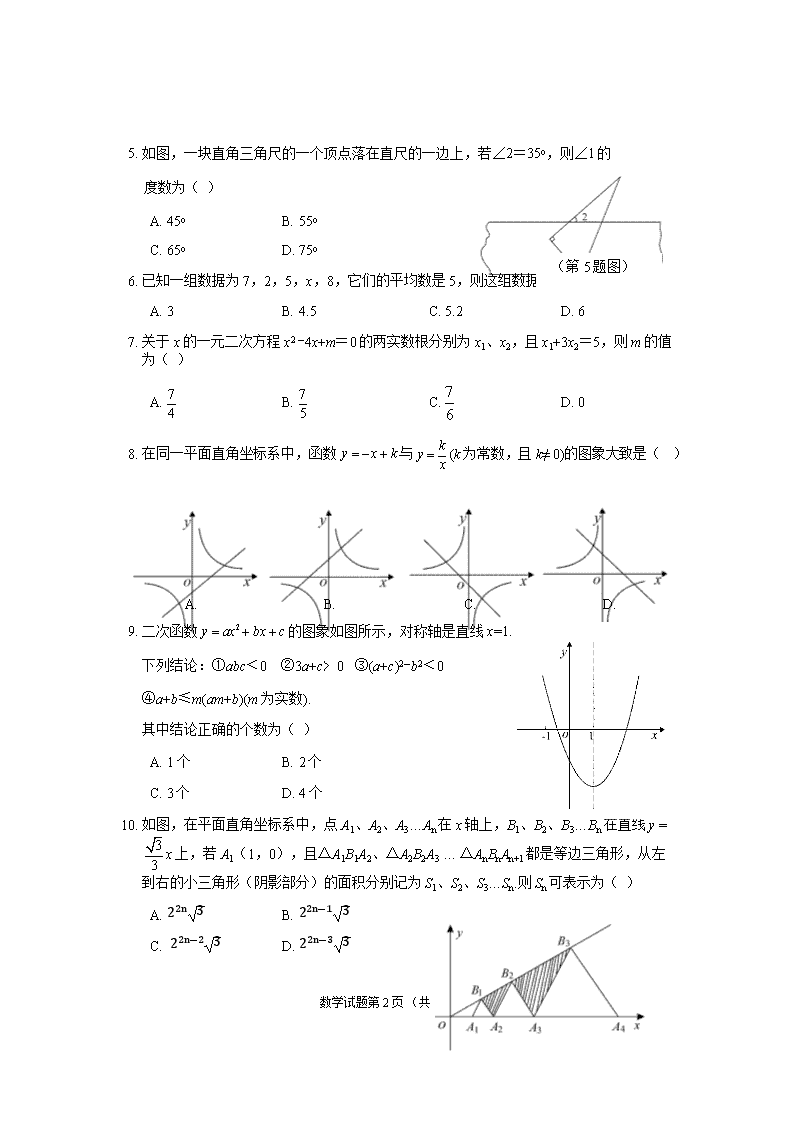
数学试题第 1 页 （共 13 页） 鄂州市 2019 年初中毕业生学业考试 数 学 试 题 学校：________考生姓名：________ 准考证号： 注意事项： 1．本试题卷共 6 页，满分 120 分，考试时间 120 分钟。 2．答题前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号 条形码粘贴在答题卡上的指定位置。 3．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改动， 用橡皮擦干净后，再选涂其他答案标号。答在试题卷上无效。 4．非选择题用 0.5 毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内。答在试题卷 上无效。 5．考生必须保持答题卡的整洁。考试结束后，请将本试题卷和答题卡一并上交。 6．考生不准使用计算器。 一、选择题（每小题 3 分，共 30 分） 1. -2019 的绝对值是（ ） A. 2019 B.-2019 C. D. 2. 下列运算正确的是（ ） A. a3·a2 = a6 B. a7÷a3 = a4 C. (-3a)2 = -6a2 D. (a -1)2= a2 -1 3. 据统计，2019 年全国高考人数再次突破千万，高达 1031 万人.数据 1031 万用科学计数 法可表示为（ ） A. 0.1031×106 B. 1.031×107 C. 1.031×108 D. 10.31×109 4. 如图是由 7 个小正方体组合成的几何体，则其左视图为（ ） A. B. C. D. 1 2019 1 2019 − (第 4 题图) 数学试题第 2 页 （共 13 页） (第 9 题图) 5. 如图，一块直角三角尺的一个顶点落在直尺的一边上，若∠2＝35o，则∠1 的 度数为（ ） A. 45o B. 55o C. 65o D. 75o 6. 已知一组数据为 7，2，5，x，8，它们的平均数是 5，则这组数据的方差为（ ） A. 3 B. 4.5 C. 5.2 D. 6 7. 关于 x 的一元二次方程 x2 -4x+m＝0 的两实数根分别为 x1、x2，且 x1+3x2＝5，则 m 的值 为（ ） A. B. C. D. 0 8. 在同一平面直角坐标系中，函数 与 (k 为常数，且 k≠ 0)的图象大致是（ ） A. B. C. D. 9. 二次函数 的图象如图所示，对称轴是直线 x=1. 下列结论：①abc﹤0 ②3a+c﹥0 ③(a+c)2-b2﹤0 ④a+b≤m(am+b)(m 为实数). 其中结论正确的个数为（ ） A. 1 个 B. 2 个 C. 3 个 D. 4 个 10. 如图，在平面直角坐标系中，点 A1、A2、A3…An 在 x 轴上，B1、B2、B3…Bn 在直线 y = 上，若 A1（1，0），且△A1B1A2、△A2B2A3 … △AnBnAn+1 都是等边三角形，从左 到右的小三角形（阴影部分）的面积分别记为 S1、S2、S3…Sn.则 Sn 可表示为（ ） A. 22n 3 B. 22n―1 3 C. 22n―2 3 D. 22n―3 3 7 4 7 5 7 6 y x k= − + ky x = 2y ax bx c= + + 3 3 x （第 5 题图） 数学试题第 3 页 （共 13 页） 二.填空题（每小题 3 分，共 18 分） 11. 因式分解：4ax2 -4ax+a＝_______. 12. 若关于 x、y 的二元一次方程组 的解满足 x+y≤0，则 m 的取值范 围是___________. 13. 一个圆锥的底面半径 r＝5，高 h＝10，则这个圆锥的侧面积是________. 14. 在平面直角坐标系中,点 P（x0，y0）到直线 Ax+By+C=0 的距离公式为: ,则点 P（3，-3）到直线 的距离为_____. 15. 如图，已知线段 AB＝4，O 是 AB 的中点，直线 l 经过点 O，∠1＝60°，P 点是直线 l 上 一点，当△APB 为直角三角形时，则 BP＝____________. 16. 如图，在平面直角坐标系中，已知 C（3，4），以点 C 为圆心的圆与 y 轴相切.点 A、B 在 x 轴上，且 OA＝OB.点 P 为⊙C 上的动点，∠APB＝90°,则 AB 长度的最大值为 _______. 3 4 3 5 5 x y m x y − = +  + = 0 0 2 2 Ax By Cd A B + += + 2 5 3 3y x= − + (第 10 题图) (第 15 题图) (第 16 题图) 题图图 数学试题第 4 页 （共 13 页） 三.解答题（17～21 题每题 8 分，22、23 题每题 10 分，24 题 12 分，共 72 分） 17. (本题满分 8 分)先化简，再从-1、2、3、4 中选一个合适的数作为 x 的值代入求值. 18. (本题满分 8 分)如图，矩形 ABCD 中，AB＝8，AD＝6，点 O 是对角线 BD 的中点，过 点 O 的直线分别交 AB、CD 边于点 E、F. （1）求证：四边形 DEBF 是平行四边形; （2）当 DE＝DF 时，求 EF 的长. 19. (本题满分 8 分)某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的 喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中选出一类最喜爱的电 视节目，以下是根据调查结果绘制的统计图表的一部分. 类别 A B C D E 类型 新闻 体育 动画 娱乐 戏曲 人数 11 20 40 m 4 请你根据以上信息，回答下列问题： （1）统计表中 m 的值为____，统计图中 n 的值为____，A 类对应扇形的圆心角为____ 度； （2）该校共有 1500 名学生，根据调查结果，估计该校最喜爱体育节目的学生人数； （3）样本数据中最喜爱戏曲节目的有 4 人，其中仅有 1 名男生. 从这 4 人中任选 2 名同 学去观赏戏曲表演，请用树状图或列表求所选 2 名同学中有男生的概率. 2 2 2 2 4 4( )4 4 2 4 x x x x x x x − −− ÷− + − − (第 18 题图) (第 19 题图) 数学试题第 5 页 （共 13 页） (第 22 题图) 20. (本题满分 8 分)已知关于 x 的方程 x2 -2x+2k -1=0 有实数根. （1）求 k 的取值范围； （2）设方程的两根分别是 x1、x2，且 ，试求 k 的值. 21. (本题满分 8 分)为积极参与鄂州市全国文明城市创建活动，我市某校在教学楼顶部新建 了一块大型宣传牌，如下图.小明同学为测量宣传牌的高度 AB，他站在距离教学楼底部 E 处 6 米远的地面 C 处，测得宣传牌的底部 B 的仰角为 60°，同时测得教学楼窗户 D 处 的仰角为 30°（A、B、D、E 在同一直线上）.然后,小明沿坡度 i=1:1.5 的斜坡从 C 走到 F 处，此时 DF 正好与地面 CE 平行. （1）求点 F 到直线 CE 的距离(结果保留根号); （2）若小明在 F 处又测得宣传牌顶部 A 的仰角为 45°,求宣传牌的高度 AB（结果精确到 0.1 米， 2 ≈1.41， 3 ≈1.73）. 22.(本题满分 10 分)如图，PA 是⊙O 的切线，切点为 A, AC 是⊙O 的直径，连接 OP 交⊙O 于 E.过 A 点作 AB⊥PO 于点 D，交⊙O 于 B，连接 BC，PB. （1）求证：PB 是⊙O 的切线； （2）求证：E 为△PAB 的内心； （3）若 cos∠PAB= , BC =1，求 PO 的长. 2 1 1 2 1 2 x x x xx x + = ⋅ 10 10 （第 21 题图） 数学试题第 6 页 （共 13 页） 23. (本题满分 10 分)“互联网+”时代，网上购物备受消费者青睐. 某网店专售一款休闲裤， 其成本为每条 40 元，当售价为每条 80 元时，每月可销售 100 条.为了吸引更多顾客， 该网店采取降价措施. 据市场调查反映：销售单价每降 1 元，则每月可多销售 5 条. 设每 条裤子的售价为 x 元（x 为正整数），每月的销售量为 y 条. （1）直接写出 y 与 x 的函数关系式； （2）设该网店每月获得的利润为 w 元，当销售单价降低多少元时，每月获得的利润最 大，最大利润是多少？ （3）该网店店主热心公益事业，决定每月从利润中捐出 200 元资助贫困学生. 为了保证 捐款后每月利润不低于 4220 元，且让消费者得到最大的实惠，该如何确定休闲裤 的销售单价？ 24. （本题满分 12 分）如图，已知抛物线 y=-x2+bx+c 与 x 轴交于 A、B 两点，AB＝4，交 y 轴于点 C，对称轴是直线 x=1. （1）求抛物线的解析式及点 C 的坐标； （2）连接 BC，E 是线段 OC 上一点，E 关于直线 x=1 的对称点 F 正好落在 BC 上，求 点 F 的坐标； （3）动点 M 从点 O 出发，以每秒 2 个单位长度的速度向点 B 运动，过 M 作 x 轴的垂 线交抛物线于点 N，交线段 BC 于点 Q.设运动时间为 t(t>0)秒. ①若△AOC 与△BMN 相似，请直接写出 t 的值； ②△BOQ 能否为等腰三角形？若能，求出 t 的值；若不能，请说明理由. （第 24 题图） (第 24 题备用图 1） （第 24 题备用图 2） 数学试题第 7 页 （共 13 页） 鄂州市 2019 年初中毕业生学业考试 数学试题参考答案及评分标准 一、选择题（每小题 3 分，共 30 分） 1～5 A B B A B 6～10 C A C C D 二、填空题（每小题 3 分，共 18 分） 11. a(2x-1)2. 12. m≤-2. 13. 25 5π. 14. 8 13 13 15. 2 或 2 3或 2 7(说明：3 解中每对一个得 1 分，若有错误答案得 0 分) 16. 16 三、解答题 17.（8 分）解：原式＝x+2 ………… 4′ ∵ x-2≠0，x-4≠0 ∴ x≠2 且 x≠4 ………… 7′ ∴当 x=-1 时，原式＝－1+2＝1 ………… 8′ ① （或当 x=3 时，原式＝3+2＝5 ………… 8′）② 注：①或②任做对一个都可以 18. （1）证明：∵ 四边形 ABCD 是矩形 ∴ AB∥CD ∴ ∠DFO＝∠BEO， 又因为∠DOF＝∠BOE，OD＝OB ∴△DOF ≌ △BOE ∴DF＝BE 又因为 DF∥BE， ∴四边形 BEDF 是平行四边形. ………… 4′ （2）解：∵DE=DF，四边形 BEDF 是平行四边形 ∴ BEDF 是菱形 ∴ DE＝BE，EF⊥BD，OE＝OF 设 AE=x，则 DE＝BE=8-x 在 Rt△ADE 中，根据勾股定理，有 AE2+AD2＝DE2 ∴ x2+62= (8-x)2 解之得：x = 7 4 ∴ DE=8 - 7 4 = 25 4 ………… 6′ 在 Rt△ABD 中，根据勾股定理，有 AB2+AD2＝BD2 EA B CD F 第 18 题图 O 数学试题第 8 页 （共 13 页） ∴BD= 62 + 82 = 10 ∴ OD = 1 2 BD = 5, 在 Rt△DOE 中，根据勾股定理，有 DE2 - OD2＝OE2， ∴ OE = (25 4 ) 2 - 52 = 15 4 ∴ EF = 2OE= 15 2 ………… 8′ （此题有多种解法，方法正确即可分） 19. （1）25 25 39.6 ………… 3′ （2）1500× 20 100 = 300（人） 答：该校最喜爱体育节目的人数约有 300 人. ………… 5′ （3）P＝ 1 2 （说明：直接写出答案的只给 1 分， 画树状图或列表的按步骤给分） ………… 8′ 20. （1）解：∵原方程有实数根， ∴b2-4ac≥0 ∴(-2)2-4(2k-1) ≥0 ∴k≤1 ………… 3′ （2）∵x1,x2 是方程的两根，根据一元二次方程根与系数的关系，得： x1 + x2 ＝ 2，x1 ·x2 ＝2k-1 又∵ ∴x21 + x22 x1· x2 = x1· x2 ∴(x1 + x2)2-2x1 x2 = (x1 ·x2)2 ………… 5′ ∴ 22-2(2k-1)= (2k-1)2 解之，得： k1＝ 5 2 , k2 = ― 5 2 . 经检验，都符合原分式方程的根 ………… 6 ∵ k≤1 ………… 7′ ∴k = ― 5 2 . ………… 8′ 数学试题第 9 页 （共 13 页） 21.解：（1）过点 F 作 FG⊥EC 于 G， 依题意知 FG∥DE，DF∥GE，∠FGE＝90o ∴四边形 DEFG 是矩形 ∴FG＝DE 在 Rt△CDE 中， DE＝CE·tan∠DCE = 6×tan30 o =2 3 （米） ∴点 F 到地面的距离为 2 3 米. …………3′ (2) ∵斜坡 CF i＝1：1.5 ∴Rt△CFG 中，CG＝1.5FG＝2 3 ×1.5＝3 3 ∴FD＝EG＝3 3 +6 ………… 5′ 在 Rt△BCE 中， BE＝CE·tan∠BCE = 6×tan60 o ＝6 3 ………… 6′ ∴AB=AD+DE-BE =3 3+6+2 3-6 3=6- 3≈4.3 (米) 答：宣传牌的高度约为 4.3 米. ………… 8′ 22.（1）证明：连结 OB ∵AC 为⊙O 的直径 ∴∠ABC＝90o 又∵AB⊥PO ∴PO∥BC ∴∠AOP＝∠C，∠POB＝∠OBC (第 22 题图) A P B O C D E F C E A B D 第 21 题图 G 数学试题第 10 页 （共 13 页） 而 OB＝OC ∴∠OBC＝∠C ∴∠AOP＝∠POB 在△AOP 和△BOP 中 { OA＝OB ∠ AOP＝∠ POB PO＝PO ∴△AOP≌△BOP ∴∠OBP＝∠OAP ∵PA 为⊙O 的切线 ∴∠OAP＝90o ∴∠OBP＝90o ∴PB 是⊙O 的切线 …………3′ （2）证明：连结 AE ∵PA 为⊙O 的切线 ∴∠PAE+∠OAE＝90o ∵AD⊥ED ∴∠EAD+∠AED＝90o ∵OE＝OA ∴∠OAE＝∠AED ∴∠PAE＝∠DAE 即 EA 平分∠PAD ∵PA、PD 为⊙O 的切线 ∴PD 平分∠APB ∴E 为△PAB 的内心 …………6′ （3）∵∠PAB+∠BAC=90o ∠C+∠BAC=90o ∴∠PAB=∠C ∴cos∠C = cos∠PAB= 10 10 在 Rt△ABC 中，cos∠C＝ BC AC ＝ 1 AC = 10 10 ∴AC＝ 10，AO＝ 10 2 …………8′ 由△PAO∽△ABC ∴ PO AC ＝ AO BC ∴PO＝ AO BC ·AC ＝ 10 2 1 · 10＝5 …………10′ （此题有多种解法，解法正确即可） 23.解：（1）y＝100+5（80－x）或 y＝－5x+500 …………2′ 数学试题第 11 页 （共 13 页） （2）由题意，得： W=(x-40)( －5x+500) =-5x2+700x-20000 =-5(x-70)2+4500 …………4′ ∵a=-5<0 ∴w 有最大值 即当 x=70 时，w 最大值＝4500 ∴应降价 80－70＝10（元） 答：当降价 10 元时，每月获得最大利润为 4500 元 …………6′ （3）由题意，得： -5(x-70)2+4500＝4220+200 解之，得： x1＝66 x2 ＝74 …………8′ ∵抛物线开口向下，对称轴为直线 x=70， ∴当 66≤x≤74 时 ，符合该网店要求 而为了让顾客得到最大实惠 ， 故 x＝66 ∴当销售单价定为 66 元时，即符合网店要求，又能让顾客得到最大 实惠. …………10′ 24.解：（1））∵点 A、B 关于直线 x=1 对称，AB＝4 ∴A（－1，0），B（3，0） …………1′ 代入 y=-x2+bx+c 中，得： { -9 + 3b + c = 0 -1 ― b + c = 0 解得 {b = 2 c = 3 ∴抛物线的解析式为 y=-x2+2x+3 …………2′ ∴C 点坐标为（0，3） …………3′ 数学试题第 12 页 （共 13 页） （2）设直线 BC 的解析式为 y=mx+n，则有： { n = 3 3m + n = 0 解得 {m = -1 n = 3 ∴直线 BC 的解析式为 y=-x+3 …………4′ ∵点 E、F 关于直线 x=1 对称 ， 又 E 到对称轴的距离为 1， ∴ EF=2 ∴F 点的横坐标为 2，将 x=2 代入 y=-x+3 中， 得：y=-2+3=1 ∴F（2，1） …………6′ （3）○1t=1 (若有 t = 3 2 ,则扣 1 分) …………9′ ○2∵M（2t,0）,MN⊥x 轴 ∴Q（2t,3-2t） ∵△BOQ 为等腰三角形, ∴分三种情况讨论 第一种，当 OQ＝BQ 时， ∵QM⊥OB ∴OM＝MB ∴2t=3-2t ∴t= 3 4 …………10′ 第二种，当 BO＝BQ 时，在 Rt△BMQ 中 ∵∠OBQ ＝45O ∴ BQ＝ 2BM x y O A B C (第 24 题) 图 N Q M x y O A B C 第 24 题备用图 图)1 数学试题第 13 页 （共 13 页） ∴BO＝ 2BM 即 3＝ 2(3 ― 2t) ∴t＝ 6 - 3 2 4 …………11′ 第三种，当 OQ＝OB 时，则点 Q、C 重合，此时 t=0 而 t>0，故不符合题意 综上述，当 t= 3 4秒或6 - 3 2 4 秒时，△BOQ 为等腰三角 形. …………12′（解法正确即可）