中考数学二模试题及答案

中考数学二模试题及答案

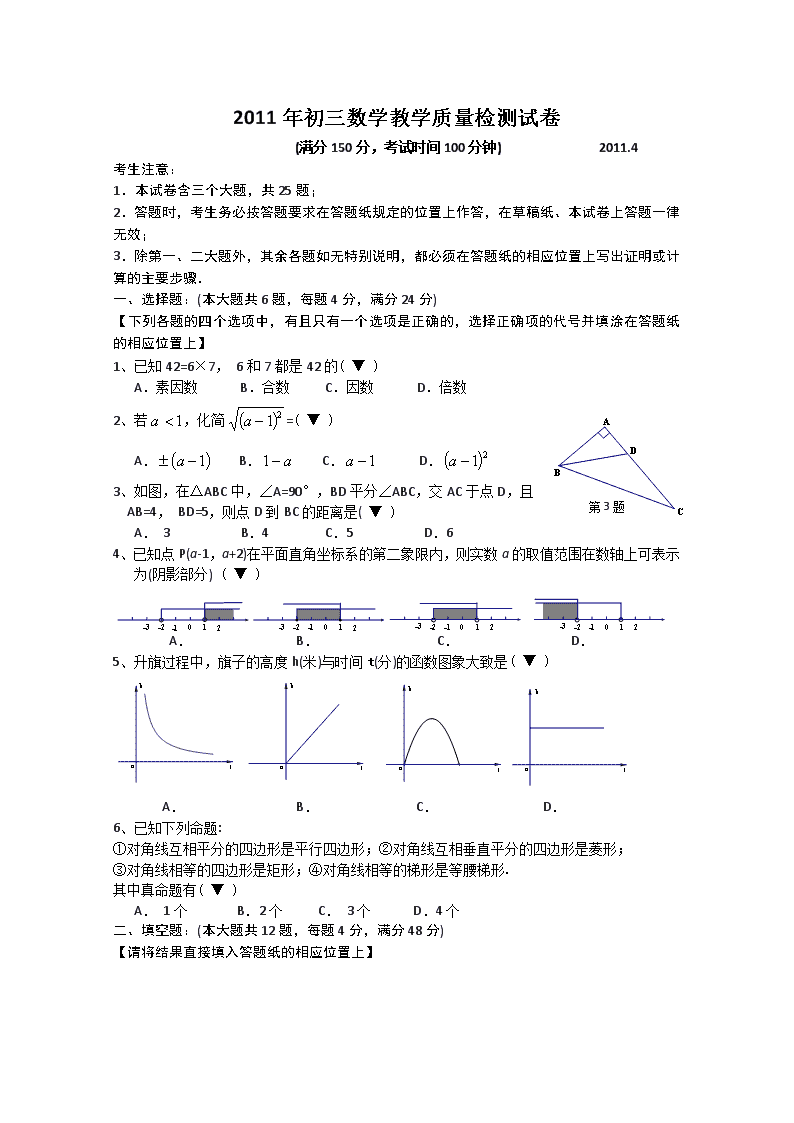
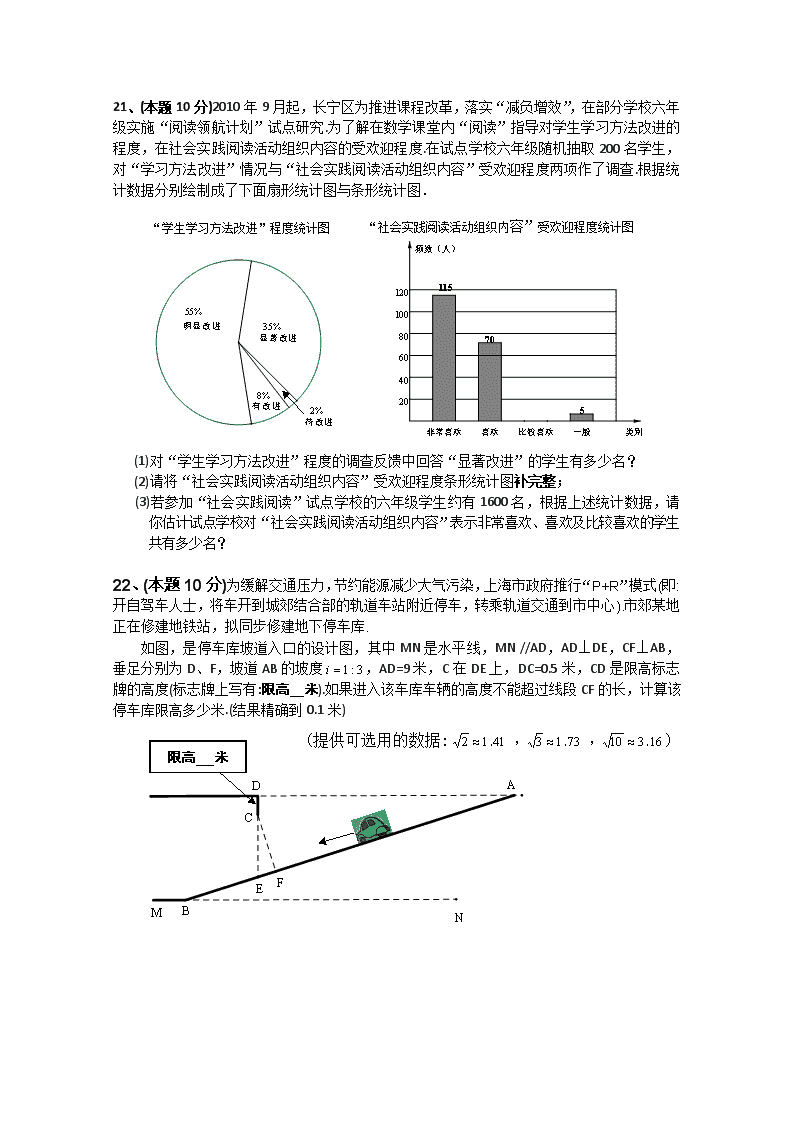
‎2011年初三数学教学质量检测试卷 ‎ (满分150分，考试时间100分钟) 2011.4‎ 考生注意：‎ ‎1．本试卷含三个大题，共25题；‎ ‎2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；‎ ‎3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：(本大题共6题，每题4分，满分24分)‎ ‎【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】‎ ‎1、已知42=6×7， 6和7都是42的( ▼ )‎ A．素因数 B．合数 C．因数 D．倍数 第3题 ‎2、若，化简=( ▼ )‎ A． B． C． D．‎ ‎3、如图，在△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且 ‎ AB=4， BD=5，则点D到BC的距离是( ▼ )‎ A． 3 B．‎4 C．5 D．6‎ ‎4、已知点P(a-1，a+2)在平面直角坐标系的第二象限内，则实数a的取值范围在数轴上可表示为(阴影部分) ( ▼ )‎ A． B． C． D．‎ ‎5、升旗过程中，旗子的高度h(米)与时间t(分)的函数图象大致是( ▼ )‎ A． B． C． D．‎ ‎6、已知下列命题:‎ ‎①对角线互相平分的四边形是平行四边形；②对角线互相垂直平分的四边形是菱形；‎ ‎③对角线相等的四边形是矩形；④对角线相等的梯形是等腰梯形.‎ 其中真命题有( ▼ )‎ A． 1个 B．2个 C． 3个 D．4个 二、填空题：(本大题共12题，每题4分，满分48分)‎ ‎【请将结果直接填入答题纸的相应位置上】‎ ‎7、因式分解:= ▼ . ‎ ‎8、计算: = ▼ .‎ ‎9、已知点A( -3,2)与点B关于y轴对称，若反比例函数的图像经过点B，则的图像在x < 0时y随x的增大而 ▼ . (填“增大”或“减小”)‎ ‎10、2010年以“城市让生活更美好”为主题的上海世博会成功举办.在‎2010年10月16日上海世博会单日入园人数1032700人，刷新世博会单日入园人数的历史记录.将1032700用科学记数法表示为▼ .‎ ‎11、已知Rt△ABC中，在斜边BC上取一点D，使得BD=CD，则BC:AD的比值为 ▼ . .‎ 第13题 ‎12、已知函数，当x = ▼ 时.‎ ‎13、如图所示，一块正八边形的游戏板，用纸板沿着正八边形的边做一围栏，随意投掷一个骰子.规定:如果骰子落在分界线上，则算落在其逆时针方向的区域.骰子落在黑色区域的概率是 ▼ .‎ ‎14、已知平行四边形ABCD(AB>BC)，分别以点A、B、C、D为起点 第16题 或终点的向量中，与向量的模相等的向量是 ▼ .‎ ‎15、已知△ABC中，D是BC边上的点，AD恰是BC边上的垂直 平分线，如果，则= ▼ .‎ ‎16、如图，在直角坐标系中，以点P为圆心的圆弧与x轴交于A、B 第18题 两点，已知P(4，2)和A(2，0)，则点B的坐标是 ▼ .‎ ‎17、长度为2的线段AB被点P分成AP和BP两段，已知较长的线段 BP是AB与AP的比例中项，则较短的一条线段AP的长为 ▼ .‎ ‎18、 如图，将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折 叠， 使点A与BC边上的点E重合，折痕交AB于点F.若BE:EC=m:n，‎ 则AF:FB= ▼ .‎ 三、解答题：(本大题共7题，满分78分)‎ ‎19、(本题10分)计算:‎ ‎20、(本题10分)解方程: ‎ ‎21、(本题10分)2010年9月起，长宁区为推进课程改革，落实“减负增效”，在部分学校六年级实施“阅读领航计划”试点研究.为了解在数学课堂内“阅读”指导对学生学习方法改进的程度，在社会实践阅读活动组织内容的受欢迎程度.在试点学校六年级随机抽取200名学生，对“学习方法改进”情况与“社会实践阅读活动组织内容”受欢迎程度两项作了调查.根据统计数据分别绘制成了下面扇形统计图与条形统计图．‎ ‎“学生学习方法改进”程度统计图 ‎“社会实践阅读活动组织内容”受欢迎程度统计图 ‎(1)对“学生学习方法改进”程度的调查反馈中回答“显著改进”的学生有多少名？ ‎ ‎(2)请将“社会实践阅读活动组织内容”受欢迎程度条形统计图补完整；‎ ‎(3)若参加“社会实践阅读”试点学校的六年级学生约有1600名，根据上述统计数据，请你估计试点学校对“社会实践阅读活动组织内容”表示非常喜欢、喜欢及比较喜欢的学生共有多少名？‎ ‎22、(本题10分)为缓解交通压力，节约能源减少大气污染，上海市政府推行“P+R”模式(即:开自驾车人士，将车开到城郊结合部的轨道车站附近停车，转乘轨道交通到市中心).市郊某地正在修建地铁站，拟同步修建地下停车库.‎ 如图，是停车库坡道入口的设计图，其中MN是水平线，MN //AD，AD⊥DE，CF⊥AB，垂足分别为D、F，坡道AB的坡度，AD=‎9米，C在DE上，DC=‎0.5米，CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长，计算该停车库限高多少米.(结果精确到‎0‎‎.1米)‎ 限高 米 ‎(提供可选用的数据:)‎ ‎23、(本题12分)如图，在平面直角坐标系中，等腰梯形OABC，CB//OA，且点A在x轴正半轴上.已知C(2，4)，BC= 4.‎ ‎(1)求过O、C、B三点的抛物线解析式，并写出顶点坐标和对称轴；‎ ‎(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合)，使得P点到两坐标轴的距离相等.如果存在，求出P点坐标；如果不存在，请说明理由.‎ ‎24、 (本题12分)如图，AD//BC，点E、F在BC上，∠1=∠2，AF⊥DE，垂足为点O.‎ ‎(1)求证:四边形AEFD是菱形；‎ ‎(2)若BE=EF=FC，求∠BAD+∠ADC的度数；‎ ‎(3)若BE=EF=FC，设AB = m，CD = n，求四边形ABCD的面积.‎ ‎25、 (本题14分)如图，在平面直角坐标系中，抛物线与 x轴交于A、B两点(A点在B点左侧)，与y轴交于C点，顶点为D.过点 C、D的直线与x轴交于E点，以OE为直径画⊙O1，交直线CD于P、E 两点.‎ ‎(1)求E点的坐标；‎ ‎(2)联结PO1、PA.求证:～；‎ ‎(3) ①以点O2 (0，m)为圆心画⊙O2，使得⊙O2与⊙O1相切，‎ 当⊙O2经过点C时，求实数m的值；‎ ‎②在①的情形下，试在坐标轴上找一点O3，以O3为圆心画 ‎⊙O3，使得⊙O3与⊙O1、⊙O2同时相切.直接写出满足条件的点O3的坐标(不需写出计算过程).‎ ‎2011年初三数学教学质量检测试卷参考答案 一、 选择题 ‎ ‎1C‎ 2B ‎3A ‎4C 5B ‎‎6C 二、 填空题 ‎7、 8、 9、减小 10、 11、2 ‎ ‎12、2 13、(或0.375) 14、 15、 16、（6,0）‎ ‎17、 18、‎ 三、解答题 ‎19（10分）解：原式= 6分 ‎ = 2分 ‎ = 1 2分 ‎20（10分）解：令 1分 解：原方程化为： 2分 原方程化为 当时， ‎ 整理得 2分 整理得： 3分 解得 2分 解得：、 2分 当时 解得 （若前面无“当时”在此应当检验） 2分 当时 解得 2分 ∴原方程的解是、 1分 经检验:,是原方程的解 2分 ‎ ‎∴原方程的解是、 1分 ‎21（10分）(1)70 3分 ‎ (2)10 4分 ‎ (3)1560 3分 ‎ ‎22（10分）解：据题意得 ‎ ‎ ∵MN//AD ∴∠A=∠B ∴ ‎ ‎∵DE⊥AD ∴在Rt△ADE中 ∵AD=9 ∴DE=3 2分 又∵DC=0.5 ∴CE=2.5 ‎ ‎∵CF⊥AB ∴∠1+∠2=90°‎ ‎∵DE⊥AD ∴∠A+∠2=90° ‎ ‎∴∠A =∠1 ∴ 2分 在Rt△CEF中 ‎ 设EF=x CF=3x（x>0） CE=2.5 ‎ 代入得 ‎ 解得 （如果前面没有 “设”,则此处应“，舍负”）3分 ‎∴CF=3x= 2分 ‎∴该停车库限高‎2.3米. 1分 ‎23（12分）解：(1) ( 6分）∵C(2,4), BC=4 且 BC//OA ∴ B(6,4) 1分 设抛物线为 ‎ 将O(0,0),C(2,4),B(6,4)代入得 解得 3分 ‎∴ 1分 ‎∴顶点 对称轴：直线 2分 ‎(2) (6分)据题意，设或 1分 将代入抛物线得 解得(舍) 2分 将代入抛物线得 解得(舍) 2分 ‎∴符合条件的点和 1分 ‎24（12分）（1）( 4分）证明:（方法一）∵AF⊥DE ‎ ‎∴∠1+∠3=90° 即：∠3=90°-∠1‎ ‎ ∴∠2+∠4=90° 即：∠4=90°-∠2‎ ‎ 又∵∠1=∠2 ∴∠3=∠4 ∴AE = EF ‎ ‎∵AD//BC ∴∠2=∠5 ‎ ‎∵∠1=∠2 ∴∠1=∠5‎ ‎∴AE = AD ∴EF = AD 2分 ‎∵AD//EF ‎ ‎∴四边形AEFD是平行四边形 1分 又∵AE = AD ‎ ‎∴四边形AEFD是菱形 1分 ‎（方法二）∵AD//BC ∴∠2=∠5‎ ‎ ∵∠1=∠2 ∴∠1=∠5‎ ‎∵AF⊥DE ∴∠AOE=∠AOD=90°‎ 在△AEO和△ADO中 ∴△AEO△ADO ∴EO=OD ‎6‎ 在△AEO和△FEO中 ∴△AEO△FEO ∴AO=FO 2分 ‎∴AF与ED互相平分 1分 ‎∴四边形AEFD是平行四边形 又∵AF⊥DE ‎∴四边形AEFD是菱形 1分 ‎(2)( 5分）∵菱形AEFD ∴AD=EF ‎ ‎∵BE=EF ∴AD=BE 又∵AD//BC ∴四边形ABED是平行四边形 1分 ‎∴AB//DE ∴∠BAF=∠EOF 同理可知 四边形AFCD是平行四边形 ‎∴AF//DC ∴∠EDC=∠EOF 又∵AF⊥ED ∴∠EOF=∠AOD=90°‎ ‎∴∠BAF=∠EDC=∠EOF=90° 2分 ‎∴∠5 +∠6=90° 1分 ‎∴∠BAD+∠ADC=∠BAF+∠6 +∠5+∠EDC =270° 1分 ‎（3）( 3分）由（2）知∠BAF =90°平行四边形AFCD ∴AF=CD=n ‎ 又∵AB=m 1分 由（2）知 平行四边形ABED ∴DE=AB=m 由（1）知OD= 1分 ‎ 1分 ‎25（14分）解:(1) ( 3分) ∴ 1分 ‎ 设直线CD: 将C、D代入得 解得 ‎ ‎ ∴CD直线解析式: 1分 1分 ‎(2) ( 4分)令y=0 得 解得 ‎∴ 1分 又∵、 ∴以OE为直径的圆心、半径.‎ 设 ‎ 由 得 解得（舍）‎ ‎∴ 2分 ‎∴ ‎ 又 ‎ ‎∴ 1分 ∴～ ‎ ‎(3) ( 7分）① ‎ 据题意，显然点在点C下方 ‎ ‎ 当⊙O2与⊙O1外切时 ‎ 代入得 解得 （舍）2分 当⊙O2与⊙O1内切时 ‎ 代入得 解得 （舍） 2分 ‎∴ ‎ ‎② 3分 ‎ ‎