南京市2013年中考数学卷

南京市2013年中考数学卷

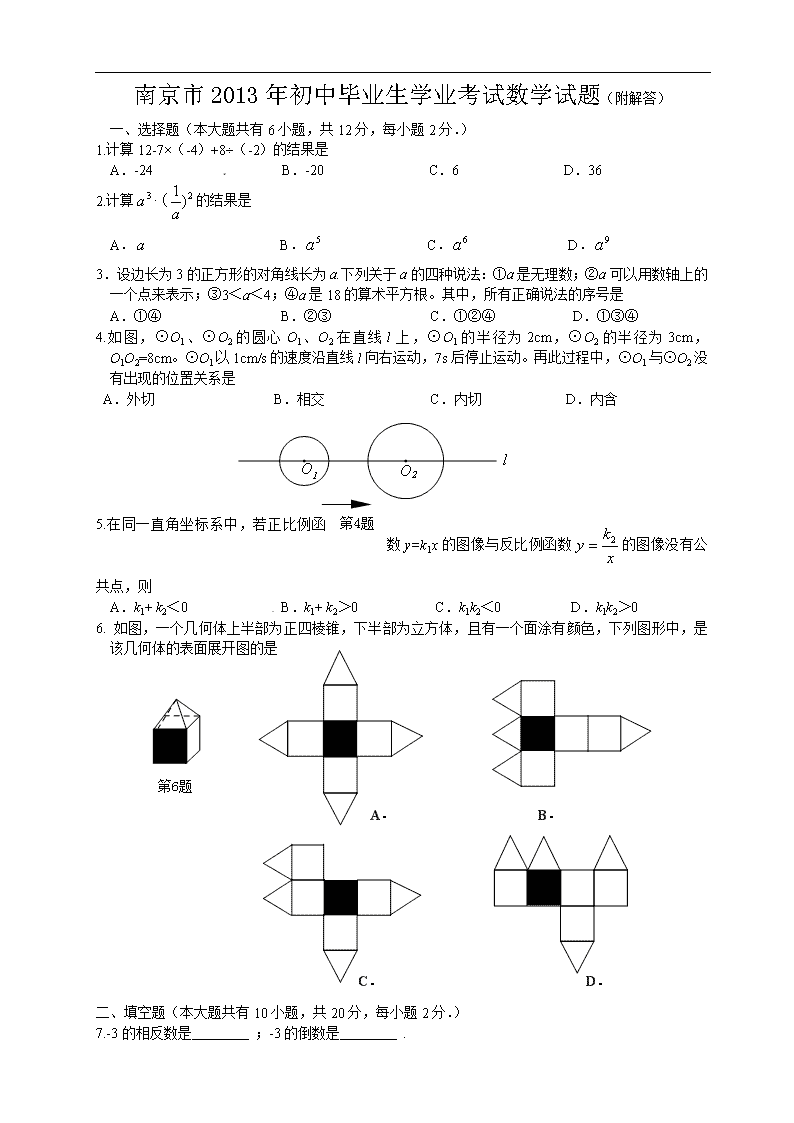
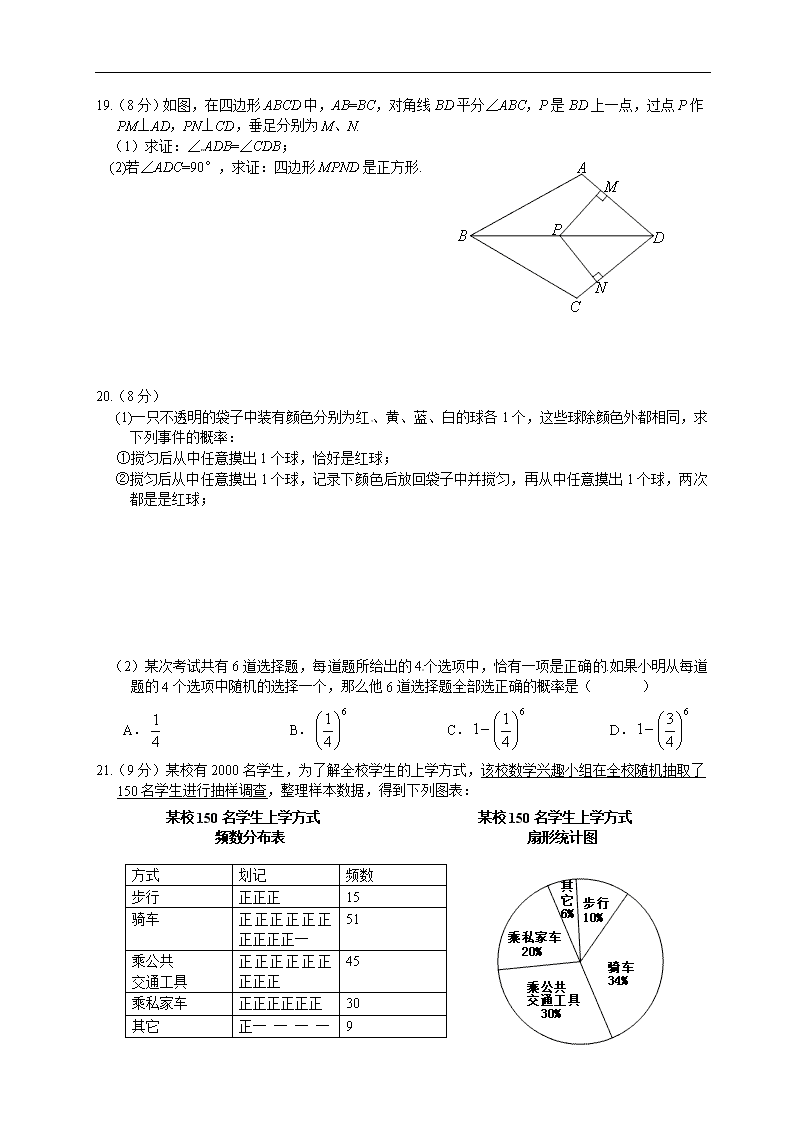
南京市2013年初中毕业生学业考试数学试题（附解答）‎ 一、选择题（本大题共有6小题，共12分，每小题2分．）‎ ‎1.计算12-7×（-4）+8÷（-2）的结果是 A．-24 B．-20 C．6 D．36‎ ‎2.计算的结果是 A． B． C． D．‎ ‎3．设边长为3的正方形的对角线长为a.下列关于a的四种说法：①a是无理数；②a可以用数轴上的一个点来表示；③3＜a＜4；④a是18的算术平方根。其中，所有正确说法的序号是 A．①④ B．②③ C．①②④ D．①③④‎ ‎4.如图，⊙O1、⊙O2的圆心O1、O2在直线l上，⊙O1的半径为2cm，⊙O2的半径为3cm，O1O2=8cm。⊙O1以1cm/s的速度沿直线l向右运动，7s后停止运动。再此过程中，⊙O1与⊙O2没有出现的位置关系是 A．外切 B．相交 C．内切 D．内含 ‎5.在同一直角坐标系中，若正比例函数y=k1x的图像与反比例函数的图像没有公共点，则 A．k1+ k2＜0 B．k1+ k2＞0 C．k1k2＜0 D．k1k2＞0‎ A．‎ B．‎ C．‎ D．‎ ‎6. 如图，一个几何体上半部为正四棱锥，下半部为立方体，且有一个面涂有颜色，下列图形中，是该几何体的表面展开图的是 二、填空题（本大题共有10小题，共20分，每小题2分．）‎ ‎7.-3的相反数是 ；-3的倒数是 .‎ ‎8.计算的结果是 .‎ ‎9.使式子有意义的x的取值范围是 .‎ ‎10.第二节亚洲青年运动会将于‎2013年8月16日至24日在南京举办，在此期间约有13000名青少年志愿者提供服务，将13000用科学计数法表示为 .‎ ‎11.如图将矩形ABCD绕点A顺时针旋转到AB’C’D’的位置，旋转角α（0°＜α＜90°）.若 ‎∠1=110°，则∠α= °.‎ ‎12. 如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF.若菱形ABCD的边长为2cm，∠A=120°，则EF= cm .‎ ‎13.△OAB是以正多边形相邻的两个顶点A、B与它的中心O为顶点的三角形，若△OAB的一个内角为70°，则该正多边形的边数为 .‎ ‎14. 已知如图所示的图形的面积为24，根据图中的条件，可列出方程 .‎ ‎15. 如图，在梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点P，已知A（2,3），B(1,1),‎ x x+1‎ ‎1+x x A D B C P y x O D(4,3),则点P的坐标为（ ， ）. ‎ ‎16.计算的结果是 .‎ 三、解答题（本大题共有11小题，共88分．）‎ ‎17.（6分）化简. 18.（6分）解方程 ‎19.（8分）如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M、N.‎ ‎（1）求证：∠ADB=∠CDB；‎ ‎(2)若∠ADC=90°，求证：四边形MPND是正方形. ‎ ‎20.（8分）‎ ‎(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个，这些球除颜色外都相同，求下列事件的概率：‎ ‎①搅匀后从中任意摸出1个球，恰好是红球；‎ ‎②搅匀后从中任意摸出1个球，记录下颜色后放回袋子中并搅匀，再从中任意摸出1个球，两次都是是红球；‎ ‎（2）某次考试共有6道选择题，每道题所给出的4个选项中，恰有一项是正确的.如果小明从每道题的4个选项中随机的选择一个，那么他6道选择题全部选正确的概率是（ ）‎ A． B． C． D．‎ ‎21.（9分）某校有2000名学生，为了解全校学生的上学方式，该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查，整理样本数据，得到下列图表：‎ 某校150名学生上学方式 ‎ 扇形统计图 某校150名学生上学方式 ‎ 频数分布表 方式 划记 频数 步行 正正正 ‎15‎ 骑车 正正正正正正正正正正一 ‎51‎ 乘公共 交通工具 正正正正正正正正正 ‎45‎ 乘私家车 正正正正正正 ‎30‎ 其它 正一 一 一 一 ‎9‎ 合计 ‎150‎ ‎（1）理解画线语句的含义，回答问题：如果150名学生全部在同一个年级抽取，这样的抽样是否合理？请说明理由；‎ ‎（2）根据抽样调查的结果，将估计出的全校2000名学生上学方式的情况绘制成条形统计图：‎ 某校2000名学生上学方式条形统计图 步行 骑车 乘公共 乘私 其它 上学方式 ‎ 交通工具 家车 ‎700‎ ‎600‎ ‎500‎ ‎400‎ ‎300‎ ‎200‎ ‎100‎ ‎0‎ 人数 ‎（3）该校数学兴趣小组结合调查获取的信息，向学校提出了一些建议，如：骑车上学的学生数约占全校的34%，建议学生合理安排自行车停车场地，请你结合上述统计的全过程，再提出一条合理化建议： .‎ A O B H α ‎①‎ O A B H β ‎②‎ ‎22.（8分）已知不等臂跷跷板AB长4m，如图①，当AB的一端A碰到地面时，AB与地面的夹角为α；如图②，当AB的另一端B碰到地面时，AB与地面的夹角为β.求跷跷板AB的支撑点O到地面的高度OH.（用含α、β的式子表示）‎ ‎23.（8分）某商场促销方案规定：商场内所有商品按标价的80%出售，同时，当顾客在商场内消费满一定金额后，按下表获得相应返回金额.‎ 消费金额（元）‎ ‎300~400‎ ‎400~500‎ ‎500~600‎ ‎600~700‎ ‎700~900‎ ‎···‎ 返还金额（元）‎ ‎30‎ ‎60‎ ‎100‎ ‎130‎ ‎150‎ ‎···‎ 注：300~400表示消费金额大于300元且小于或等于400元，其他类同.‎ 根据上述促销方案，顾客在该商场购物可以获得双重优惠，例如，若购买标价为400元的商品，则消费金额为320元，获得的优惠额为400×(1-80%)+30=110（元）‎ ‎（1）购买一件标价为1000元的商品，顾客获得的优惠额是多少？‎ ‎（2）如果顾客购买标价不超过800元的商品，要使获得的优惠额不少于226元，那么该商品的标价至少为多少元？‎ ‎24.（8分）小丽驾车从甲地到乙地，设她出发第xmin时的速度为ykm/h，图中折线表示她在整个驾车过程中第y与 x 之间的函数关系.‎ ‎（1）小丽驾车的最高速度是 km/h;‎ ‎(2)当20≤x≤30时，求y与 x 之间的函数关系式，并求出小丽出发第22min时的速度；‎ ‎（3）如果汽车每行驶100km耗油10L，那么小丽驾车从甲地到乙地共耗油多少升？‎ ‎10 20 30 40 50 x(min)‎ ‎72‎ ‎48‎ ‎24‎ O y (km/h)‎ A B C D E F G 方法指导 如果物体的运动速度随着时间均匀增加（或减少），那么其在某个时间段内的平均速度为该时间段开始时刻的速度与结束时刻的速度的平均数。例如，由图像可知，第5min到第10min汽车的速度随着时间均匀增加，因此汽车在该时间段内的平均速度为=36（km/h）。该时间段行驶的路程为=3（km）‎ ‎25.（8分）如图，AD是⊙O的切线，切点为A，AB是⊙O的弦，过点B作BC∥AD，交⊙O于点C，连接AC，过点C作CD∥AB，交AD于点D，连接AO并延长交BC于点M，交过点C的直线于点P，且∠BCP=∠ACD .‎ ‎（1）判断直线PC与⊙O的位置关系，并说明理由；‎ ‎（2）若AB=9，BC=6，求PC 的长. ‎ ‎26.（9分）已知二次函数（a、m为常数，且a≠0）.‎ ‎（1）求证：不论a与m为何值，该函数的图象与x轴总有两个公共点；‎ ‎（2）设该函数的图象的顶点为C，与x轴交于A，B两点，与y轴交于点D.‎ ‎①当△ABC的面积等于1时，求a的值；‎ ‎②当△ABC的面积与△ABD的面积相等时，求m的值.‎ ‎27.（10分）对于两个相似三角形，如果沿周界按对应点顺序环绕方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似。‎ 例如，‎ 如图①，△ABC∽△A‘B‘C‘，且沿周界ABCA与A‘B‘C‘A‘环绕的方向相同，因此△ABC与△A‘B‘C‘互为顺相似；‎ 如图②△ABC∽△A‘B‘C‘，且沿周界ABCA与A‘B‘C‘A‘环绕的方向相反，因此△ABC与△A‘B‘C‘互为逆相似；‎ A B C A B C A‘‎ B‘‎ C‘‎ A‘‎ C‘‎ B‘‎ ‎①‎ ‎②‎ ‎（1）根据图Ⅰ、图Ⅱ和图Ⅲ满足的条件，可得下列三对相似三角形：①△ADE与△ABC;②△GHO与△KFO③△NQP与△NMQ.其中，互为顺相似的是 ；互为逆相似的是 。（填写所有符合要求的序号）‎ ‎(2)如图③在锐角△ABC中，∠A＜∠B＜∠C，点P在△ABC的边上（不与A、B、C重合）过点P画直线截△ABC，使截得的一个三角形与△ABC互为逆相似，请根据点P的不同位置，探究过点P的截线的情形，画出图形并说明截线满足的条件，不必说明理由。‎