2021年九 年级中考数学全程复习专题七：解直角三角形的实际应用的基本类型 课件

2021年九 年级中考数学全程复习专题七：解直角三角形的实际应用的基本类型 课件

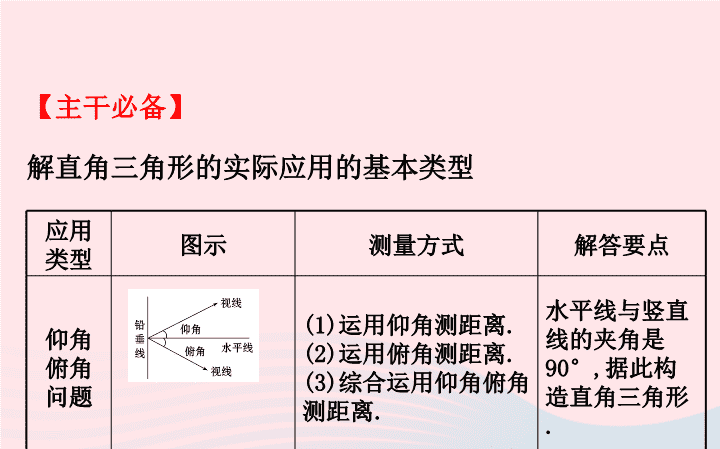
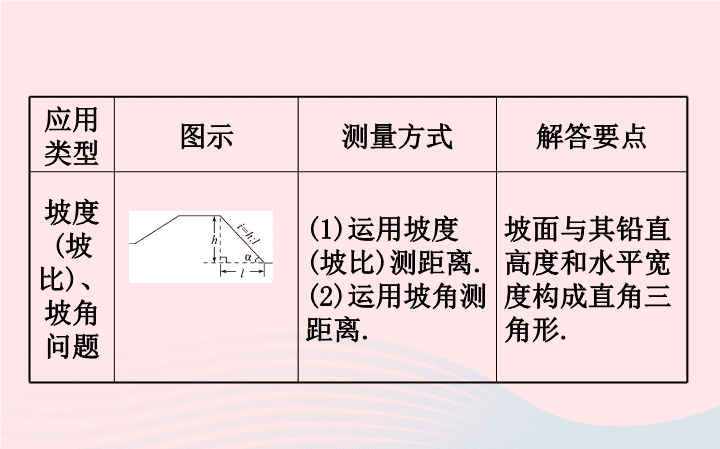
微专题七　 解直角三角形的实际 应用的基本类型 【主干必备】 解直角三角形的实际应用的基本类型 应用 类型 图示 测量方式 解答要点 仰角 俯角 问题 (1)运用仰角测距离. (2)运用俯角测距离. (3)综合运用仰角俯 角测距离. 水平线与竖直 线的夹角是 90°,据此构 造直角三角形. 应用 类型 图示 测量方式 解答要点 坡度 (坡 比)、 坡角 问题 (1)运用坡度 (坡比)测距离. (2)运用坡角测 距离. 坡面与其铅直 高度和水平宽 度构成直角三 角形. 应用 类型 图示 测量方式 解答要点 方位 角问 题 一般根据两 个方位角测 距离. 通过向南北 (东西)方向 作垂线,或向 航线作垂线, 构造直角三 角形. 【微点警示】 除以上三种比较典型的问题外,解直角三角形的实际应 用还有多种形式,体现在生产、生活的方方面面,它们 共同的特点就是利用直角三角形测距离. 【核心突破】 【类型一】 仰角俯角问题 例1(2019·天津中考)如图,海面上一艘 船由西向东航行,在A处测得正东方向上 一座灯塔的最高点C的仰角为31°,再向东继续航行30 m 到达B处,测得该灯塔的最高点C的仰角为45°,根据测 得的数据,计算这座灯塔的高度CD(结果取整数). 参考数据:sin 31°≈0.52,cos 31°≈0.86, tan 31°≈0.60. 【思路点拨】根据正切的定义用CD表示出AD,根据题意 列出方程,解方程得到答案. 【自主解答】 在Rt△CAD中,tan∠CAD= , 则AD= , 在Rt△CBD中,∠CBD=45°,∴BD=CD, ∵AD=AB+BD,∴ CD=30+CD, CD AD CD 5 CDtan31 3  5 3 解得,CD=45. 答:这座灯塔的高度CD约为45 m. 【类型二】 坡度(坡比)、坡角问题 例2(2018·泰州中考)日照间距系数反 映了房屋日照情况.如图①,当前后房 屋都朝向正南时,日照间距系数=L∶ (H-H1),其中L为楼间水平距离,H为南侧楼房高度,H1为 北侧楼房底层窗台至地面高度. 如图②,山坡EF朝北,EF长为15 m,坡度为i=1∶0.75,山 坡顶部平地EM上有一高为22.5 m的楼房AB,底部A到E点 的距离为4 m. (1)求山坡EF的水平宽度FH. (2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知 该楼底层窗台P处至地面C处的高度为0.9 m,要使该楼 的日照间距系数不低于1.25,底部C距F处至少多远? 【思路点拨】(1)在Rt△EFH中,根据坡度的定义及EF的 长求山坡EF的水平宽度FH. (2)根据该楼的日照间距系数不低于1.25,列出不等式, 解不等式即可. 【自主解答】 (1)略 (2)∵L=CF+FH+EA=CF+9+4=(CF+13) m, H=AB+EH=22.5+12=34.5(m),H1=0.9 m, ∴日照间距系数=L∶(H-H1)= CF 13 CF 13 34.5 0.9 33.6    ＝ ， ∵该楼的日照间距系数不低于1.25, ∴ ≥1.25,∴CF≥29. 答:要使该楼的日照间距系数不低于1.25,底部C距F处 至少29 m远. CF 13 33.6  【类型三】方位角问题 例3(2019·怀化中考)如图,为测量 一段笔直自西向东的河流的河面宽 度,小明在南岸B处测得对岸A处一 棵柳树位于北偏东60°方向,他以每秒1.5米的速度沿 着河岸向东步行40秒后到达C处,此时测得柳树位于北 偏东30°方向,试计算此段河面的宽度. 【思路点拨】作AD⊥BC于点D.由题意得到BC=1.5× 40=60米,∠ABD=30°,∠ACD=60°,根据三角形的外角 的性质得到∠BAC=∠ACD-∠ABC=30°,求得∠ABC= ∠BAC,得到BC=AC=60米.在Rt△ACD中,根据三角函数的 定义即可得到结论. 【自主解答】 略 【明·技法】 解直角三角形实际应用的“两个注意” (1)注意有无直角:图形中有直角要充分利用,无直角作 辅助线构造直角. (2)注意是否可解:分析直角三角形的边角条件,若已知 一边一角或两边,可直接解之;若边角条件不充分,一般 需设未知数列方程. 【题组过关】 1.(2019·来宾模拟)河堤横断面 如图所示,堤高BC=6 m,迎水坡AB 的坡比为1∶ ,则AB的长为 (　 　) A.12 m　　B.4 m　　C.5 m　　D.6 m 3 3 3 3 A 2.(2019·益阳中考)南洞庭大桥是南益 高速公路上的重要桥梁,小芳同学在校 外实践活动中对此开展测量活动.如 图,在桥外一点A测得大桥主架与水面的交汇点C的俯角 为α,大桥主架的顶端D的仰角为β,已知测量点与大桥 主架的水平距离AB=a,则此时大桥主架顶端离水面的高 CD为 (　 　) A.asinα+asinβ　　　　B.acosα+acosβ C.atanα+atanβ D. C a a tan tan   3.(2019·泰安中考)如图,一艘船由 A港沿北偏东65°方向航行30 km 至B港,然后再沿北偏西40°方向航 行至C港,C港在A港北偏东20°方向, 则A,C两港之间的距离为_________km. 2 B 世纪金榜导学号(　 　)  A.30+30 　　　　　　 B.30+10 C.10+30 D.30 3 3 3 3 4.(2019·荆州中考)如图,灯塔A在测 绘船的正北方向,灯塔B在测绘船的东 北方向,测绘船向正东方向航行20海 里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘 船北偏西63.5°的方向上,则灯塔A,B间的距离为 _________海里(结果保留整数).(参考数据sin 26.5° ≈0.45,cos 26.5°≈0.90,tan 26.5°≈0.50, ≈ 2.24)  22 5 5.(2019·上海宝山区模拟)地铁10 号线某站点出口横截面平面图如图 所示,电梯AB的两端分别距顶部9.9 米和2.4米,在距电梯起点A端6米的P处,用1.5米高的测 角仪测得电梯终端B处的仰角为14°,求电梯AB的坡度 与长度. 参考数据:sin 14°≈0.24,tan 14°≈0.25, cos 14°≈0.97. 世纪金榜导学号 【解析】作BC⊥PA交PA的延长线于点C,作QD∥PC交BC 于点D. 由题意可得,BC=9.9-2.4=7.5(米),QP=DC=1.5米, ∠BQD=14°, 则BD=BC-DC=7.5-1.5=6(米). ∵tan ∠BQD= , ∴tan 14°= ,即0.25= , BD QD 6 6 ED 6 6 ED 解得,ED=18, ∴AC=ED=18米. ∵BC=7.5米, ∴tan ∠BAC= . ∵BC=7.5米,AC=18米,∠BCA=90°, BC 7.5 5 AC 18 12 ＝ ∴AB= =19.5(米), 即电梯AB的坡度是5∶12,长度是19.5米. 2 27.5 18