- 2021-11-12 发布 |
- 37.5 KB |
- 3页
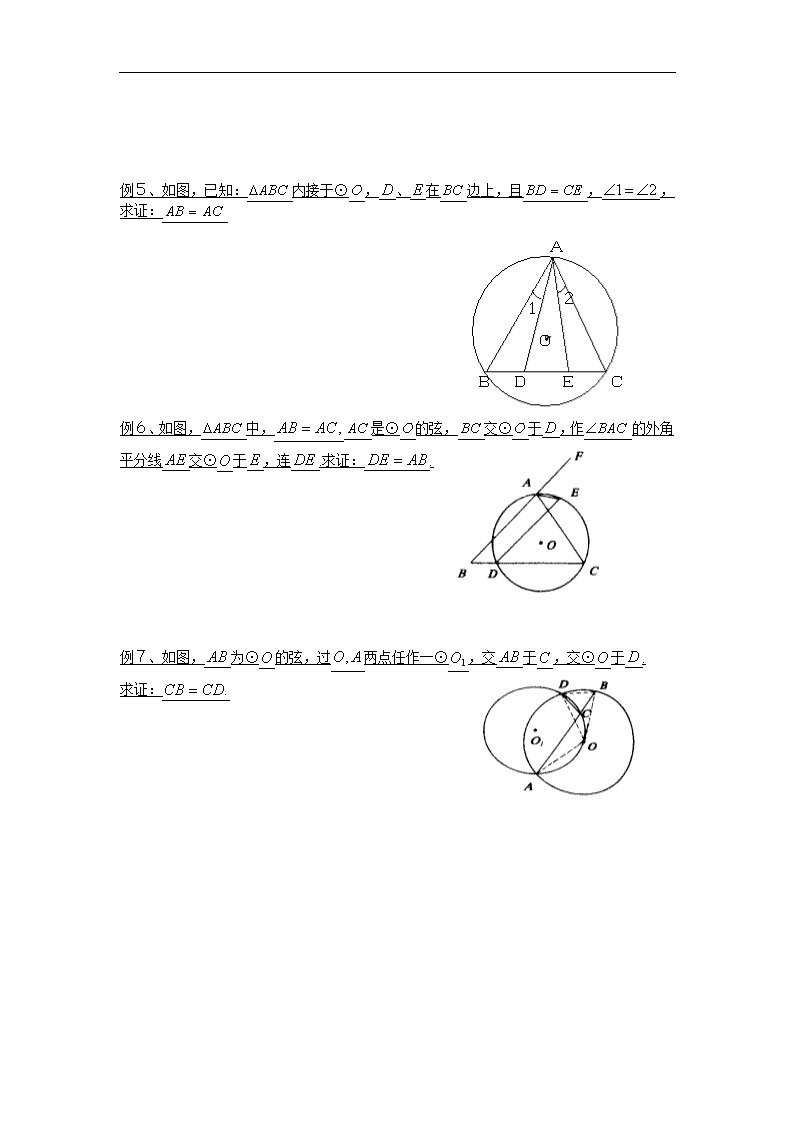
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学专题复习练习:圆周角定理内容
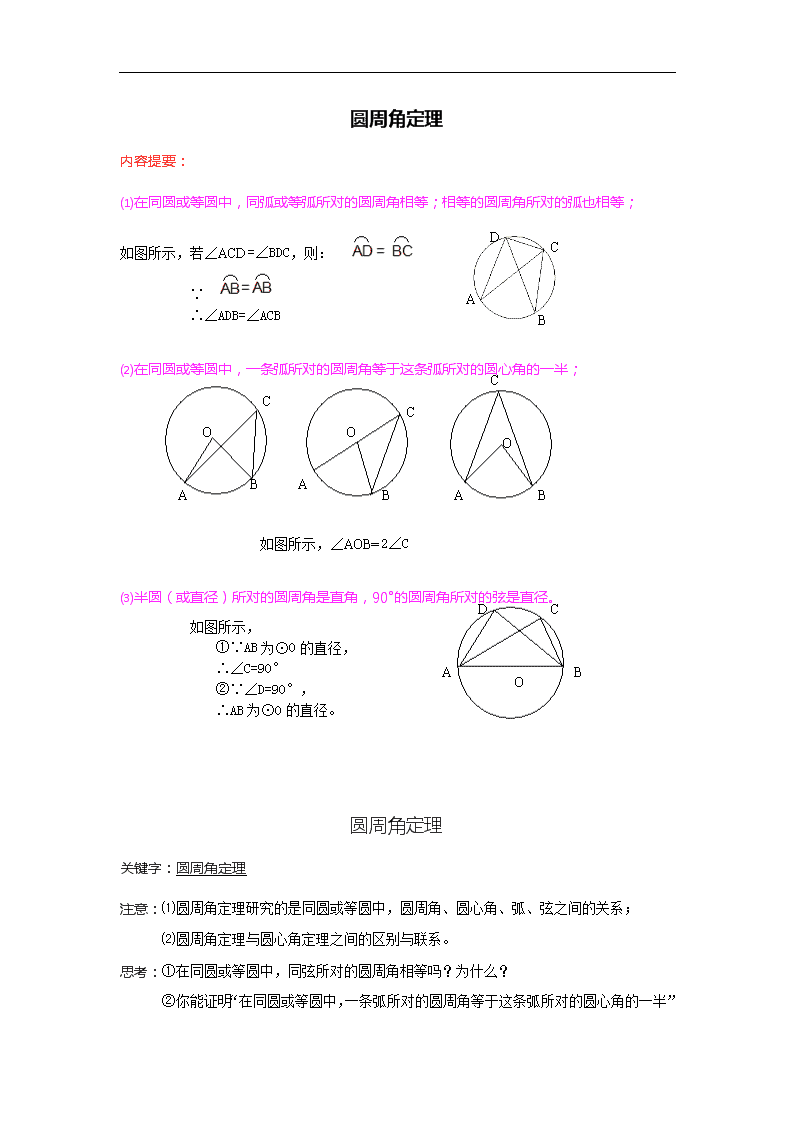
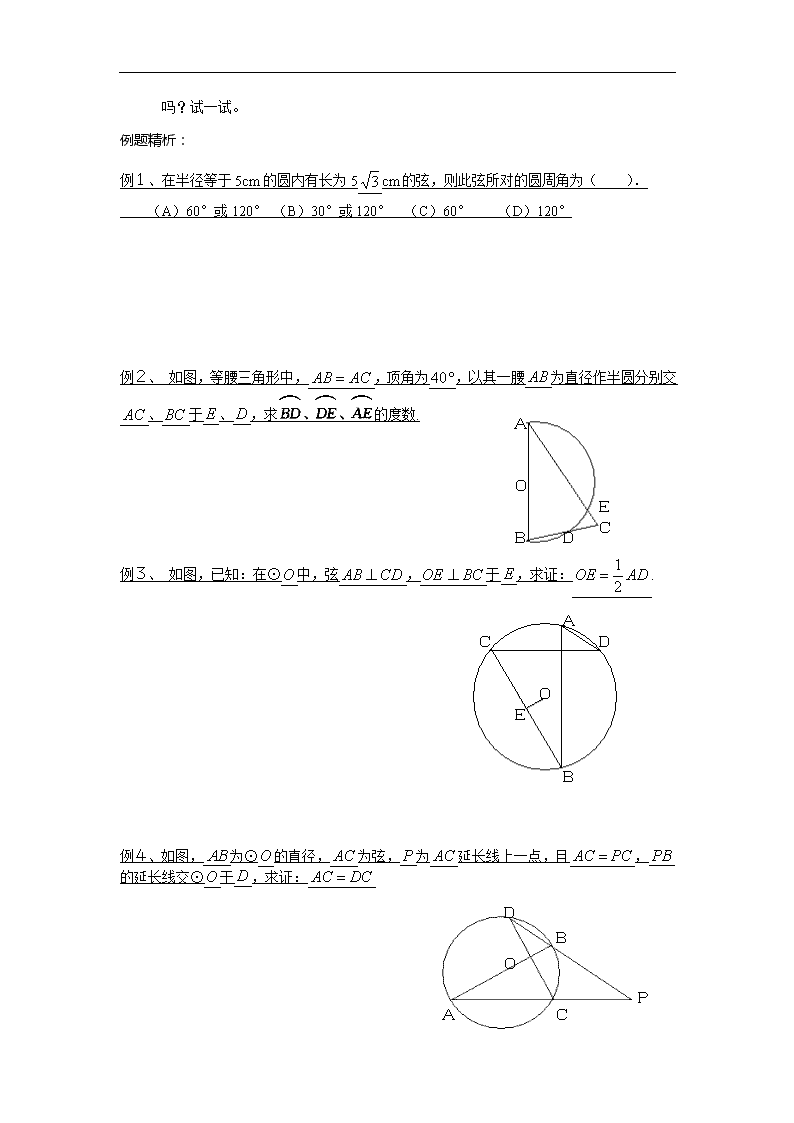
圆周角定理 内容提要: ⑴在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等; B A D C 如图所示,若∠ACD=∠BDC,则: ∵ ∴∠ADB=∠ACB A A A C C C O O O B B B ⑵在同圆或等圆中,一条弧所对的圆周角等于这条弧所对的圆心角的一半; 如图所示,∠AOB=2∠C A B C D O ⑶半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。 如图所示, ①∵AB为⊙O的直径, ∴∠C=90° ②∵∠D=90°, ∴AB为⊙O的直径。 圆周角定理 关键字:圆周角定理 注意:⑴圆周角定理研究的是同圆或等圆中,圆周角、圆心角、弧、弦之间的关系; ⑵圆周角定理与圆心角定理之间的区别与联系。 思考:①在同圆或等圆中,同弦所对的圆周角相等吗?为什么? ②你能证明“在同圆或等圆中,一条弧所对的圆周角等于这条弧所对的圆心角的一半” 吗?试一试。 例题精析: 例1、在半径等于5cm的圆内有长为5cm的弦,则此弦所对的圆周角为( ). (A)60°或120° (B)30°或120° (C)60° (D)120° A A B C D E O 例2、 如图,等腰三角形中,,顶角为,以其一腰为直径作半圆分别交、于、,求的度数. C D A B E O 例3、 如图,已知:在⊙中,弦,于,求证:. A A B P C D O 例4、如图,为⊙的直径,为弦,为延长线上一点,且,的延长线交⊙于,求证: A B C D E O 1 2 例5、如图,已知:内接于⊙,、在边上,且,,求证: 例6、如图,中,是⊙的弦,交⊙于,作的外角平分线交⊙于,连.求证:. 例7、如图,为⊙的弦,过两点任作一⊙,交于,交⊙于. 求证:查看更多