2020年湖南省岳阳市中考数学试卷【含答案;word版本试题;可编辑】
2020年湖南省岳阳市中考数学试卷
一、选择题(本大题共8小题,每小题3分,满分24分,在每道小题给出的四个选项中,选出符合要求的一项)
1. -2020的相反数是( )
A.-2020 B.2020 C.-12020 D.12020
2. 2019年以来,我国扶贫攻坚取得关键进展,农村贫困人口减少11090000人,数据11090000用科学记数法表示为( )
A.0.1109×108 B.11.09×106 C.1.109×108 D.1.109×107
3. 如图,由4个相同正方体组成的几何体,它的左视图是( )
A. B. C. D.
4. 下列运算结果正确的是( )
A.(-a)3=a3 B.a9÷a3=a3 C.a+2a=3a D.a⋅a2=a2
5. 如图,DA⊥AB,CD⊥DA,∠B=56∘,则∠C的度数是( )
A.154∘ B.144∘ C.134∘ D.124∘
6. 今年端午小长假复课第一天,学校根据XX防控要求,对所有进入校园的师生进行体温检测,其中7名学生的体温(单位:∘C)如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数和中位数分别是( )
A.36.3,36.5 B.36.5,36.5 C.36.5,36.3 D.36.3,36.7
7. 下列命题是真命题的是( )
A.一个角的补角一定大于这个角
B.平行于同一条直线的两条直线平行
C.等边三角形是中心对称图形
D.旋转改变图形的形状和大小
8. 对于一个函数,自变量x取c时,函数值y等于0,则称c为这个函数的零点.若关于x的二次函数y=-x2-10x+m(m≠0)有两个不相等的零点x1,x2(x1
1 C.01
二、填空题(本大题共8个小题,每小题4分,满分32分)
9. 因式分解:a2-9=________.
10. 函数y=x-2中,自变量x的取值范围是________.
11. 不等式组x+3≥0,x-1<0 的解集是________.
12. 如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20∘,则∠BCD=________∘.
13. 已知x2+2x=-1,则代数式5+x(x+2)的值为________.
14. 我国古代数学名著《九章算术》上有这样一个问题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其大意是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现用30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,根据题意,可列方程组为________.
15. 如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O
9 / 9
相切于点B.点P为AM上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是________.
①PB=PD;②BC的长为43π;③∠DBE=45∘;④△BCF∽△PFB;⑤CF⋅CP为定值.
三、解答题(本大题共8小题,满分64分,解答应写出必要的文字说明、证明过程或演算步骤)
16. 计算:(12)-1+2cos60∘-(4-π)0+|-3|.
17. 如图,点E,F在▱ABCD的边BC,AD上,BE=13BC,FD=13AD,连接BF,DE.
求证:四边形BEDF是平行四边形.
18. 如图,一次函数y=x+5的图象与反比例函数y=kx(k为常数且k≠0)的图象相交于A(-1, m),B两点.
(1)求反比例函数的表达式;
(2)将一次函数y=x+5的图象沿y轴向下平移b个单位(b>0),使平移后的图象与反比例函数y=kx的图象有且只有一个交点,求b的值.
9 / 9
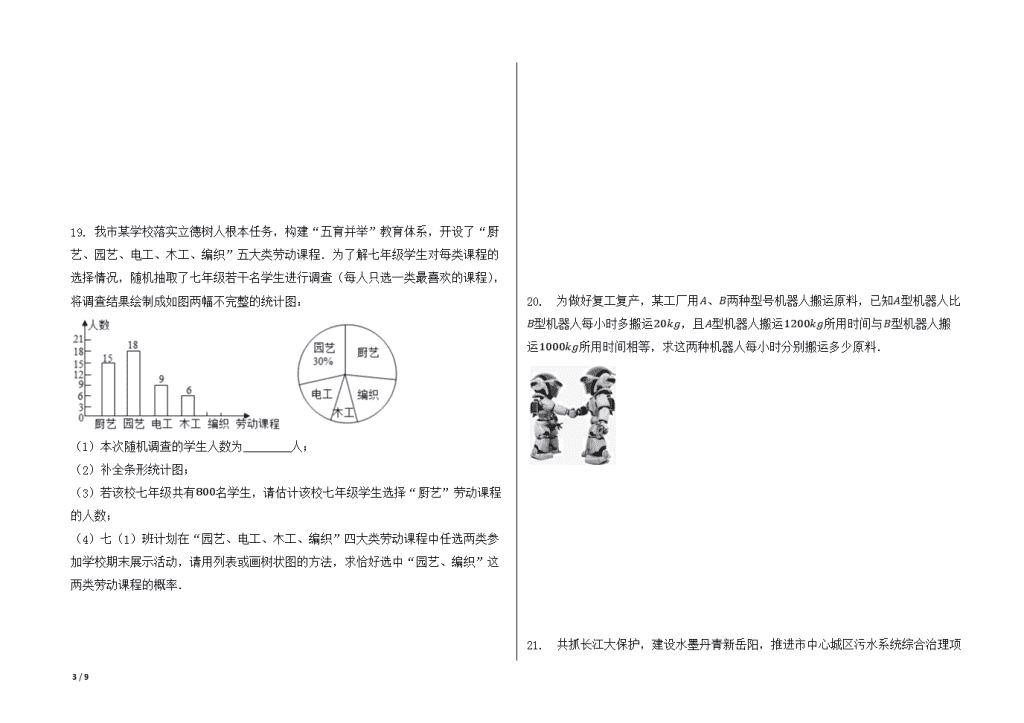
19. 我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如图两幅不完整的统计图:
(1)本次随机调查的学生人数为________人;
(2)补全条形统计图;
(3)若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;
(4)七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.
20. 为做好复工复产,某工厂用A、B两种型号机器人搬运原料,已知A型机器人比B型机器人每小时多搬运20kg,且A型机器人搬运1200kg所用时间与B型机器人搬运1000kg所用时间相等,求这两种机器人每小时分别搬运多少原料.
21.
9 / 9
共抓长江大保护,建设水墨丹青新岳阳,推进市中心城区污水系统综合治理项目,需要从如图A,B两地向C地新建AC,BC两条笔直的污水收集管道,现测得C地在A地北偏东45∘方向上,在B地北偏西68∘向上,AB的距离为7km,求新建管道的总长度.(结果精确到0.1km,sin22∘≈0.37,cos22∘≈0.93,tan22∘≈0.40,2≈1.41)
22. 如图1,在矩形ABCD中,AB=6,BC=8,动点P,Q分别从C点,A点同时以每秒1个单位长度的速度出发,且分别在边CA,AB上沿C→A,A→B的方向运动,当点Q运动到点B时,P,Q两点同时停止运动.设点P运动的时间为t(s),连接PQ,过点P作PE⊥PQ,PE与边BC相交于点E,连接QE.
(1)如图2,当t=5s时,延长EP交边AD于点F.求证:AF=CE;
(2)在(1)的条件下,试探究线段AQ,QE,CE三者之间的等量关系,并加以证明;
(3)如图3,当t>94s时,延长EP交边AD于点F,连接FQ,若FQ平分∠AFP,求AFCE的值.
9 / 9
23. 如图1所示,在平面直角坐标系中,抛物线F1:y=a(x-25)2+6415与x轴交于点A(-65, 0)和点B,与y轴交于点C.
(1)求抛物线F1的表达式;
(2)如图2,将抛物线F1先向左平移1个单位,再向下平移3个单位,得到抛物线F2,若抛物线F1与抛物线F2相交于点D,连接BD,CD,BC.
①求点D的坐标;
②判断△BCD的形状,并说明理由;
(3)在(2)的条件下,抛物线F2上是否存在点P,使得△BDP为等腰直角三角形,若存在,求出点P的坐标;若不存在,请说明理由.
9 / 9
参考答案与试题解析
2020年湖南省岳阳市中考数学试卷
一、选择题(本大题共8小题,每小题3分,满分24分,在每道小题给出的四个选项中,选出符合要求的一项)
1.B
2.D
3.A
4.C
5.D
6.B
7.B
8.A
二、填空题(本大题共8个小题,每小题4分,满分32分)
9.(a+3)(a-3)
10.x≥2
11.-3≤x<1
12.70
13.4
14.x+y=250x+10y=30
15.②⑤
三、解答题(本大题共8小题,满分64分,解答应写出必要的文字说明、证明过程或演算步骤)
16.原式=2+2×12-1+3
=2+1-1+3
=2+3.
17.∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD // BC,
∵ BE=13BC,FD=13AD,
∴ BE=DF,
∵ DF // BE,
∴ 四边形BEDF是平行四边形.
18.∵ 一次函数y=x+5的图象与反比例函数y=kx(k为常数且k≠0)的图象相交于A(-1, m),
∴ m=4,
∴ k=-1×4=-4,
∴ 反比例函数解析式为:y=-4x;
∵ 一次函数y=x+5的图象沿y轴向下平移b个单位(b>0),
∴ y=x+5-b,
∵ 平移后的图象与反比例函数y=kx的图象有且只有一个交点,
∴ x+5-b=-4x,
∴ x2+(5-b)x+4=0,
∵ △=(5-b)2-16=0,
解得b=9或1,
答:b的值为9或1.
19.60
60-15-18-9-6=12(人),补全条形统计图如图所示:
9 / 9
800×1560=200(人),
答:该校七年级800名学生中选择“厨艺”劳动课程的有200人;
用列表法表示所有可能出现的结果如下:
共有12种可能出现的结果,其中选中“园艺、编织”的有2种,
∴ P(园艺、编织)=212=16.
20.A型机器人每小时搬运120kg原料,B型机器人每小时搬运100kg原料
21.新建管道的总长度约为8.2km
22.∵ 四边形ABCD是矩形,
∴ AD // BC,∠ABC=90∘,
在Rt△ABC中,AB=6,BC=8,根据勾股定理得,AC=10,
由运动知,CP=t=5,
∴ AP=AC-CP=5,
∴ AP=CP,
∵ AD // BC,
∴ ∠PAF=∠PCE,∠AFP=∠CEP,
∴ △APF≅△CPE(AAS),
∴ AF=CE;
结论:AQ2+CE2=QE2,
理由:如图2,
连接FQ,由(1)知,△APF≅△CPE,
∴ AF=CE,PE=PF,
∵ EF⊥PQ,
∴ QE=QF,
在Rt△QAF中,根据勾股定理得,AQ2+AF2=QF2,
∴ AQ2+CE2=QE2;
如图3,
由运动知,AQ=t,CP=t,
∴ AP=AC-CP=10-t,
∵ FQ平分∠AFE,
∴ ∠AFQ=∠PFQ,
∵ ∠FAQ=∠FPQ=90∘,FQ=FQ,
∴ △FAQ≅△FPQ(AAS),
∴ AQ=PQ=t,AF=PF,
∴ BQ=AB-AQ=6-t,∠FAC=∠FPA,
∵ ∠DAC=∠ACB,∠APF=∠CPE,
∴ ∠ACB=∠CPE,
∴ PE=CE,过点E作EN⊥AC于N,
∴ CN=12CP=12t,∠CNE=90∘=∠ABC,
∵ ∠NCE=∠BCA,
∴ △CNE∽△CBA,
9 / 9
∴ CEAC=CNCB,
∴ CE10=12t8,
∴ CE=58t,
∴ PE=58t,BE=BC-CE=8-58t,
在Rt△QPE中,QE2=PQ2+PE2,
在Rt△BQE中,QE2=BQ2+BE2,
∴ PQ2+PE2=BQ2+BE2,
∴ t2+(58t)2=(6-t)2+(8-58t)2,
∴ t=5011,
∴ CP=t=5011,
∴ AP=10-CP=6011,
∵ AD // BC,
∴ △APF∽△CPE,
∴ AFCE=APCP=60115011=65.
23.把点A(-65, 0)代入抛物线F1:y=a(x-25)2+6415中得:
0=a(-65-25)2+6415,
解得:a=-53,
∴ 抛物线F1:y=-53(x-25)2+6415;
①由平移得:抛物线F2:y=-53(x-25+1)2+6415-3,
∴ y=-53(x+35)2+1915,
∴ 53(x+35)2+1915=-53(x-25)2+6415,
-103x=103,
解得:x=-1,
∴ D(-1, 1);
②当x=0时,y=-53×425+6415=4,
∴ C(0, 4),
当y=0时,-53(x-25)2+6415=0,
解得:x=-65或2,
∴ B(2, 0),
∵ D(-1, 1),
∴ BD2=(2+1)2+(1-0)2=10,
CD2=(0+1)2+(4-1)2=10,
9 / 9
BC2=22+42=20,
∴ BD2+CD2=BC2且BD=CD,
∴ △BDC是等腰直角三角形;
存在,
设P(m, -53(m+35)2+1915),
∵ B(2, 0),D(-1, 1),
∴ BD2=(2+1)2+12=10,PB2=(m-2)2+[-53(m+35)2+1915]2,PD2=(m+1)2+[-53(m+35)2+1915-1]2,
分三种情况:
①当∠DBP=90∘时,BD2+PB2=PD2,
即10+(m-2)2+[-53(m+35)2+1915]2=(m+1)2+[-53(m+35)2+1915-1]2,
解得:m=-4或1,
当m=-4时,BD=10,PB=36+324=610,即△BDP不是等腰直角三角形,不符合题意,
当m=1时,BD=10,PB=1+9=10,
∴ BD=PB,即△BDP是等腰直角三角形,符合题意,
∴ P(1, -3);
②当∠BDP=90∘时,BD2+PD2=PB2,
即10+[-53(m+35)2+1915-1]2=(m-2)2+[-53(m+35)2+1915]2,
解得:m=-1(舍)或-2,
当m=-2时,BD=10,PD=1+9=10,
∴ BD=PD,即此时△BDP为等腰直角三角形,
∴ P(-2, -2);
③当∠BPD=90∘时,且BP=DP,有BD2=PD2+PB2,如图3,
当△BDP为等腰直角三角形时,点P1和P2不在抛物线上,此种情况不存在这样的点P;
综上,点P的坐标是(1, -3)或(-2, -2).
9 / 9