九年级数学下册第一章直角三角形的边角关系1从梯子的倾斜程度谈起第2课时习题课件北师大版

九年级数学下册第一章直角三角形的边角关系1从梯子的倾斜程度谈起第2课时习题课件北师大版

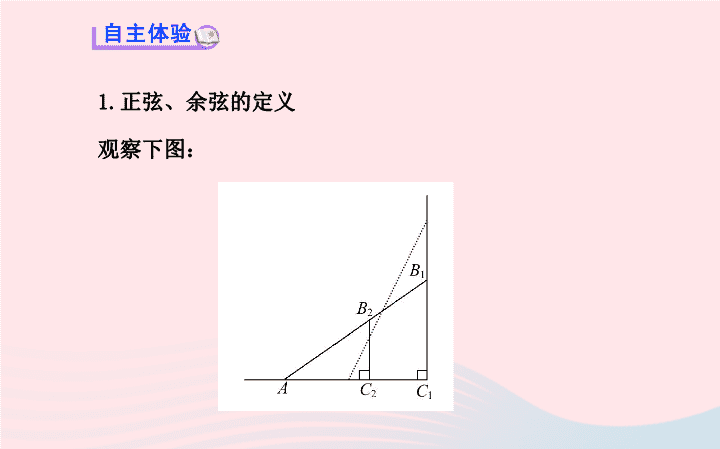
1 从梯子的倾斜程度谈起 第 2 课时 1. 理解正弦和余弦的意义 , 能够运用 sin A ， cos A 表示直角三角形两边的比 .( 重点 ) 2. 能根据直角三角形中的边角关系，进行简单的计算 .( 重点 ) 3. 用函数的观点理解正弦、余弦和正切 .( 难点 ) 1. 正弦、余弦的定义 观察下图： 【 思考 】 ( 1)△AB 1 C 1 和△ AB 2 C 2 相似吗？为什么？ 提示： 相似，∵∠ A=∠A,∠AC 1 B 1 =∠AC 2 B 2 =90° ， ∴△ AB 1 C 1 ∽△AB 2 C 2 . (2) 吗？ 吗？为什么？ 提示： 由相似三角形的对应边成比例 可知它们成立 . (3) 如果改变 B 2 在 AB 1 上的位置或改变 AB 1 的倾斜角的大小，上 述结论 _____( 填“成立”或“不成立” ). 成立 (4) 梯子的倾斜程度与上面的比值有何关系？ 提示： 的比值越大，梯子越陡； 的比 值越小，梯子越陡 . 【 总结 】 (1) 正弦、余弦的定义： 在 Rt△ABC 中，如果锐角 A 确定，那么∠ A 的 _____ 与 _____ 的比 也随之确定，这个比叫做∠ A 的正弦，记作 _______ ；∠ A 的 _____ 与 _____ 的比也随之确定，这个比叫做∠ A 的余弦，记作 ______ . 对边 斜边 sin A 邻边 斜边 cos A (2) 梯子的倾斜程度与正弦、余弦的关系： 如果梯子与地面的夹角为∠ A ，那么 sin A 的值 _____ ，梯子 越陡； cos A 的值 _____ ，梯子越陡 . 越大 越小 2. 锐角三角函数的定义 . 锐角 A 的 _____ 、 _____ 和 _____ 都是∠ A 的三角函数 . 正弦 余弦 正切 ( 打“√”或“ ×”) (1) 一个锐角的三角函数值一定小于 1.( ) (2) 一个锐角的正弦值大于这个角的余弦值 .( ) (3) 任何一个锐角都有其对应的三角函数值 .( ) (4) 一个锐角的三角函数值确定，那么这个锐角也确定 .( ) (5)sin A 表示 sin 与 A 的乘积 .( ) (6) 在 Rt△ABC 中，∠ C=90°, 则 ( ) × × √ √ × √ 知识点 1 锐角三角函数的求值 【 例 1】 已知：如图，在△ ABC 中，∠ C ＝ 90° ，点 D ， E 分 别在边 AB ， AC 上， DE∥BC ， DE ＝ 3 ， BC ＝ 9. (1) 求 的值 . (2) 若 BD ＝ 10 ，求 sin A 的值． 【 解题探究 】 (1)①△AED 与△ ACB 相似吗？为什么？ 提示： 相似 .∵DE∥BC ， ∴∠ AED=∠C ，∠ ADE=∠B ， ∴△ AED∽△ACB. ② 根据上面的探究，如何求出 的值？ 提示： (2)① 因为△ ABC 中，∠ C ＝ 90° ， BC=9 ，所以要求 sin A 的值，需要知道哪条线段的长？ 提示： 需要知道 AB 的长 . ② 请求出①中要求线段的长是多少？ 提示： ∴ AB=AD+BD=5+10=15. 根据上面的探究可知 【 互动探究 】 在上面的问题中，求 sin A 的值时，还可以把∠ A 放在哪个三角形中？为什么？ 提示： 可以把∠ A 放在△ ADE 中，因为∠ AED=∠C=90° ， DE ＝ 3 ，且能求出 AD 的长 . 【 总结提升 】 利用定义求锐角三角函数值的三点注意 1. 必须在直角三角形中求解 . 2. 并不是只有直角三角形中的角才有三角函数值，任何一个锐角都有其对应的三角函数值，若锐角所在的三角形不是直角三角形，应先构造直角三角形，再求出相应角的三角函数值 . 3. 锐角三角函数值是两条边的比，没有单位 . 知识点 2 锐角三角函数的应用 【 例 2】 如图，在 Rt△ABC 中，∠ ACB=90° ，已知 CD⊥AB ， CD=8 ，如果 求 AB 的长． 【 思路点拨 】 先在 Rt△BDC 中，由 求出 BC 的长， 再在 Rt△ABC 中，由 求出 AB 的长 . 【 自主解答 】 在 Rt△BDC 中， ∴设 BD=3x ，则 BC=5x ， 在△ BCD 中，由勾股定理得： BD 2 +CD 2 =BC 2 , 即 (3x) 2 +8 2 =(5x) 2 ，解得 x 1 =2 ， x 2 =-2( 舍去 ) ， ∴ BC=5x=10. ∵∠A+∠ACD=90° ，∠ BCD+∠ACD=90° ， ∴∠ A=∠BCD ， ∴在 Rt△ABC 中， 【 总结提升 】 锐角三角函数的两个应用和两点注意 两个应用： (1) 已知一个锐角的三角函数值，求直角三角形的边长或两条边的比 . (2) 已知一个锐角的某一个三角函数值，求这个锐角的其他三角函数值 . 两点注意： (1) 锐角三角函数值都是正数，且都揭示了直角三角形的边角关系 . (2) 锐角三角函数经常与勾股定理结合使用 . 题组一： 锐角三角函数的求值 1.(2013· 温州中考 ) 如图，在△ ABC 中，∠ C=90° ， AB=5 ， BC=3 ，则 sin A 的值是 ( ) 【 解析 】 选 C. 【 变式备选 】 (2013· 广东中考 ) 在 Rt△ABC 中 ,∠ABC=90°, AB=3,BC=4, 则 sin A=______. 【 解析 】 ∵∠ABC=90° ， AB=3 ， BC=4 ， 答案： 2. 如图，在 Rt△ABC 中，∠ C ＝ 90° ， AB ＝ 2BC ，则 sin B 的 值为 ( ) 【 解析 】 选 C ．设 BC=m ，则 AB=2m ，根据勾股定理得 AC= 3. 在平面直角坐标系 xOy 中，已知点 A(2 ， 1) 和点 B(3 ， 0) ， 则 sin∠AOB 的值等于 ( ) 【 解析 】 选 A. 如图，根据勾股定理得， 则 4.(2013· 湖州中考 ) 如图，已知在 Rt△ACB 中，∠ C=90° ， AB=13 ， AC=12 ，则 cos B 的值为 ______ ． 【 解析 】 ∵Rt△ACB 中，∠ C=90° ， AB=13 ， AC=12 ， 答案： 5. 已知：如图，在梯形 ABCD 中， AD∥BC ，∠ D=90° ， AD∶AB=2∶5 ， AB=BC ，求 sin B ． 【 解析 】 如图，过 A 作 AE⊥BC 于 E ， 则∠ AEB=∠AEC=90° ． ∵ AD∶AB=2∶5 ， AB=BC ， ∴设 AD=2k ， 则 AB=BC=5k(k ＞ 0) ． ∵ 在梯形 ABCD 中， AD∥BC ，∠ D=90° ， ∴∠ C=180°-∠D=90° ． ∴∠ D=∠C=∠AEC=90° ． ∴四边形 AECD 是矩形． ∴ CE=AD=2k ．∴ BE=BC-CE=3k ， 在 Rt△AEB 中，由勾股定理得： (5k) 2 -(3k) 2 =AE 2 , 解得： AE=4k ． 题组二： 锐角三角函数的应用 1.(2013· 杭州中考 ) 在 Rt△ABC 中，∠ C=90° ，若 AB=4 ， 则斜边上的高等于 ( ) 【 解析 】 选 B. 通过 可得出 如图，过点 C 作 AB 边的垂线交 AB 边于点 D ，则根据 sin B= 得出 2. 如图，△ ABC 中， 则△ ABC 的面 积是 ( ) 【 解析 】 选 A. 作 AD⊥BC, 又 设 则 AB=2x ， ∵ AB 2 =BD 2 +AD 2 ,∴4x 2 =2x 2 +9 ， ( 舍去 ).∴BD=3, 3. 把△ ABC 三边的长度都扩大为原来的 3 倍，则锐角 A 的正弦函 数值 ( ) A ．不变 B ．缩小为原来的 C ．扩大为原来的 3 倍 D ．不能确定 【 解析 】 选 A. 设三边长度扩大前 则三边长度扩大后 的正弦值为 即三边长度扩大前后 sin A 的值不变 . 4.(2013· 鞍山中考 )△ABC 中， 则 BC 的长为 ______ ． 【 解析 】 ∵ 答案： 【 变式备选 】 在△ ABC 中 , 则 AC 的长 为 ( ) A.6 B.4 C. D. 【 解析 】 选 B. 5. 如图，在 Rt△ABC 中，∠ C=90° ， D 是 BC 边上一点， AC=2 ， CD=1 ，设∠ CAD=α ． (1) 求 sin α,cos α,tan α 的值 . (2) 若∠ B=∠CAD ，求 BD 的长． 【 解析 】 在 Rt△ACD 中， (1) (2) 在 Rt△ABC 中，∵∠ B=∠CAD=α, ∴BD=BC-CD=4-1=3. 【 想一想错在哪？ 】 在 Rt△ABC 中， AC=3 ， BC=4 ，求 sin A 的 值 . 提示 : 漏掉了 BC 为斜边 ,∠A 为直角的情况 !