2010中考数学红河考试试题

2010中考数学红河考试试题

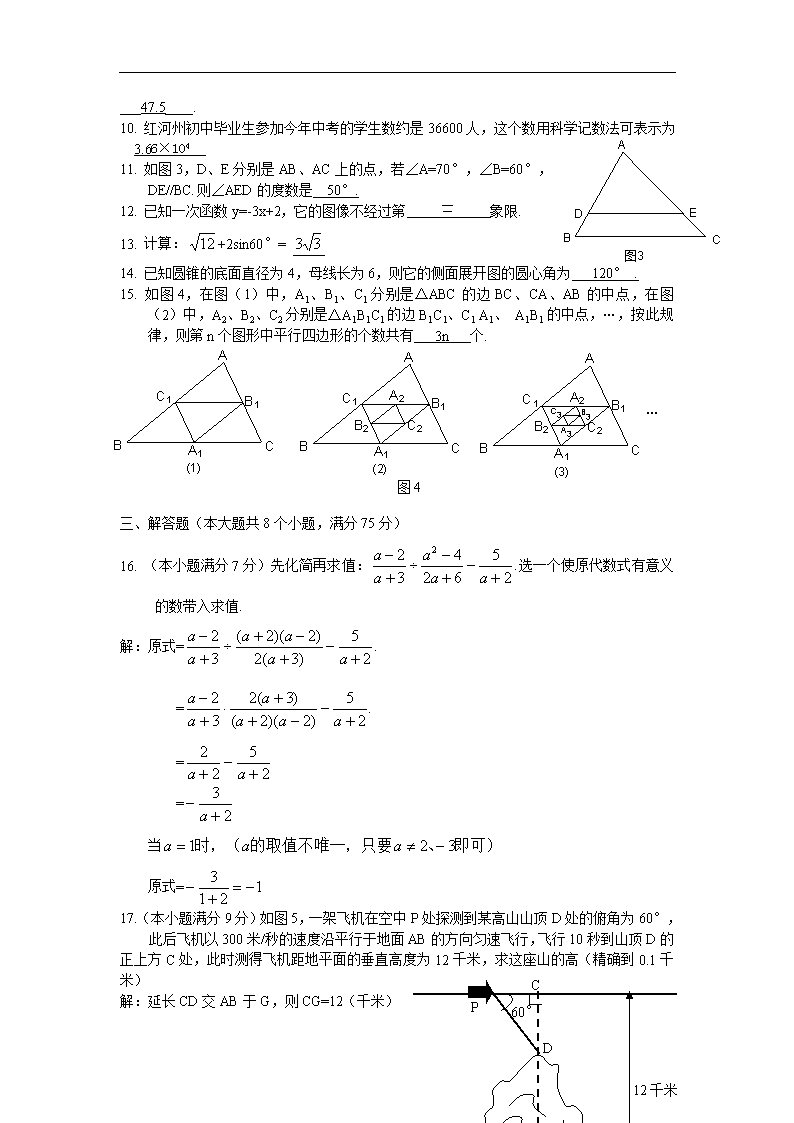
哈尼族 彝 族 红河 自治州2010年高中（中专）招生统一考试 数学试卷 一、 选择题（本大题共7个小题，每小题只有一个选项符合题目要求，每小题3分，满分21分）‎ 1. 下列计算正确的是 （ C ）‎ A．（-1）-1=1 B.（-3）2=-6 C.π0=1 D.（-2）6÷（-2）3=（-2）2‎ 2. 不在函数图像上的点是 （ D ）‎ A．（2,6） B.（-2，-6） C.（3,4） D.（-3,4）‎ 3. 图1是由大小相同的5个小正方体搭成的几何体，则它的主视图是 （ B ）‎ ‎ ‎ 图1‎ 4. 使分式有意义的x的取值是 （ D ） ‎ A.x≠0 B. x≠±3 C. x≠-3 D. x≠3‎ ‎ ‎ 5. 下列命题错误的是 （ B ）‎ A. 四边形内角和等于外角和 B. 相似多边形的面积比等于相似比 C. 点P（1,2）关于原点对称的点的坐标为（-1，-2）‎ D. 三角形的中位线平行于第三边，且等于第三边的一半 6. 如果 （ C ）‎ A.3和-2 B.-3和2 C.3和2 D.-3和-2‎ 7. 如图2，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为 （ A ）‎ A.30° B.40°‎ C.50° D.60°‎ 二、 填空题（本大题共8个小题，每小题3分，满分24分）‎ ‎8．的相反数是 ‎9. 四次 测试小丽每分钟做仰卧起坐的次数分别为：50、45、48、47，这组数据的中位数为___47.5____.‎ ‎10. 红河州初中毕业生参加今年中考的学生数约是36600人，这个数用科学记数法可表示为3.66×104 ‎ ‎11. 如图3，D、E分别是AB、AC上的点，若∠A=70°，∠B=60°，‎ ‎ DE//BC.则∠AED的度数是 50°.‎ ‎12. 已知一次函数y=-3x+2，它的图像不经过第 三 象限.‎ ‎13. 计算：+2sin60°= ‎ ‎14. 已知圆锥的底面直径为4，母线长为6，则它的侧面展开图的圆心角为 120° .‎ ‎…‎ 图4‎ ‎15. 如图4，在图（1）中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，在图（2）中，A2、B2、C2分别是△A1B1C1的边B1C1、C1 A1、 A1B1的中点，…，按此规律，则第n个图形中平行四边形的个数共有 3n 个.‎ 一、 解答题（本大题共8个小题，满分75分）‎ ‎16. （本小题满分7分）先化简再求值：选一个使原代数式有意义的数带入求值.‎ 解：原式=‎ ‎ =‎ ‎ =‎ ‎ =‎ ‎ 当 原式=‎ ‎17.（本小题满分9分）如图5，一架飞机在空中P处探测到某高山山顶D处的俯角为60°，‎ 此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行，飞行10秒到山顶D的正上方C处，此时测得飞机距地平面的垂直高度为12千米，求这座山的高（精确到0.1千米）‎ A B ‎12千米 P C D G ‎60°‎ 图5‎ 解：延长CD交AB于G，则CG=12（千米）‎ 依题意：PC=300×10=3000（米）=3（千米）‎ 在Rt△PCD中：‎ PC=3，∠P=60°‎ CD=PC·tan∠P ‎ =3×tan60°‎ ‎ =‎ ‎∴12-CD=12-≈6.8（千米）‎ 答：这座山的高约为6.8千米.‎ ‎18. (本小题满分9分)如图6，在正方形ABCD中，G是BC上的任意一点，（G与B、C两点不重合），E、F是AG上的两点（E、F与A、G两点不重合），若AF=BF+EF，∠1=∠2，请判断线段DE与BF有怎样的位置关系，并证明你的结论.‎ 解：根据题目条件可判断DE//BF.‎ 证明如下：‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB=AD，∠BAF+∠2=90°.‎ ‎∵AF=AE+EF，又AF=BF+EF ‎∴AE=BF ‎∵∠1=∠2，∴△ABF≌△DAE（SAS）.‎ ‎∴∠AFB=∠DEA，∠BAF=∠ADE.‎ ‎∴∠ADE+∠2=90°，‎ ‎∴∠AED=∠BFA=90°.‎ ‎∴DE//BF. ‎ ‎19. (本小题满分8分)某中学计划对本校七年级10个班的480名学生按“学科”、“文体”、“手工”三个项目安排课外兴起小组，小组小明从每个班中随机抽取5名学生进行问卷调查，并将统计结果制成如下所示的表和图7.‎ ‎（1）请将统计表、统计图补充完整；‎ ‎（2）请以小明的统计结果来估计该校七年级480名学生参加各个项目的人数.‎ 兴起小组 划 记 频数 百分比 学科 正正正正正 ‎25‎ 文体 正正 手工 正正正 合计 ‎50‎ ‎50‎ 解：‎ 兴起小组 划 记 频数 百分比 学科 正正正正正 ‎25‎ ‎50%‎ 文体 正正 ‎10‎ ‎20%‎ 手工 正正正 ‎15‎ ‎30%‎ 合计 ‎50‎ ‎50‎ ‎100%‎ （1） 统计表、统计图补充如上；‎ （2） 七年级480名学生参加个项目人数约为：‎ 学科：480×50%=240（人）‎ 文体：480×20%=96（人）‎ 手工：480×30%=144（人）‎ 答：该校七年级480名学生参加“学科”、“文体”、“手工”三个项目的人数分别约为240人，96人，144人.‎ ‎20. （本小题满分8分）现有一本故事书，姐妹俩商定通过摸球游戏定输赢（赢的一方先看），游戏规则是：用4个完全相同的小球，分别表上1、2、3、4后放进一个布袋内，先由姐姐从布袋中任意摸出一个小球，记下小球的标号后放回并摇匀，再由妹妹任意摸出一个小球，若两人摸出的小球标号之积为偶数，则姐姐赢，两人摸出的小球标号之积为奇数，则妹妹赢.这个游戏规则对双方公平吗？请利用树状图或列表法说明理由.‎ 解：树状图如下图：‎ 或列表如下表：‎ 妹妹 姐姐 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎1×1=1‎ ‎1×2=2‎ ‎1×3=3‎ ‎1×4=4‎ ‎2‎ ‎2×1=2‎ ‎2×2=4‎ ‎2×3=6‎ ‎2×4=8‎ ‎3‎ ‎3×1=3‎ ‎3×2=6‎ ‎3×3=9‎ ‎3×4=12‎ ‎4‎ ‎4×1=4‎ ‎4×2=8‎ ‎4×3=12‎ ‎4×4=16‎ 由上述树状图或表格知：所有可能出现的结果共有16种.‎ ‎∴ P（姐姐赢）= P（妹妹赢）=‎ 所以此游戏对双方不公平，姐姐赢的可能性大.‎ ‎21.（本小题满分9分）师徒二人分别组装28辆摩托车，徒弟单独工作一周（7天）不能完成，而师傅单独工作不到一周就已完成，已知师傅平均每天比徒弟多组装2辆，求：‎ ‎（1）徒弟平均每天组装多少辆摩托车（答案取整数）？‎ ‎（2）若徒弟先工作2天，师傅才开始工作，师傅工作几天，师徒两人做组装的摩托车辆数相同？‎ 解：（1）设徒弟每天组装x辆摩托车，则师傅每天组装（x+2）辆.依题意得：‎ ‎7x<28‎ ‎7(x+2)>28‎ ‎ 解得2时，二次函数的函数值大于0.‎ ‎23.（本小题满分14分）如图9，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=cm，点B在y轴的正半轴上，OB=12cm，动点P从点O开始沿OA以cm/s的速度向点A移动，动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s.‎ ‎（1）求∠OAB的度数.‎ ‎（2）以OB为直径的⊙O‘与AB交于点M，当t为何值时，PM与⊙O‘相切？‎ ‎（3）写出△PQR的面积S随动点移动时间t的函数关系式，并求s的最小值及相应的t值.‎ ‎（4）是否存在△APQ为等腰三角形，若存在，求出相应的t值，若不存在请说明理由.‎ 解：（1）在Rt△AOB中：‎ tan∠OAB=‎ ‎∴∠OAB=30°‎ ‎（2）如图10，连接O‘P，O‘M. 当PM与⊙O‘相切时，有∠PM O‘=∠PO O‘=90°，‎ ‎ △PM O‘≌△PO O‘‎ 由（1）知∠OBA=60°‎ ‎∵O‘M= O‘B ‎∴△O‘BM是等边三角形 ‎∴∠B O‘M=60°‎ 可得∠O O‘P=∠M O‘P=60°‎ ‎∴OP= O O‘·tan∠O O‘P ‎ =6×tan60°=‎ 又∵OP=t ‎∴t=，t=3‎ 即：t=3时，PM与⊙O‘相切.‎ ‎（3）如图9，过点Q作QE⊥x于点E ‎ ∵∠BAO=30°，AQ=4t ‎ ∴QE=AQ=2t ‎ AE=AQ·cos∠OAB=4t×‎ ‎∴OE=OA-AE=-t ‎ ∴Q点的坐标为（-t，2t）‎ ‎ S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ ‎ =‎ ‎ =‎ ‎ = （）‎ ‎ 当t=3时，S△PQR最小=‎ ‎ （4）分三种情况：如图11.‎ 当AP=AQ1=4t时，‎ ‎∵OP+AP=‎ ‎∴t+4t=‎ ‎∴t=‎ 或化简为t=-18‎ 当PQ2=AQ2=4t时 ‎ 过Q2点作Q2D⊥x轴于点D，‎ ‎∴PA=2AD=2A Q2·cosA=t 即t+t =‎ ‎∴t=2‎ 当PA=PQ3时，过点P作PH⊥AB于点H ‎ AH=PA·cos30°=（-t）·=18-3t AQ3=2AH=36-6t 得36-6t=4t，‎ ‎∴t=3.6‎ ‎ 综上所述，当t=2，t=3.6，t=-18时，△APQ是等腰三角形.‎