- 2021-11-11 发布 |
- 37.5 KB |
- 6页


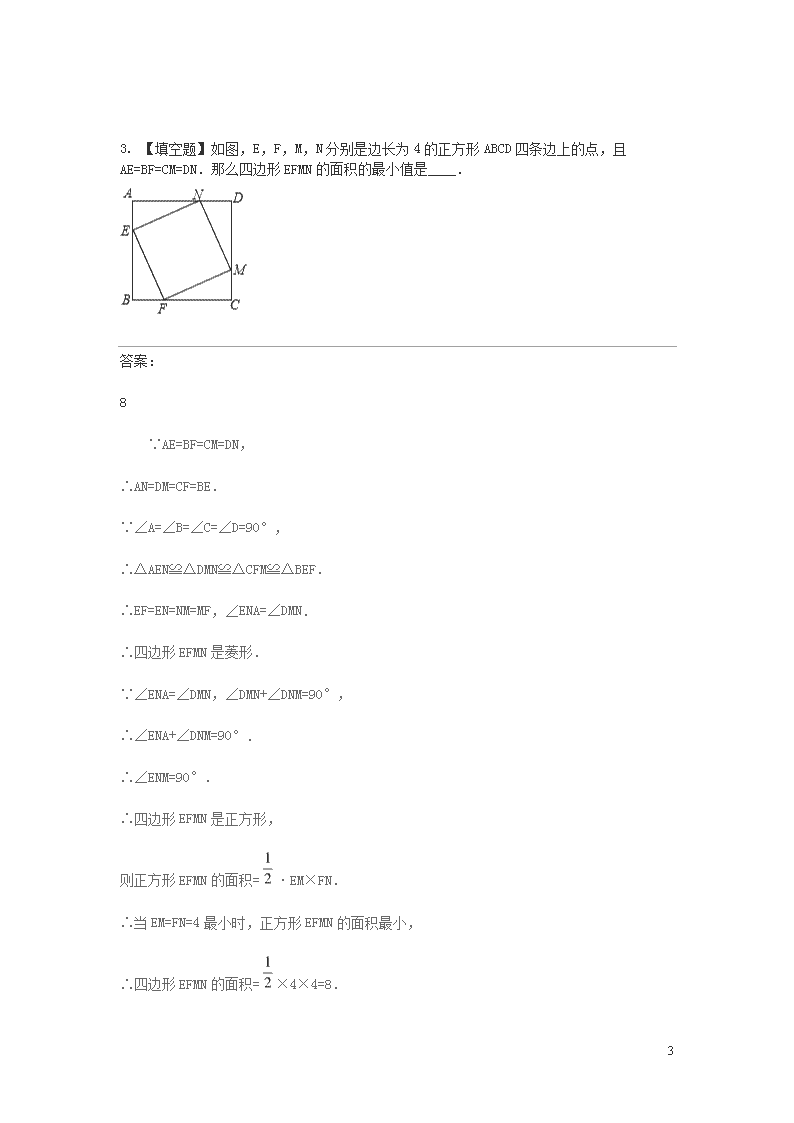
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学下学期期末考前练习题填空题提高
填空题(提高) 1. 【填空题】如图,直线上有三个正方形a,b,c,若a,c的面积分别为5和12,则b的面积为____. 答案: 17 解析 由于a、b、c都是正方形,所以AC=CD,∠ACD=90°, ∵∠ACB+∠DCE=∠ACB+∠BAC=90°,即∠BAC=∠DCE, ∠ABC=∠CED=90°,AC=CD, ∴△ACB≌△DCE, ∴AB=CE,BC=DE, 在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2, 即Sb=Sa+Sc=12+5=17. 故答案为:17. 2. 【填空题】边长为a的菱形是由边长为a的正方形“形变”得到的,若这个菱形一组对边之间的距离为h,则称为这个菱形的“形变度”. 1小题1.一个“形变度”为2的菱形与其“形变”前的正方形的面积之比为____. 6 答案: 1:2 2小题2.如图,A、B、C为菱形网格(每个小菱形的边长为1,“形变度”为)中的格点,则△ABC的面积为____. 答案: 解析(1)∵边长为a的正方形面积=a2,边长为a的菱形面积=ah, ∴菱形面积:正方形面积=ah:a2=h:a, ∵菱形的变形度为2,即, ∴“形变度”为2的菱形与其“形变”前的正方形的面积之比=1:2. 故答案为:1:2. (2)∵菱形的边长为1,“形变度”为, ∴菱形形变前的面积与形变后的面积之比为, ∴S△ABC=. 故答案为:. 6 3. 【填空题】如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是____. 答案: 8 解析∵AE=BF=CM=DN, ∴AN=DM=CF=BE. ∵∠A=∠B=∠C=∠D=90°, ∴△AEN≌△DMN≌△CFM≌△BEF. ∴EF=EN=NM=MF,∠ENA=∠DMN. ∴四边形EFMN是菱形. ∵∠ENA=∠DMN,∠DMN+∠DNM=90°, ∴∠ENA+∠DNM=90°. ∴∠ENM=90°. ∴四边形EFMN是正方形, 则正方形EFMN的面积=·EM×FN. ∴当EM=FN=4最小时,正方形EFMN的面积最小, ∴四边形EFMN的面积=×4×4=8. 6 故答案为:8. 4. 【填空题】如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为____. 答案: 4 解析过点A作AE⊥BC于E,AF⊥CD于F,连接AC,BD相较于点O, ∵两条纸条宽度相同, ∴AE=AF. ∵AB∥CD,AD∥BC, ∴四边形ABCD是平行四边形. ∵S▱ABCD=BC·AE=CD·AF. 又∵AE=AF, ∴BC=CD, ∴四边形ABCD是菱形, 6 ∴AC⊥BD,AO=AC=1, ∴BO==2, ∴BD=2BO=4. 故答案为:4. 5. 【填空题】在实数范围内因式分解:x2y-3y=____. 答案: y(x-)(x+) 解析原式=y(x2-3)=y(x-)(x+). 故答案为:y(x-)(x+). 6. 【填空题】若最简二次根式与是同类二次根式,则a+b=____. 答案: 2 解析∵最简二次根式与是同类二次根式, ∴, 6 解得:, 则a+b=2. 故答案为:2. 6查看更多