2020九年级数学上册 第4章 相似三角形阶段性测试（十）练习 （新版）浙教版

2020九年级数学上册 第4章 相似三角形阶段性测试（十）练习 （新版）浙教版

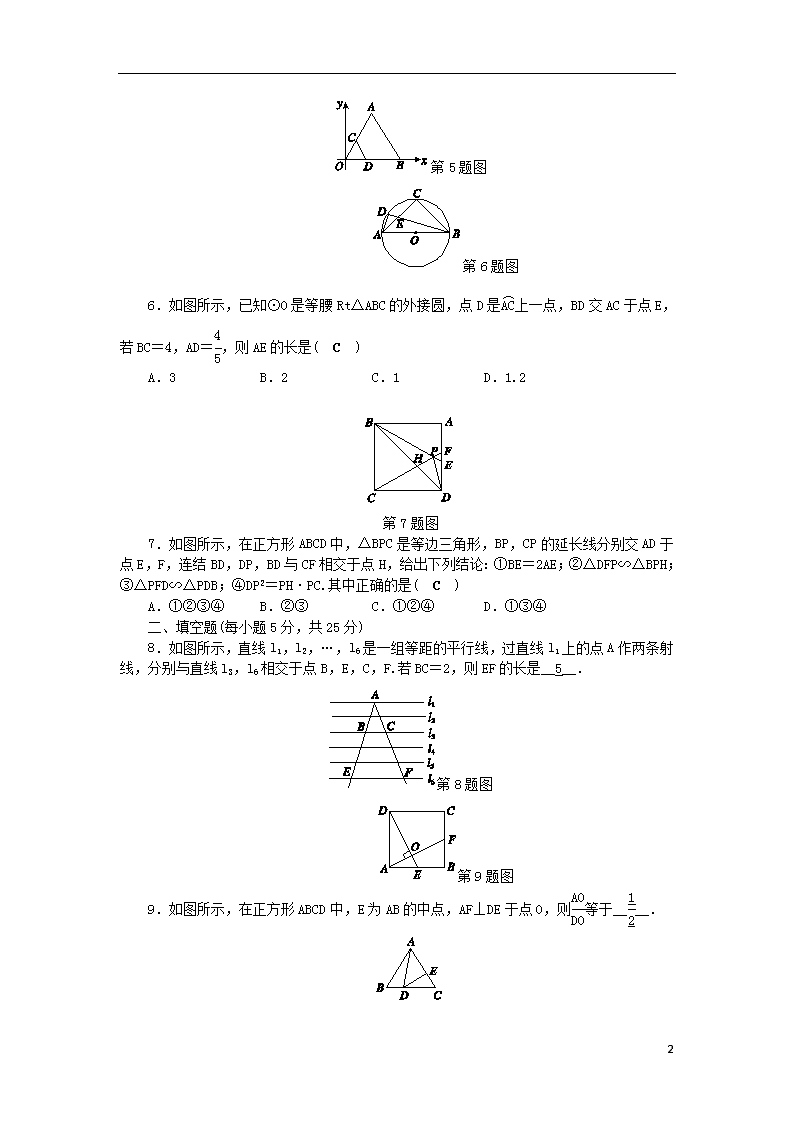
阶 段 性 测 试(十)‎ ‎(见学生单册)‎ ‎[考查范围：相似三角形(4.1～4.7)]‎ 一、选择题(每小题4分，共28分)‎ ‎1．两个相似三角形的面积比为1∶4，则它们的相似比为(　B　)‎ A．1∶4 B．1∶‎2 ‎ C．1∶16 D．无法确定 ‎2．如图所示，在△ABC中，点D在边AB上，BD＝2AD，DE∥BC交AC于点E，若线段DE＝5，则线段BC的长为(　C　)‎ A．7.5 B．‎10 ‎ C．15 D．20‎ 第2题图 ‎　　　　　第3题图 ‎3．如图所示，下列条件不能判定△ADB∽△ABC的是(　D　)‎ A．∠ABD＝∠ACB B．∠ADB＝∠ABC C．AB2＝AD·AC D.＝ ‎4．如图所示，已知点C，D都是线段AB的黄金分割点，如果CD＝4，则AB的长度是(　C　)‎ 第4题图 A．2 B．6－‎2‎ C．8＋4 D．2＋ ‎5．如图所示，线段CD两个端点的坐标分别为C(1，2)，D(2，0)，以原点为位似中心，将线段CD放大得到线段AB，若点B的坐标为(5，0)，则点A的坐标为(　B　)‎ A．(2，5) B．(2.5，5) C．(3，5) D．(3，6)‎ 5‎ 第5题图 ‎　　　　　第6题图 ‎6．如图所示，已知⊙O是等腰Rt△ABC的外接圆，点D是上一点，BD交AC于点E，若BC＝4，AD＝，则AE的长是(　C　)‎ A．3 B．‎2 ‎ C．1 D．1.2‎ 第7题图 ‎7．如图所示，在正方形ABCD中，△BPC是等边三角形，BP，CP的延长线分别交AD于点E，F，连结BD，DP，BD与CF相交于点H，给出下列结论：①BE＝2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2＝PH·PC.其中正确的是(　C　)‎ A．①②③④ B．②③ C．①②④ D．①③④‎ 二、填空题(每小题5分，共25分)‎ ‎8．如图所示，直线l1，l2，…，l6是一组等距的平行线，过直线l1上的点A作两条射线，分别与直线l3，l6相交于点B，E，C，F.若BC＝2，则EF的长是__5__．‎ 第8题图 ‎　　　　　第9题图 ‎9．如图所示，在正方形ABCD中，E为AB的中点，AF⊥DE于点O，则等于____．‎ 5‎ 第10题图 ‎10．如图所示，在边长为9的正三角形ABC中，D，E分别是BC，AC上的一点，BD＝3，已知∠ADE＝60°，则AE的长为__7__．‎ ‎11．在平行四边形ABCD中，点E在直线AD上，AE＝AD，连结CE交BD于点F，则EF∶FC的值是__或__．‎ 第12题图 ‎12．如图所示，在△ABC中，AB＝AC＝a，BC＝b(a＞b)．在△ABC内依次作∠CBD＝∠A，∠DCE＝∠CBD，∠EDF＝∠DCE.则EF等于____．‎ 三、解答题(5个小题，共47分)‎ ‎13．(8分)在13×13的网格图中，已知△ABC和点M(1，2)．‎ ‎(1)以点M为位似中心，画出△ABC的位似图形△A′B′C′，使△ABC和△A′B′C′的位似比为2；‎ ‎(2)写出△A′B′C′的各顶点坐标．‎ 第13题图 解：(1)如图所示：‎ 第13题答图 ‎(2)△A′B′C′的各顶点坐标分别为A′(3，6)，B′(5，2)，C′(11，4)．‎ 5‎ 第14题图 ‎14．(9分)如图所示，M，N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞．工程人员为计算工程量，必须测量M，N两点之间的直线距离．选择测量点A，B，C，点B，C分别在AM，AN上，现测得AM＝‎1千米，AN＝1.8千米，AB＝‎54米，BC＝‎45米，AC＝‎30米．求M，N两点之间的直线距离．‎ 解：连结MN.∵＝＝，＝＝，∴＝.‎ 又∵∠BAC＝∠NAM，∴△BAC∽△MAN，∴＝，‎ ‎∴MN＝＝1500(米)．‎ 即M，N两点之间的直线距离为1500米．‎ 第15题图 ‎15．(10分)如图所示，∠ACB＝90°，AC＝BC，AD⊥CE于点D，BE⊥CE于点E.‎ ‎(1)求证：△ACD≌△CBE；‎ ‎(2)已知AD＝4，DE＝1，求EF的长. ‎ 解：(1)证明：∵AD⊥CE，∴∠2＋∠3＝90°.‎ 又∵∠1＋∠2＝90°，∴∠1＝∠3.‎ 又∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°.‎ 在△ACD和△CBE中， ‎∴△ACD≌△CBE.‎ ‎(2)∵△ACD≌△CBE，∴CE＝AD＝4.∴CD＝CE－DE＝3.‎ ‎∵∠E＝∠ADF，∠BFE＝∠AFD，∴△BEF∽△ADF.∴＝.‎ 设EF＝x，则DF＝1－x，∴＝，解得x＝，即EF＝.‎ 第16题图 5‎ ‎16．(10分)如图所示，在△ABC中，AB＝AC，点P，D分别是BC，AC边上的点，∠APD＝∠B.‎ ‎(1)求证：AC·CD＝CP·BP.‎ ‎(2)若AB＝10，BC＝12，当PD∥AB时，求BP的长．‎ 解：(1)证明：∵AB＝AC，∴∠B＝∠C.∵∠APD＝∠B，‎ ‎∴∠APD＝∠B＝∠C.‎ ‎∵∠APC＝∠BAP＋∠B，∠APC＝∠APD＋∠DPC，‎ ‎∴∠BAP＝∠DPC，∴△ABP∽△PCD，∴＝，‎ ‎∴AB·CD＝CP·BP.∵AB＝AC，∴AC·CD＝CP·BP.‎ ‎(2)∵PD∥AB，∴∠APD＝∠BAP.由(1)可知∠APD＝∠C，‎ ‎∴∠BAP＝∠C.∵∠B＝∠B，∴△BAP∽△BCA，∴＝.‎ ‎∵AB＝10，BC＝12，∴＝，∴BP＝.‎ 第17题图 ‎17．(10分)在锐角△ABC中，边BC长为18，高AD长为12.‎ ‎(1)如图，矩形EFCH的边GH在BC边上，其余两个顶点E，F分别在AB，AC边上，EF交AD于点K，求的值；‎ ‎(2)设EH＝x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值．‎ 解：(1)∵△AEF∽△ABC，∴＝，‎ ‎∵边BC长为18，高AD长为12，‎ ‎∴＝＝.‎ ‎(2)∵EH＝KD＝x，‎ ‎∴AK＝12－x，EF＝(12－x)，‎ ‎∴S＝(12－x)x＝－(x－6)2＋54，‎ 当x＝6时，S有最大值为54.‎ 5‎