- 2021-11-11 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学中考总复习课件PPT:第6课时 一次方程(组)及其应用
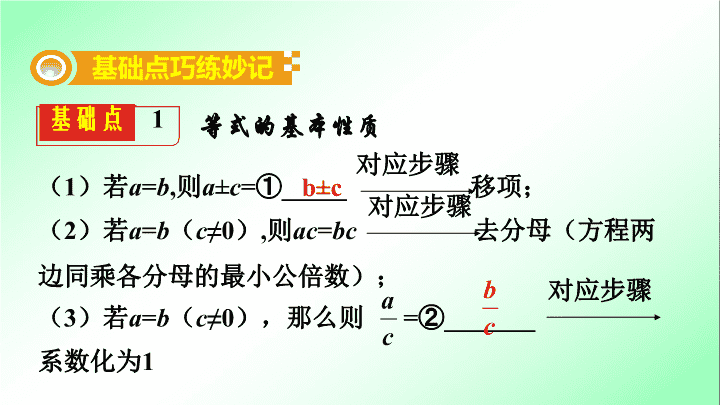
第一部分 夯实基础 提分多 第 二 单元 方程(组)与不等式(组) 第 6 课时 一次方程(组)及其应用 基础点 1 等式的基本性质 基础点巧练妙记 (1)若 a = b ,则 a ± c =① _ ____ 移项; (2)若 a = b ( c ≠0),则 ac = bc 去分母(方程两边同乘各分母的最小公倍数); (3)若 a = b ( c ≠0),那么则 =② _ ______ 系数化为 1 b±c 对应步骤 对应步骤 对应步骤 1. 定义 :只含有③ _ _____ 未知数(元),未知数的次数都是④ _ ___ (系数不为0),等号两边都是整式的方程. 2. 一元一次方程的解法 基础点 2 一元一次方程及其解法 一个 1 1. 解一元一次方程: (1) x -3= x + 2 ; 练 提 分 必 x =-10 (2) 4 x +3 ( x -2 ) = 7- ( 2 x +4 ); x =1 (3) -2=3+ . x =4 练 提 分 必 【 温馨提示 】 ( 1 )去括号时,要注意括号前系数的正负;若系数为负,则去掉括号后每一项都要变号; ( 2 )去分数的分母时,要注意给等号左右两边的每一项都乘以该分母上的数字 . 基础点 3 二元一次方程(组)及其解法 1. 二元一次方程 :含有两个未知数(二元),并且含有未知数的项的次数都是 1 的整式方程 . 2. 二元一次方程组 :两个含有相同未知数的二元一次方程(或者一个二元一次方程,一个一元一次方程)联立起来组成的方程组 . 3. 解二元一次方程组的基本思想 二元一次方程组 一元一次方程 4. 二元一次方程组的解法 代入 消元 ( 1 ) 代入消元法 (适用于方程组中的其中一个方程的常数项为 0 或者某一个未知数的系数为 1 或 -1 时) a. 变 —— 用含有一个未知数的代数式表示另一个未知数; b. 代 —— 将所得代数式代入另一个方程消去一个元,化为一元一次方程 . ( 2 ) 加减消元法 a. 变 —— 将方程中的某个未知数的系数变为相同或互为相 反数 b. 加减 —— 消去一个元 如果是求代数式 ax±ay 的值,常用整体代入法求解 . 2.解二元一次方程组: (1) ( 2 ) 练 提 分 必 5. 三元一次方程组及其解法 三元一次方程组 二元一次方程组 一元一次方程 消元(代入或加减) 消元(代入或加减) 基础点 4 一次方程(组)的实际应用 常见应用题类型及等量关系 (1)利润问题: 售价=标价×折扣;销售额=售价×销量; 利润=售价-进价;利润率= ×100%. (2)分配问题:总量=甲的数量+乙的数量;总金额=甲的金额+乙的金额. 进价 利润 类型 一次方程(组)的实际应用 重难点精讲优练 例1 某种商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为 _ _____ 元;某商场在“双十一”这一天进行打折促销活动,若购物满288元,则超出部分一律按8折优惠.若小金购买商品刚好达到500元,则所需支付的费用为 _ ____ 元. 240 457.6 例2 食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A,B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A,B两种饮料共100瓶,问A,B两种饮料各生产了多少瓶? 解法一:设A种饮料生产了x瓶; 则 B 种饮料生产了 (100 - x ) 瓶,根据题意, 得 2 x + 3(100 - x ) = 270 ,解得 x = 30 , ∴ 100 - x = 100 - 30 = 70. 答: A 饮料生产了 30 瓶, B 饮料生产了 70 瓶. 解法二:设A种饮料生产了 x 瓶,B种饮料生产了 y 瓶. 根据题意列方程组, 解得 答: A 种饮料生产了 30 瓶, B 种饮料生产了 70 瓶. 练习 已知小明买了2瓶A种饮料和3瓶B种饮料共花费14元,小亮买了3瓶A种饮料和2瓶B种饮料共花费16元,求A、B两种饮料每瓶分别多少元? 解 : 设A种饮料每瓶 x 元,则B种饮料每瓶 y 元,根据 题意列方程组,得 ,解得 答:A种饮料每瓶4元,B种饮料每瓶2元.查看更多