呼和浩特专版2020中考数学复习方案第三单元函数及其图象第13课时二次函数的图象与性质课件

呼和浩特专版2020中考数学复习方案第三单元函数及其图象第13课时二次函数的图象与性质课件

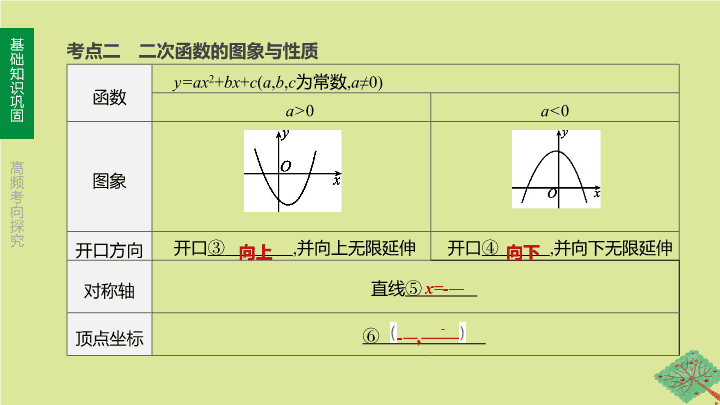
第 13 课时 二次函数的图象与性质 第三单元　函数及其图象 考点一　二次函数的概念 考点聚焦 一般地 , 形如 ① 　　　　　　 ( a , b , c 是常数 , a ≠0) 的函数 , 叫做二次函数 .  y=ax 2 + bx + c 【 温馨提示 】 函数 y=ax 2 + bx + c 未必是二次函数 , 当 ② 　　　　 时 , y=ax 2 + bx + c 是二次函数 . a ≠0 函数 　 y=ax 2 + bx + c ( a , b , c 为常数 , a ≠0) 　 a> 0 a< 0 图象 开口方向 　 开口 ③ 　　　　 , 并向上无限延伸   　 开口 ④ 　　　 , 并向下无限延伸   对称轴 　 直线 ⑤ 　　　   顶点坐标 　 ⑥ 　　　　　　   考点二　二次函数的图象与性质 向上 向下 （续表） 减小 增大 增大 减小 （续表） 小 大 考点三　二次函数 y = ax 2 + bx + c ( a , b , c 为常数 , a ≠0) 的图象与系数的关系 上 下 y 左 右 ( 续表 ) (0,0) 正半轴 负半轴 两 ( 续表 ) a - b + c -1 考点四　二次函数图象的画法 考点五　二次函数的表示及解析式的求法 1 . 二次函数的三种表示方法 (1) 一般式 : ㉔ 　　　　　　　　　　 .  (2) 顶点式 : y=a ( x - h ) 2 + k ( a ≠0), 其中二次函数图象的顶点坐标是 ㉕ 　　　　 .  (3) 两点式 : y=a ( x - x 1 )( x - x 2 )( a ≠0), 其图象与 x 轴的交点的坐标为 ㉖ 　　　　 .  y=ax 2 + bx + c ( a ≠0) ( h , k ) ( x 1 ,0),( x 2 ,0) 2 . 二次函数解析式的确定 用待定系数法求二次函数的解析式时 , 注意解析式的设法 , 常见情况如下 : 条件 设法 顶点在原点 y=ax 2 ( a ≠0) 顶点在 y 轴上 　 y=ax 2 + c ( a ≠0, y 轴为对称轴 ) 顶点在 x 轴上 　 y=a ( x - h ) 2 ( a ≠0, 直线 x=h 是对称轴 ) 抛物线过原点 y=ax 2 + bx ( a ≠0) 顶点 ( h , k ) y=a ( x - h ) 2 + k ( a ≠0) 抛物线与 x 轴的 交点 为 ( x 1 ,0),( x 2 ,0) y=a ( x - x 1 )( x - x 2 )( a ≠0) 考点六　二次函数图象的平移 抛物线 y=ax 2 + bx + c ( a ≠0) 可用配方法化成 y=a ( x - h ) 2 + k ( a ≠0) 的形式 , 任意抛物线 y=a ( x - h ) 2 + k ( a ≠0) 均可由抛物线 y=ax 2 ( a ≠0) 平移得到 , 具体平移方法如图 13-1 所示 ( 假设 h , k 均为正数 ): 图 13-1 【 温馨提示 】 平移规则为 “ 上加下减 , 左加右减 ” . 题组一　必会题 对点演练 1 . [2018· 岳阳 ] 抛物线 y= 3( x -2) 2 +5 的顶点坐标是 ( 　　 ) A . (-2,5) B . (-2,-5) C . (2,5) D . (2,-5) C 2 . [2019· 重庆 B 卷 ] 抛物线 y= -3 x 2 +6 x +2 的对称轴是 ( 　　 ) A . 直线 x= 2 B . 直线 x= -2 C . 直线 x= 1 D . 直线 x= -1 C 3 . 一条抛物线和抛物线 y= -2 x 2 的形状、开口方向完全相同 , 顶点坐标是 (-1,3), 则该抛物线的解析式为 ( 　　 ) A .y= -2( x -1) 2 +3 B .y= -2( x +1) 2 +3 C .y= -(2 x +1) 2 +3 D .y= -(2 x -1) 2 +3 B 4 . [2019· 雅安 ] 在平面直角坐标系中 , 对于二次函数 y= ( x -2) 2 +1, 下列说法中错误的是 ( 　　 ) A .y 的最小值为 1 B . 图象顶点坐标为 (2,1), 对称轴为直线 x= 2 C . 当 x< 2 时 , y 的值随 x 值的增大而增大 , 当 x ≥2 时 , y 的值随 x 值的增大而减小 D . 它的图象可以由 y=x 2 的图象向右平移 2 个单位长度 , 再向上平移 1 个单位长度得到 C 5 . [2019· 河南 ] 已知抛物线 y= - x 2 + bx +4 经过 (-2, n ) 和 (4, n ) 两点 , 则 n 的值为 ( 　　 ) A . -2 B . -4 C . 2 D . 4 [ 答案 ]B 6 . [2019· 攀枝花 ] 在同一坐标系中 , 二次函数 y=ax 2 + bx 与一次函数 y=bx - a 的图象可能是 ( 　　 ) C 图 13-2 题组二　易错题 【 失分点 】 考虑二次函数的增减性时 , 要关注自变量的取值及对称轴的位置 , 因为二次函数的增减性是分区域的 . 7 . [2019· 温州 ] 已知二次函数 y=x 2 -4 x +2, 关于该函数在 -1≤ x ≤3 的取值范围内 , 下列说法正确的是 ( 　　 ) A . 有最大值 -1, 有最小值 -2 B . 有最大值 0, 有最小值 -1 C . 有最大值 7, 有最小值 -1 D . 有最大值 7, 有最小值 -2 [ 答案 ]D 　 [ 解析 ] ∵二次函数 y=x 2 -4 x +2 = ( x -2) 2 -2, ∴该函数在 -1≤ x ≤3 的取值范围内 , 当 x= 2 时 , y 有最小值 -2; 当 x= -1 时 , y 有最大值 7 . 故选 D . 8 . [2018· 潍坊 ] 已知二次函数 y= -( x - h ) 2 ( h 为常数 ), 当自变量 x 的值满足 2≤ x ≤5 时 , 与其对应的函数值 y 的最大值为 -1, 则 h 的值为 ( 　　 ) A . 3 或 6 B . 1 或 6 C . 1 或 3 D . 4 或 6 [ 答案 ]B 　 [ 解析 ] 二次函数 y= -( x - h ) 2 , 当 x=h 时 , 有最大值 0, 而当自变量 x 的值满足 2≤ x ≤5 时 , 与其对应的函数值 y 的最大值为 -1, 故 h< 2 或 h> 5 . 当 h< 2 时 ,2≤ x ≤5 时 , y 随 x 的增大而减小 , 故当 x= 2 时 , y 有最大值 , 此时 -(2- h ) 2 = -1, 解得 : h 1 = 1, h 2 = 3( 舍去 ), 此时 h= 1; 当 h> 5 时 ,2≤ x ≤5 时 , y 随 x 的增大而增大 , 故当 x= 5 时 , y 有最大值 , 此时 -(5- h ) 2 = -1, 解得 : h 1 = 6, h 2 = 4( 舍去 ), 此时 h= 6 . 综上可知 , h= 1 或 6, 故选 B . 9 . 一元二次方程 x 2 +( m -5) x +1- m= 0 的一根大于 3, 另一根小于 3, 则 m 的取值范围 为 　　　　 .  考向一　二次函数的图象与性质 图 13-3 解 :(1) y=x 2 -2 x -8 = ( x -1) 2 -9, 开口向上 , 对称轴为直线 x= 1, 顶点为 D (1,-9) . 例 1 对于抛物线 y=x 2 -2 x -8 . (2) 求出它与 y 轴的交点 C 的坐标 ; 图 13-3 (2) 令 x= 0, 则 y= -8, ∴ C (0,-8) . 例 1 对于抛物线 y=x 2 -2 x -8 . (3) 求出它与 x 轴的交点 A , B 的坐标 ( A 在 B 左侧 ); 图 13-3 (3) 令 y= 0, 则 x 2 -2 x -8 = 0, ∴ x 1 = -2, x 2 = 4, ∴ A (-2,0), B (4,0) . 例 1 对于抛物线 y=x 2 -2 x -8 . (4) 画出它的图象 ; 图 13-3 (4) 如图 : 例 1 对于抛物线 y=x 2 -2 x -8 . (5) 当 x 为何值时 , y 随 x 的增大而增大 ; 图 13-3 (5) 当 x ≥1 时 , y 随 x 的增大而增大 . 例 1 对于抛物线 y=x 2 -2 x -8 . (6) 求 CB 和 AD 的长 ; 图 13-3 例 1 对于抛物线 y=x 2 -2 x -8 . (7) 求 △ CDB 的面积 . 图 13-3 | 考向精练 | 1 . [2019· 呼和浩特 3 题 ] 二次函数 y=ax 2 与一次函数 y=ax + a 在同一坐标系中的大致图象可能是 ( 　　 ) D 图 13-4 2 . [2013· 呼和浩特 8 题 ] 在同一平面直角坐标系中 , 函数 y=mx + m 和 y= - mx 2 +2 x +2( m 是常数 , m ≠0) 的图象可能是 ( 　　 ) 图 13-5 D 3 . [2019· 烟台 ] 已知二次函数 y=ax 2 + bx + c 的 y 与 x 的部分对应值如下表 : 下列结论 : ①抛物线的开口向上 ; ②抛物线的对称轴为直线 x= 2; ③当 0 0; ④抛物线与 x 轴的两个交点间的距离是 4; ⑤若 A ( x 1 ,2), B ( x 2 ,3) 是抛物线上两点 , 则 x 1 x 2 , 所以结论⑤错误 . 4 . 当 a ≤ x ≤ a +1 时 , 函数 y=x 2 -2 x +1 的最小值为 1, 则 a 的值为 ( 　　 ) A . -1 B . 2 C . 0 或 2 D . -1 或 2 [ 答案 ] D 　 [ 解析 ] y=x 2 -2 x +1 = ( x -1) 2 , 该函数在实数范围内最小值为 0, 但题中说当 a ≤ x ≤ a +1 时 , 函数 y=x 2 -2 x +1 的最小值为 1, 因此 , 当 x=a 或 x=a +1 时 , 函数值为 1, 令 y= 1, 可得 x 1 = 0, x 2 = 2, 再由该函数的增减性可知 a +1 = 0, 或 a= 2, 即 a= -1 或 2, 故选 D . 5 . 已知二次函数 y= -( x -1) 2 +2, 当 t 1 时 , y 随 x 的增大而减小 , 而 t 0; ③ a - b + c< 0; ④ m> -2 . 其中正确结论的个数是 ( 　　 ) A . 1 B . 2 C . 3 D . 4 图 13-6 [ 答案 ] B 　 [ 解析 ] 直接利用抛物线与 x 轴交点个数以及抛物线与方程之间的关系、函数图象与各系数之间的关系分析 . 图象与 x 轴有两个交点 , 则 b 2 -4 ac> 0, 故①错误 ; ∵图象开口向上 , ∴ a> 0, ∵对称轴在 y 轴右侧 , ∴ a , b 异号 , ∴ b< 0, ∵图象与 y 轴交于负半轴 , ∴ c< 0, ∴ abc> 0, 故②正确 ; 当 x= -1 时 , a - b + c> 0, 故③错误 ; 抛物线 y=ax 2 + bx + c 顶点坐标的纵坐标为 -2, ∵关于 x 的一元二次方程 ax 2 + bx + c - m= 0 有两个不相等的实数根 , ∴ m> -2, 故④正确 . 故选 B . 【 方法点析 】 解此类问题的一般步骤 : ①根据抛物线的开口方向判定 a 的符号 : 开口向上 , 则 a> 0; 开口向下 , 则 a< 0 . ②根据对称轴的位置和 a 的符号判定 b 的符号 : 对称轴在 y 轴左侧 , 则 a , b 同号 ; 对称轴在 y 轴右侧 , 则 a , b 异号 . ③由抛物线与 y 轴的交点判断 c 的符号 : 交点在 y 轴正半轴 , 则 c> 0; 交点在 y 轴负半轴 , 则 c< 0 . ④根据 a , b , c 的符号判定 ab , bc , ac , abc 的符号 . ⑤根据抛物线与 x 轴的交点个数判定 b 2 -4 ac 与 0 的大小关系 . ⑥特殊等式的判断 : 见到 a + b + c ( 或 4 a +2 b + c ), 则令 x= 1( 或 x= 2), 看抛物线上对应点的纵坐标位置 ; 见到 a - b + c ( 或 4 a -2 b + c ), 则令 x= -1( 或 x= -2), 看抛物线上对应点的纵坐标的位置 , 根据位置判定其符号 . | 考向精练 | 1 . [2019· 玉泉区模拟 ] 已知二次函数 y=ax 2 + bx + c ( a ≠0) 的图象如图 13-7 所示 , 有下列 4 个结论 : ① a< 0; ② b> 0; ③ b 4 ac ; ③ a + b +2 c< 0; ④ 3 a + c> 0 . 其中正确的是 ( 　　 ) A . ①④ B . ②④ C . ①②③ D . ①②③④ 图 13-8 [ 答案 ] D 3 . [2019· 赤峰 ] 二次函数 y=ax 2 + bx + c ( a ≠0) 的图象如图 13-9 所示 , 下列结论 : ① b> 0; ② a - b + c= 0; ③一元二次方程 ax 2 + bx + c +1 = 0( a ≠0) 有两个不相等的实数根 ; ④当 x< -1 或 x> 3 时 , y> 0 . 上述结论中正确的是 　　　　 . ( 填上所有正确结论的序号 )  图 13-9 [ 答案 ] ②③④ [ 解析 ] 由图可知 , 对称轴为直线 x= 1, 与 x 轴的一个交点为 (3,0), ∴ b= -2 a , 与 x 轴另一个交点的坐标为 (-1,0), ①∵ a> 0, ∴ b< 0, ∴①错误 ; ②当 x= -1 时 , y= 0, ∴ a - b + c= 0, ②正确 ; ③一元二次方程 ax 2 + bx + c +1 = 0 的根可以看作抛物线 y=ax 2 + bx + c 与直线 y= -1 的交点的横坐标 , 由图象可知抛物线 y=ax 2 + bx + c 与直线 y= -1 有两个不同的交点 , ∴一元二次方程 ax 2 + bx + c +1 = 0( a ≠0) 有两个不相等的实数根 , ∴③正确 ; ④由图象可知 , 当 y> 0 时 , x< -1 或 x> 3, ∴④正确 . 故答案为②③④ . 考向三　二次函数图象的平移与旋转 例 3 [2019· 绍兴 ] 在平面直角坐标系中 , 抛物线 y= ( x +5)( x -3) 经过变换后得到抛物线 y= ( x +3)( x -5), 则这个变换可以是 ( 　　 ) A . 向左平移 2 个单位 B . 向右平移 2 个单位 C . 向左平移 8 个单位 D . 向右平移 8 个单位 [ 答案 ] B [ 解析 ] y= ( x +5)( x -3) = ( x +1) 2 -16, 顶点坐标是 (-1,-16) . y= ( x +3)( x -5) = ( x -1) 2 -16, 顶点坐标是 (1,-16) . 所以将抛物线 y= ( x +5)( x -3) 向右平移 2 个单位长度得到抛物线 y= ( x +3)( x -5), 故选 B . | 考向精练 | 1 . 将二次函数 y=x 2 -2 x +1 的图象绕它的顶点 A 旋转 180°, 则旋转后的抛物线所对应的函数解析式为 ( 　　 ) A .y= - x 2 +2 x +1 B .y= - x 2 -2 x +1 C .y= - x 2 +2 x -1 D .y=x 2 +2 x +1 C 2 . 在平面直角坐标系中 , 如果抛物线 y= 3 x 2 不动 , 而把 x 轴 , y 轴分别向上 , 向右平移 3 个单位 , 那么在新坐标系中抛物线的解析式为 　　 　　 .  y= 3( x +3) 2 -3 3 . 已知抛物线 y=a ( x - h ) 2 的对称轴为直线 x= -2, 且过点 (1,-3) . (1) 求抛物线的解析式 ; (2) 求将 (1) 中抛物线向右平移 3 个单位得到的抛物线的解析式 ; (3) 若 (2) 中抛物线的顶点不动 , 将抛物线沿 x 轴翻折 , 写出翻折后抛物线的解析式 . 考向四　二次函数解析式的确定 例 4 根据条件求解析式 . (1) 已知二次函数图象经过点 (2,-5),(-1,4),(-2,3), 求解析式 ; (2) 已知二次函数图象经过点 (-2,3), 且顶点为 (-1,4), 求解析式 ; (3) 已知二次函数图象经过点 (-3,0),(1,0),(0,3), 求解析式 ; (4) 已知二次函数图象经过点 (-2,3),(-1,4),(0,3), 求解析式 ; (5) 已知二次函数图象经过点 (-3,0),(-1,4),(1,0), 求解析式 . 例 4 根据条件求解析式 . (2) 已知二次函数图象经过点 (-2,3), 且顶点为 (-1,4), 求解析式 ; (2) ∵顶点为 (-1,4), ∴设解析式为 y=a ( x +1) 2 +4 . 将 (-2,3) 代入得 a= -1, ∴ y= -( x +1) 2 +4 . 例 4 根据条件求解析式 . (3) 已知二次函数图象经过点 (-3,0),(1,0),(0,3), 求解析式 ; (3) ∵二次函数图象与 x 轴交于 (-3,0),(1,0) 两点 , ∴设解析式为 y=a ( x +3)( x -1), 将 (0,3) 代入得 a= -1, ∴ y= -( x +3)( x -1), 即 y= - x 2 -2 x +3 . 例 4 根据条件求解析式 . (4) 已知二次函数图象经过点 (-2,3),(-1,4),(0,3), 求解析式 ; (4) 设对称点式为 y=a ( x +2)( x -0)+3, 将 (-1,4) 代入得 a= -1, ∴ y= -( x +2) x +3, 即 y= - x 2 -2 x +3 . 例 4 根据条件求解析式 . (5) 已知二次函数图象经过点 (-3,0),(-1,4),(1,0), 求解析式 . (5) 设交点式为 y=a ( x +3)( x -1), 将 (-1,4) 代入得 a= -1, ∴ y= - x 2 -2 x +3 . | 考向精练 | 2 . [2019· 泰州 ] 如图 13-10, 在平面直角坐标系 xOy 中 , 二次函数图象的顶点坐标为 (4,-3), 该图象与 x 轴相交于点 A , B , 与 y 轴相交于点 C , 其中点 A 的横坐标为 1 . (1) 求该二次函数的表达式 ; (2) 求 tan ∠ ABC. 图 13-10 2 . [2019· 泰州 ] 如图 13-10, 在平面直角坐标系 xOy 中 , 二次函数图象的顶点坐标为 (4,-3), 该图象与 x 轴相交于点 A , B , 与 y 轴相交于点 C , 其中点 A 的横坐标为 1 . (2) 求 tan ∠ ABC. 图 13-10