2020年秋九年级数学上册 第3章图形的相似

2020年秋九年级数学上册 第3章图形的相似

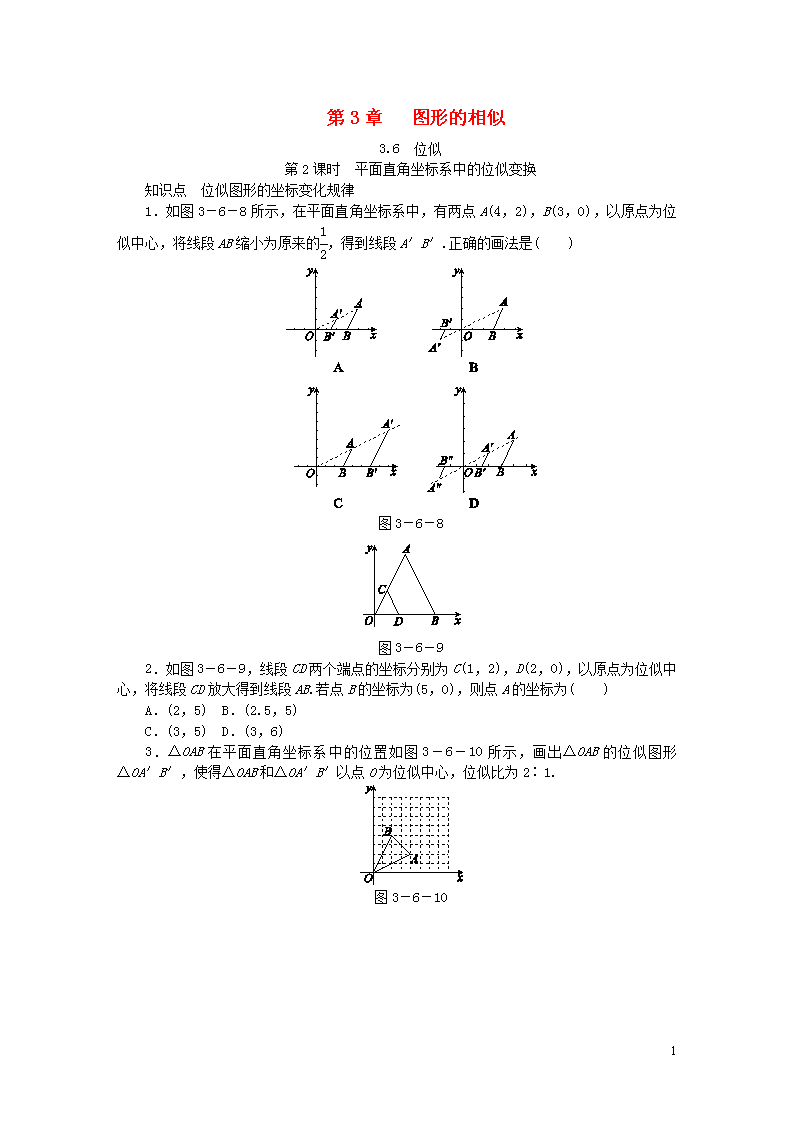
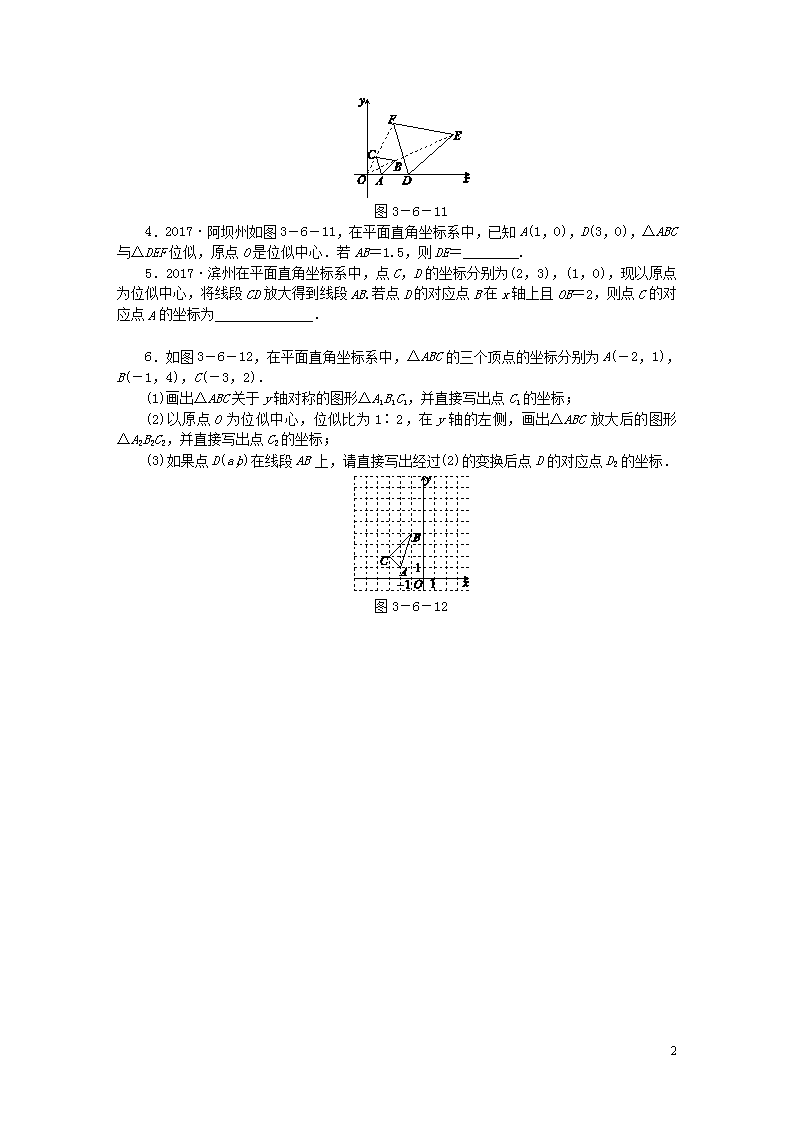
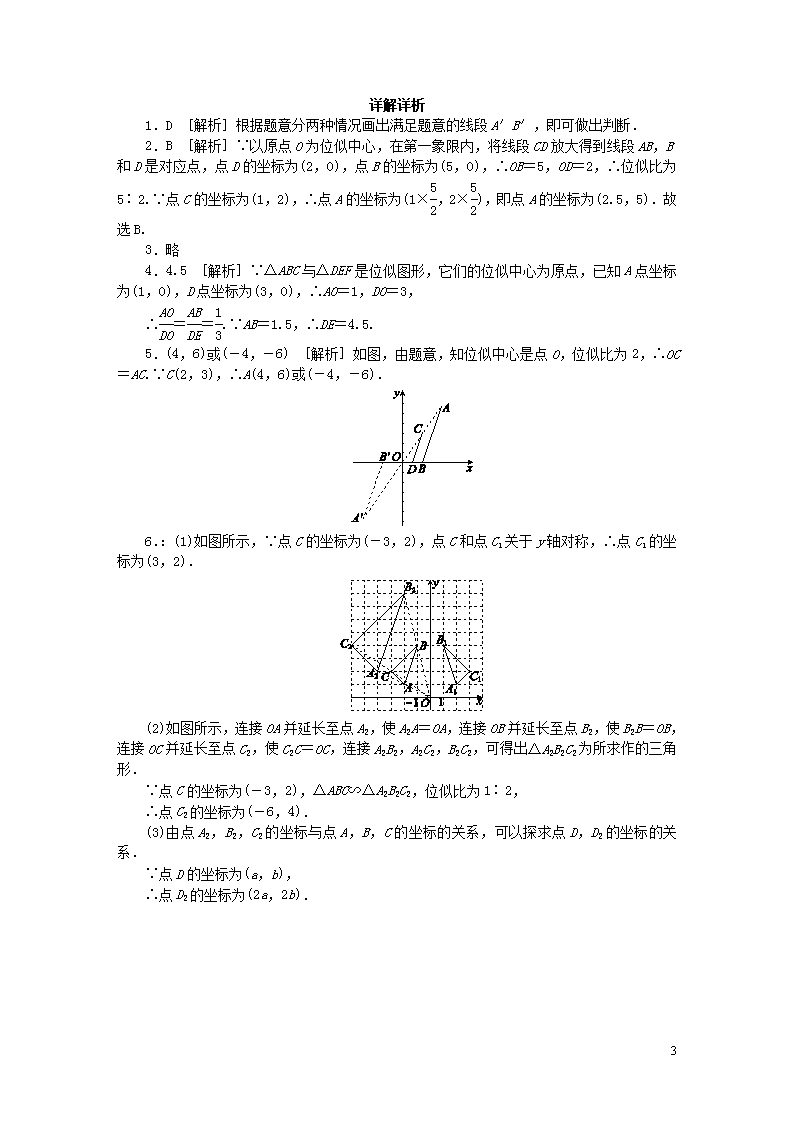
第3章 　图形的相似 ‎3.6　位似 第2课时 平面直角坐标系中的位似变换 知识点　位似图形的坐标变化规律 ‎1．如图3－6－8所示，在平面直角坐标系中，有两点A(4，2)，B(3，0)，以原点为位似中心，将线段AB缩小为原来的，得到线段A′B′.正确的画法是(　　)‎ 图3－6－8‎ 图3－6－9‎ ‎2．如图3－6－9，线段CD两个端点的坐标分别为C(1，2)，D(2，0)，以原点为位似中心，将线段CD放大得到线段AB.若点B的坐标为(5，0)，则点A的坐标为(　　)‎ A．(2，5) B．(2.5，5)‎ C．(3，5) D．(3，6)‎ ‎3．△OAB在平面直角坐标系中的位置如图3－6－10所示，画出△OAB的位似图形△OA′B′，使得△OAB和△OA′B′以点O为位似中心，位似比为2∶1.‎ 图3－6－10‎ 3‎ 图3－6－11‎ ‎4．2017·阿坝州如图3－6－11，在平面直角坐标系中，已知A(1，0)，D(3，0)，△ABC与△DEF位似，原点O是位似中心．若AB＝1.5，则DE＝________.‎ ‎5．2017·滨州在平面直角坐标系中，点C，D的坐标分别为(2，3)，(1，0)，现以原点为位似中心，将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB＝2，则点C的对应点A的坐标为______________．‎ ‎ ‎ ‎6．如图3－6－12，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(－2，1)，B(－1，4)，C(－3，2)．‎ ‎(1)画出△ABC关于y轴对称的图形△A1B‎1C1，并直接写出点C1的坐标；‎ ‎(2)以原点O为位似中心，位似比为1∶2，在y轴的左侧，画出△ABC放大后的图形△A2B‎2C2，并直接写出点C2的坐标；‎ ‎(3)如果点D(a，b)在线段AB上，请直接写出经过(2)的变换后点D的对应点D2的坐标．‎ 图3－6－12‎ ‎　　　　‎ 3‎ ‎详解详析 ‎1．D　[解析] 根据题意分两种情况画出满足题意的线段A′B′，即可做出判断．‎ ‎2．B　[解析] ∵以原点O为位似中心，在第一象限内，将线段CD放大得到线段AB，B和D是对应点，点D的坐标为(2，0)，点B的坐标为(5，0)，∴OB＝5，OD＝2，∴位似比为5∶2.∵点C的坐标为(1，2)，∴点A的坐标为(1×，2×)，即点A的坐标为(2.5，5)．故选B.‎ ‎3．略 ‎4．4.5　[解析] ∵△ABC与△DEF是位似图形，它们的位似中心为原点，已知A点坐标为(1，0)，D点坐标为(3，0)，∴AO＝1，DO＝3，‎ ‎∴＝＝.∵AB＝1.5，∴DE＝4.5.‎ ‎5．(4，6)或(－4，－6)　[解析] 如图，由题意，知位似中心是点O，位似比为2，∴OC＝AC.∵C(2，3)，∴A(4，6)或(－4，－6)．‎ ‎6．：(1)如图所示，∵点C的坐标为(－3，2)，点C和点C1关于y轴对称，∴点C1的坐标为(3，2)．‎ ‎(2)如图所示，连接OA并延长至点A2，使A‎2A＝OA，连接OB并延长至点B2，使B2B＝OB，连接OC并延长至点C2，使C‎2C＝OC，连接A2B2，A‎2C2，B‎2C2，可得出△A2B‎2C2为所求作的三角形．‎ ‎∵点C的坐标为(－3，2)，△ABC∽△A2B‎2C2，位似比为1∶2，‎ ‎∴点C2的坐标为(－6，4)．‎ ‎(3)由点A2，B2，C2的坐标与点A，B，C的坐标的关系，可以探求点D，D2的坐标的关系．‎ ‎∵点D的坐标为(a，b)，‎ ‎∴点D2的坐标为(‎2a，2b)．‎ 3‎