- 2021-11-11 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【精品试卷】中考数学一轮复习 专题测试14 反比例函数(培优提高)(教师版)
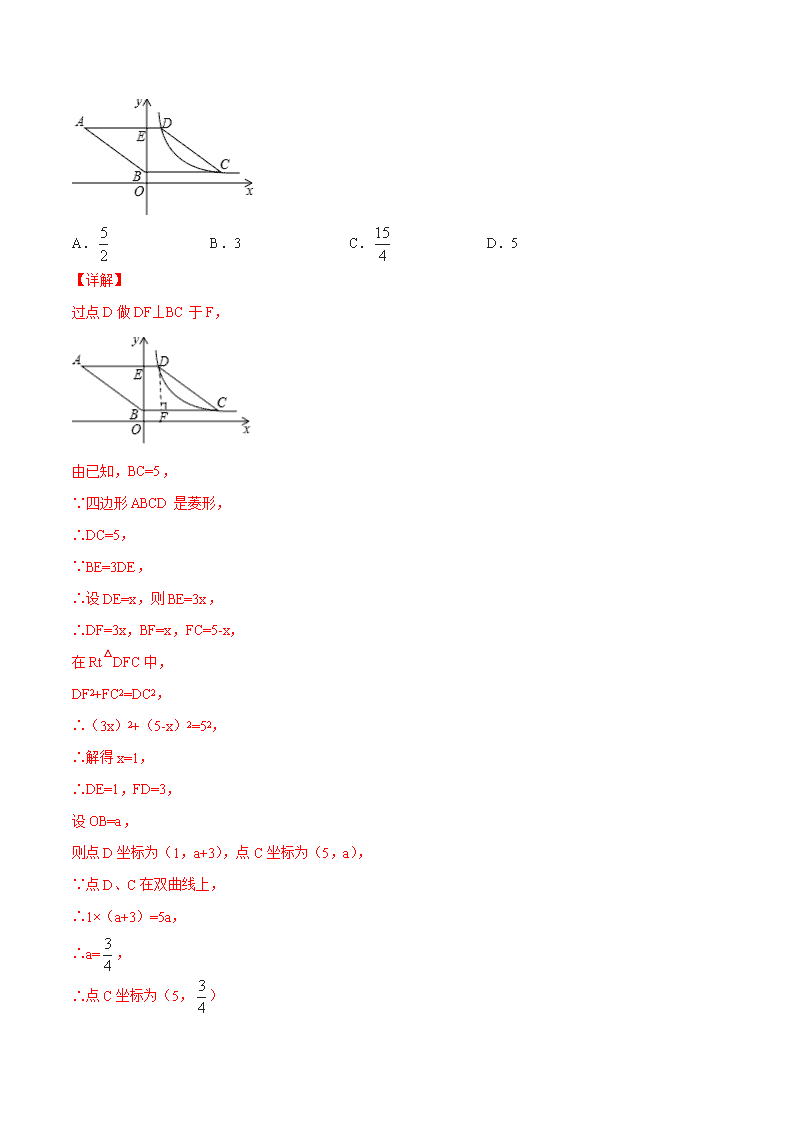
专题 14 反比例函数(专题测试-提高) 学校:___________姓名:___________班级:___________考号:___________ 一、选择题(共 12 小题,每题 4 分,共计 48 分) 1.(2018·云南中考模拟)如图,四边形 QABC 是矩形,ADEF 是正方形,点 A、D 在 x 轴的正半轴上,点 C 在 y 轴的正半轴上,点 F 在 AB 上,点 B、E 在反比例函数 y=kx 的图象上,OA=1,OC=6,则正方形 ADEF 的边长为( ) A.2 B.3 C.4 D.5 【详解】 ∵OA=1,OC=6, ∴B 点坐标为(1,6), ∴k=1×6=6, ∴反比例函数解析式为 y= 6 x , 设 AD=t,则 OD=1+t, ∴E 点坐标为(1+t,t), ∴(1+t)•t=6, 整理为 t2+t﹣6=0, 解得 t1=﹣3(舍去),t2=2, ∴正方形 ADEF 的边长为 2. 故选 A. 2.(2018·重庆中考真题)如图,菱形 ABCD 的边 AD⊥y 轴,垂足为点 E,顶点 A 在第二象限,顶点 B 在 y 轴的正半轴上,反比例函数 y= k x (k≠0,x>0)的图象同时经过顶点 C,D.若点 C 的横坐标为 5,BE=3DE, 则 k 的值为( ) A. 5 2 B.3 C. 15 4 D.5 【详解】 过点 D 做 DF⊥BC 于 F, 由已知,BC=5, ∵四边形 ABCD 是菱形, ∴DC=5, ∵BE=3DE, ∴设 DE=x,则 BE=3x, ∴DF=3x,BF=x,FC=5-x, 在 Rt △ DFC 中, DF2+FC2=DC2, ∴(3x)2+(5-x)2=52, ∴解得 x=1, ∴DE=1,FD=3, 设 OB=a, 则点 D 坐标为(1,a+3),点 C 坐标为(5,a), ∵点 D、C 在双曲线上, ∴1×(a+3)=5a, ∴a= 3 4 , ∴点 C 坐标为(5, 3 4 ) ∴k= 15 4 . 故选 C. 3.(2018·广西中考真题)如图,在同一平面直角坐标系中,一次函数 y1=kx+b(k、b 是常数,且 k≠0)与 反比例函数 y2= c x (c 是常数,且 c≠0)的图象相交于 A(﹣3,﹣2),B(2,3)两点,则不等式 y1>y2 的 解集是( ) A.﹣3<x<2 B.x<﹣3 或 x>2 C.﹣3<x<0 或 x>2 D.0<x<2 【详解】∵一次函数 y1=kx+b(k、b 是常数,且 k≠0)与反比例函数 y2= c x (c 是常数,且 c≠0)的图象相 交于 A(﹣3,﹣2),B(2,3)两点, ∴不等式 y1>y2 的解集是﹣3<x<0 或 x>2, 故选 C. 4.(2018·山东中考真题)已知反比例函数 y=﹣ 8 x ,下列结论:①图象必经过(﹣2,4);②图象在二,四 象限内;③y 随 x 的增大而增大;④当 x>﹣1 时,则 y>8.其中错误的结论有( )个 A.3 B.2 C.1 D.0 【详解】 ①当 x=﹣2 时,y=4,即图象必经过点(﹣2,4); ②k=﹣8<0,图象在第二、四象限内; ③k=﹣8<0,每一象限内,y 随 x 的增大而增大,错误; ④k=﹣8<0,每一象限内,y 随 x 的增大而增大,若 0>x>﹣1,﹣y>8,故④错误, 故选 B. 5.(2018·内蒙古中考真题)已知抛物线 y=x2+2x+k+1 与 x 轴有两个不同的交点,则一次函数 y=kx﹣k 与反 比例函数 y= k x 在同一坐标系内的大致图象是( ) A. B. C. D. 【详解】∵抛物线 y=x2+2x+k+1 与 x 轴有两个不同的交点, ∴△=4﹣4(k+1)>0, 解得 k<0, ∴一次函数 y=kx﹣k 的图象经过第一二四象限, 反比例函数 y= k x 的图象在第二四象限, 故选 D. 6.(2018·山东中考真题)若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线 y= k x (k<0)上,则 y1,y2,y3 的大小关系是( ) A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2 【详解】 ∵点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线 y= k x (k<0)上, ∴(﹣2,y1),(﹣1,y2)分布在第二象限,(3,y3)在第四象限,每个象限内,y 随 x 的增大而增大, ∴y3<y1<y2. 故选:D. 7.(2018·江苏中考真题)已知点 P(a,m),Q(b,n)都在反比例函数 y= 2 x 的图象上,且 a<0<b,则 下列结论一定正确的是( ) A.m+n<0 B.m+n>0 C.m<n D.m>n 【详解】 ∵y=− 2 x 的 k=-2<0,图象位于二四象限,a<0, ∴P(a,m)在第二象限, ∴m>0; ∵b>0, ∴Q(b,n)在第四象限, ∴n<0. ∴n<0<m, 即 m>n, 故 D 正确; 故选:D. 8.(2019·阳泉市中考模拟)函数 y1=x 和 y2= 1 x 的图象如图所示,则 y1>y2 的 x 取值范围是( ) A.x<﹣1 或 x>1 B.x<﹣1 或 0<x<1 C.﹣1<x<0 或 x>1 D.﹣1<x<0 或 0<x<1 【详解】 观察图象可知当﹣1<x<0 或 x>1 时,直线在双曲线的上方, 所以 y1>y2 的 x 取值范围是﹣1<x<0 或 x>1, 故选 C. 9.(2018·重庆中考真题)如图,在平面直角坐标系中,菱形 ABCD 的顶点 A,B 在反比例函数 ky x ( 0k , 0x )的图象上,横坐标分别为 1,4,对角线 BD x∥ 轴.若菱形 ABCD 的面积为 45 2 ,则 k 的值为( ) A. 5 4 B. 15 4 C.4 D.5 【详解】 设 A(1,m),B(4,n),连接 AC 交 BD 于点 M, 则有 BM=4-1=3,AM=m-n, ∴S 菱形 ABCD=4× 1 2 BM•AM, ∵S 菱形 ABCD= 45 2 , ∴4× 1 2 ×3(m-n)= 45 2 , ∴m-n= 15 4 , 又∵点 A,B 在反比例函数 ky x , ∴k=m=4n, ∴n= 5 4 , ∴k=4n=5, 故选 D. 10.(2018·吉林中考模拟)如图,点 A 在函数 y= 2 x (x>0)的图象上,点 B 在函数 y= 4 x (x>0)的图象 上,且 AB∥x 轴,BC⊥x 轴于点 C,则四边形 ABCO 的面积为( ) A.1 B.2 C.3 D.4 【详解】 延长 BA 交 y 轴与点 D, ∴ OADBCOD 4 1S S 四边形 , , ∴ ABCO 4 1 3S 四边形 ,故选 C. 11.(2018·辽宁中考真题)如图,菱形 ABCD 的边 AD 与 x 轴平行,A、B 两点的横坐标分别为 1 和 3,反 比例函数 y= 3 x 的图象经过 A、B 两点,则菱形 ABCD 的面积是( ) A.4 2 B.4 C.2 2 D.2 【详解】 如图,作 AH⊥BC 交 CB 的延长线于 H, ∵反比例函数 y= 3 x 的图象经过 A、B 两点,A、B 两点的横坐标分别为 1 和 3, ∴A、B 两点的纵坐标分别为 3 和 1,即点 A 的坐标为(1,3),点 B 的坐标为(3,1), ∴AH=3﹣1=2,BH=3﹣1=2, 由勾股定理得,AB= 2 22 2 2 2 , ∵四边形 ABCD 是菱形, ∴BC=AB=2 2 , ∴菱形 ABCD 的面积=BC×AH=4 2 , 故选 A. 12.(2018·山东中考真题)给出下列函数:①y=﹣3x+2;②y= 3 x ;③y=2x2;④y=3x,上述函数中符合条作 “当 x>1 时,函数值 y 随自变量 x 增大而增大“的是( ) A.①③ B.③④ C.②④ D.②③ 【详解】 ①y=﹣3x+2,当 x>1 时,函数值 y 随自变量 x 增大而减小,故此选项错误; ②y= 3 x ,当 x>1 时,函数值 y 随自变量 x 增大而减小,故此选项错误; ③y=2x2,当 x>1 时,函数值 y 随自变量 x 增大而减小,故此选项正确; ④y=3x,当 x>1 时,函数值 y 随自变量 x 增大而减小,故此选项正确. 故选 B. 二、填空题(共 5 小题,每题 4 分,共计 20 分) 13.(2018·江苏中考真题)如图,点 D 为矩形 OABC 的 AB 边的中点,反比例函数 ( 0)ky xx 的图象经过 点 D,交 BC 边于点 E.若 △ BDE 的面积为 1,则 k =________ 【详解】 设 D(a, k a ), ∵点 D 为矩形 OABC 的 AB 边的中点, ∴B(2a, k a ), ∴E(2a, 2 k a ), ∵△BDE 的面积为 1, ∴ 1 2 •a•( k a - 2 k a )=1,解得 k=4. 故答案为 4. 14.(2018·上海中考真题)已知反比例函数 y= 1k x (k 是常数,k≠1)的图象有一支在第二象限,那么 k 的取值范围是_____. 【详解】∵反比例函数 y= 1k x 的图象有一支在第二象限, ∴k﹣1<0, 解得 k<1, 故答案为:k<1. 15.(2018·浙江中考真题)如图,点 A,B 是反比例函数 y= k x (x>0)图象上的两点,过点 A,B 分别作 AC⊥x 轴于点 C,BD⊥x 轴于点 D,连接 OA,BC,已知点 C(2,0),BD=2,S △ BCD=3,则 S △ AOC=__. 【详解】 ∵BD⊥CD,BD=2, ∴S △ BCD= 1 2 BD•CD=3, 即 CD=3. ∵C(2,0), 即 OC=2, ∴OD=OC+CD=2+3=5, ∴B(5,2),代入反比例解析式得:k=10, 即 y=10 x , 则 S △ AOC=5. 故答案为:5. 16.(2018·合肥市中考模拟)如图,点 A 在双曲线 1y= x 上,点 B 在双曲线 3y= x 上,且 AB∥x 轴,C、D 在 x 轴上,若四边形 ABCD 为矩形,则它的面积为 . 【详解】 如图,过 A 点作 AE⊥y 轴,垂足为 E, ∵点 A 在双曲线 1y= x 上,∴四边形 AEOD 的面积为 1 ∵点 B 在双曲线 3y= x 上,且 AB∥x 轴,∴四边形 BEOC 的面积为 3 ∴四边形 ABCD 为矩形,则它的面积为 3-1=2 17.(2018·湖南中考真题)如图所示,点 A 是反比例函数 y= k x 图象上一点,作 AB⊥x 轴,垂足为点 B,若 △ AOB 的面积为 2,则 k 的值是_____. 【详解】∵点 A 是反比例函数 y= k x 图象上一点,作 AB⊥x 轴,垂足为点 B, ∴S △ AOB= 1 2 |k|=2, 又∵函数图象位于一、三象限, ∴k=4, 故答案为:4. 三、解答题(共 4 小题,每题 8 分,共计 32 分) 18.(2017·四川中考真题)已知 A(﹣4,2)、B(n,﹣4)两点是一次函数 y=kx+b 和反比例函数 y= m x 图 象的两个交点. (1)求一次函数和反比例函数的解析式; (2)求 △ AOB 的面积; (3)观察图象,直接写出不等式 kx+b﹣ m x >0 的解集. 【答案】(1)反比例函数解析式为 y=﹣ 8 x ,一次函数的解析式为 y=﹣x﹣2;(2)6;(3)x<﹣4 或 0<x <2. 【名师点拨】 (1)先把点 A 的坐标代入反比例函数解析式,即可得到 m=﹣8,再把点 B 的坐标代入反比例函数解析式, 即可求出 n=2,然后利用待定系数法确定一次函数的解析式; (2)先求出直线 y=﹣x﹣2 与 x 轴交点 C 的坐标,然后利用 S △ AOB=S △ AOC+S △ BOC 进行计算; (3)观察函数图象得到当 x<﹣4 或 0<x<2 时,一次函数的图象在反比例函数图象上方,据此可得不等 式的解集. 【详解】 (1)把 A(﹣4,2)代入 ,得 m=2×(﹣4)=﹣8,所以反比例函数解析式为 ,把 B(n, ﹣4)代入 ,得﹣4n=﹣8,解得 n=2,把 A(﹣4,2)和 B(2,﹣4)代入 y=kx+b,得: , 解得: ,所以一次函数的解析式为 y=﹣x﹣2; (2)y=﹣x﹣2 中,令 y=0,则 x=﹣2,即直线 y=﹣x﹣2 与 x 轴交于点 C(﹣2,0),∴ S △ AOB=S △ AOC+S △ BOC= ×2×2+ ×2×4=6; (3)由图可得,不等式 的解集为:x<﹣4 或 0<x<2. 19.(2018·黑龙江中考真题)如图,A(4,3)是反比例函数 y= k x 在第一象限图象上一点,连接 OA,过 A 作 AB∥x 轴,截取 AB=OA(B 在 A 右侧),连接 OB,交反比例函数 y= k x 的图象于点 P. (1)求反比例函数 y= k x 的表达式; (2)求点 B 的坐标; (3)求 △ OAP 的面积. 【名师点拨】(1)将点 A 的坐标代入解析式求解可得; (2)利用勾股定理求得 AB=OA=5,由 AB∥x 轴即可得点 B 的坐标; (3)先根据点 B 坐标得出 OB 所在直线解析式,从而求得直线与双曲线交点 P 的坐标,再利用割 补法求解可得. 【详解】(1)将点 A(4,3)代入 y= k x ,得:k=12, 则反比例函数解析式为 y=12 x ; (2)如图,过点 A 作 AC⊥x 轴于点 C, 则 OC=4、AC=3, ∴OA= 2 24 3 =5, ∵AB∥x 轴,且 AB=OA=5, ∴点 B 的坐标为(9,3); (3)∵点 B 坐标为(9,3), ∴OB 所在直线解析式为 y= 1 3 x, 由 1 3 12 y x y x 可得点 P 坐标为(6,2),(负值舍去), 过点 P 作 PD⊥x 轴,延长 DP 交 AB 于点 E, 则点 E 坐标为(6,3), ∴AE=2、PE=1、PD=2, 则 △ OAP 的面积= 1 2 ×(2+6)×3﹣ 1 2 ×6×2﹣ 1 2 ×2×1=5. 20.(2018·甘肃中考真题)如图,一次函数 y=x+4 的图象与反比例函数 y= k x (k 为常数且 k≠0)的图象交 于 A(﹣1,a),B 两点,与 x 轴交于点 C. (1)求此反比例函数的表达式; (2)若点 P 在 x 轴上,且 S △ ACP= 3 2 S △ BOC,求点 P 的坐标. 【名师点拨】 (1)利用点 A 在 y=﹣x+4 上求 a,进而代入反比例函数 ky x 求 k. (2)联立方程求出交点,设出点 P 坐标表示三角形面积,求出 P 点坐标. 【详解】 (1)把点 A(﹣1,a)代入 y=x+4,得 a=3, ∴A(﹣1,3) 把 A(﹣1,3)代入反比例函数 ky x ∴k=﹣3, ∴反比例函数的表达式为 3 .y x (2)联立两个函数的表达式得 4y x ky x 解得 1 3 x y 或 3 1 x y ∴点 B 的坐标为 B(﹣3,1) 当 y=x+4=0 时,得 x=﹣4 ∴点 C(﹣4,0) 设点 P 的坐标为(x,0) ∵ 3 2ACP BOCS SV V , ∴ 1 3 13 4 4 1,2 2 2x 解得 x1=﹣6,x2=﹣2 ∴点 P(﹣6,0)或(﹣2,0) 21.(2018·四川中考真题)某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如 图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度 y (℃)与时间 x(h)之间的函数关系,其 中线段 AB、BC 表示恒温系统开启阶段,双曲线的一部分 CD 表示恒温系统关闭阶段. 请根据图中信息解答下列问题: (1)求这天的温度 y 与时间 x(0≤x≤24)的函数关系式; (2)求恒温系统设定的恒定温度; (3)若大棚内的温度低于 10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使 蔬菜避免受到伤害? 【名师点拨】 (1)应用待定系数法分段求函数解析式; (2)观察图象可得; (3)代入临界值 y=10 即可. 【详解】 (1)设线段 AB 解析式为 y=k1x+b(k≠0) ∵线段 AB 过点(0,10),(2,14) 代入得 1 10 2 14 b k b = = 解得 1 2 10 k b = = ∴AB 解析式为:y=2x+10(0≤x<5) ∵B 在线段 AB 上当 x=5 时,y=20 ∴B 坐标为(5,20) ∴线段 BC 的解析式为:y=20(5≤x<10) 设双曲线 CD 解析式为:y= 2k x (k2≠0) ∵C(10,20) ∴k2=200 ∴双曲线 CD 解析式为:y= 200 x (10≤x≤24) ∴y 关于 x 的函数解析式为: 2 10(0 5) 20(5 10) 200 10 24 x x y x xx (2)由(1)恒温系统设定恒温为 20°C (3)把 y=10 代入 y= 200 x 中,解得,x=20 ∴20-10=10 答:恒温系统最多关闭 10 小时,蔬菜才能避免受到伤害.查看更多