九年级数学上册第23章图形的相似23-3相似三角形第2课时学案新版华东师大版

九年级数学上册第23章图形的相似23-3相似三角形第2课时学案新版华东师大版

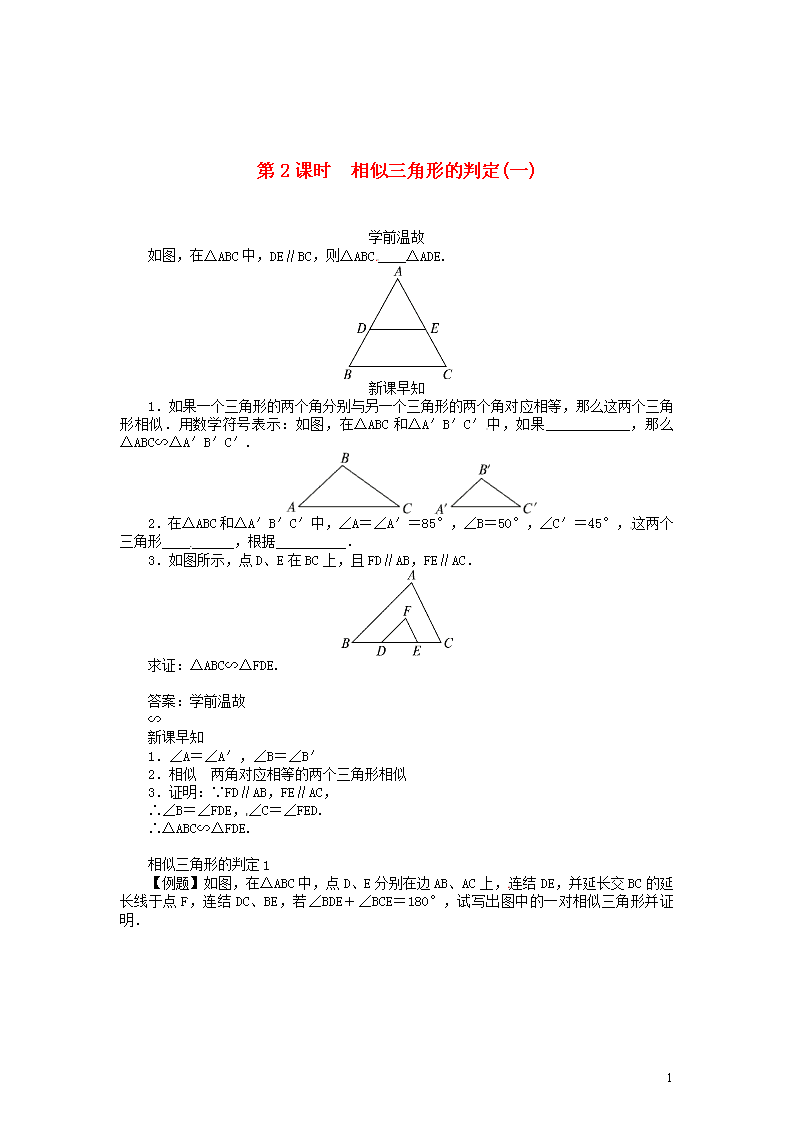
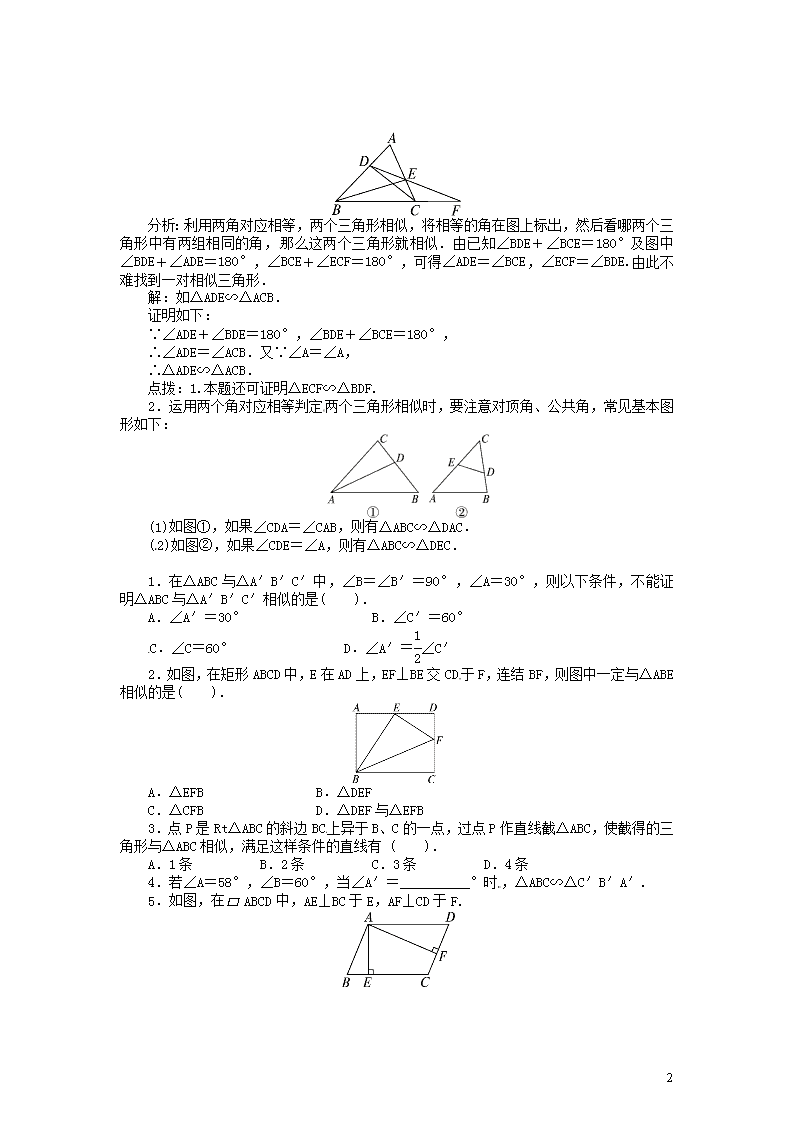
第2课时　相似三角形的判定(一)‎ 学前温故 如图，在△ABC中，DE∥BC，则△ABC____△ADE.‎ 新课早知 ‎1．如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似．用数学符号表示：如图，在△ABC和△A′B′C′中，如果____________，那么△ABC∽△A′B′C′.‎ ‎2．在△ABC和△A′B′C′中，∠A＝∠A′＝85°，∠B＝50°，∠C′＝45°，这两个三角形__________，根据__________．‎ ‎3．如图所示，点D、E在BC上，且FD∥AB，FE∥AC．‎ 求证：△ABC∽△FDE.‎ 答案：学前温故 ‎∽‎ 新课早知 ‎1．∠A＝∠A′，∠B＝∠B′‎ ‎2．相似　两角对应相等的两个三角形相似 ‎3．证明：∵FD∥AB，FE∥AC，‎ ‎∴∠B＝∠FDE，∠C＝∠FED.‎ ‎∴△ABC∽△FDE.‎ 相似三角形的判定1‎ ‎【例题】 如图，在△ABC中，点D、E分别在边AB、AC上，连结DE，并延长交BC的延长线于点F，连结DC、BE，若∠BDE＋∠BCE＝180°，试写出图中的一对相似三角形并证明．‎ 3‎ 分析：利用两角对应相等，两个三角形相似，将相等的角在图上标出，然后看哪两个三角形中有两组相同的角，那么这两个三角形就相似．由已知∠BDE＋∠BCE＝180°及图中∠BDE＋∠ADE＝180°，∠BCE＋∠ECF＝180°，可得∠ADE＝∠BCE，∠ECF＝∠BDE.由此不难找到一对相似三角形．‎ 解：如△ADE∽△ACB．‎ 证明如下：‎ ‎∵∠ADE＋∠BDE＝180°，∠BDE＋∠BCE＝180°，‎ ‎∴∠ADE＝∠ACB．又∵∠A＝∠A，‎ ‎∴△ADE∽△ACB．‎ 点拨：1.本题还可证明△ECF∽△BDF.‎ ‎2．运用两个角对应相等判定两个三角形相似时，要注意对顶角、公共角，常见基本图形如下：‎ ‎(1)如图①，如果∠CDA＝∠CAB，则有△ABC∽△DAC．‎ ‎(2)如图②，如果∠CDE＝∠A，则有△ABC∽△DEC．‎ ‎1．在△ABC与△A′B′C′中，∠B＝∠B′＝90°，∠A＝30°，则以下条件，不能证明△ABC与△A′B′C′相似的是(　　)．‎ A．∠A′＝30° B．∠C′＝60°‎ C．∠C＝60° D．∠A′＝∠C′‎ ‎2．如图，在矩形ABCD中，E在AD上，EF⊥BE交CD于F，连结BF，则图中一定与△ABE相似的是(　　)．‎ A．△EFB B．△DEF C．△CFB D．△DEF与△EFB ‎3．点P是Rt△ABC的斜边BC上异于B、C的一点，过点P作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线有 (　　)．‎ A．1条 B．2条 C．3条 D．4条 ‎4．若∠A＝58°，∠B＝60°，当∠A′＝__________°时，△ABC∽△C′B′A′.‎ ‎5．如图，在ABCD中，AE⊥BC于E，AF⊥CD于F.‎ 3‎ 求证：△ABE∽△ADF.‎ ‎6．如图所示，已知△ABC与△ADE的边BC、AD相交于O，且∠1＝∠2，∠B＝∠D．‎ 求证：(1)△ABO∽△CDO；‎ ‎(2)△ABC∽△ADE.‎ 答案：1．C　2.B ‎3．C　过点P分别作三角形三边的垂线，所得三角形与原三角形相似．‎ ‎4．62‎ ‎5．证明：∵AE⊥BC，AF⊥CD，‎ ‎∴∠AEB＝∠AFD＝90°.‎ 又∵四边形ABCD是平行四边形，∴∠B＝∠D.‎ ‎∴△ABE∽△ADF.‎ ‎6．证明：(1)∵∠B＝∠D，∠AOB＝∠COD，‎ ‎∴△ABO∽△CDO.‎ ‎(2)∵∠1＝∠2，‎ ‎∴∠BAC＝∠DAE.‎ 又∠B＝∠D，‎ ‎∴△ABC∽△ADE.‎ 3‎