2020年四川省自贡市中考数学试卷【word版本；可编辑；含答案】

2020年四川省自贡市中考数学试卷【word版本；可编辑；含答案】

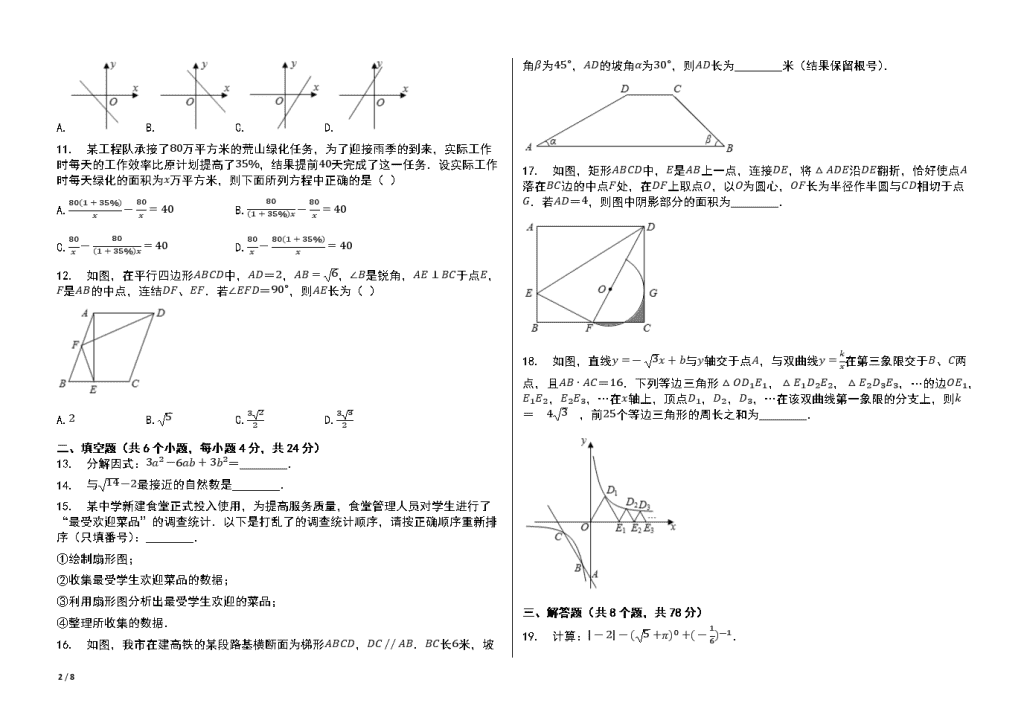
‎2020年四川省自贡市中考数学试卷 一．选择题（共12个小题，每小题4分，共48分，在每题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1. 如图，直线a // b，‎∠1‎＝‎50‎‎∘‎，则‎∠2‎的度数为（ ）‎ A.‎40‎‎∘‎ B.‎50‎‎∘‎ C.‎55‎‎∘‎ D.‎‎60‎‎∘‎ ‎2. ‎5‎月‎22‎日晚，中国自贡第‎26‎届国际恐龙灯会开启网络直播，有着近千年历史的自贡灯会进入“云游”时代，‎70‎余万人通过“云观灯”感受了“天下第一灯”的璀璨．人数‎700000‎用科学记数法表示为（ ）‎ A.‎70×‎‎10‎‎4‎ B.‎0.7×‎‎10‎‎7‎ C.‎7×‎‎10‎‎5‎ D.‎‎7×‎‎10‎‎6‎ ‎3. 如图所示的几何体的左视图是（ ）‎ A. B. C. D.‎ ‎4. 关于x的一元二次方程ax‎2‎-2x+2‎＝‎0‎有两个相等实数根，则a的值为（ ）‎ A.‎1‎‎2‎ B.‎-‎‎1‎‎2‎ C.‎1‎ D.‎‎-1‎ ‎5. 在平面直角坐标系中，将点‎(2, 1)‎向下平移‎3‎个单位长度，所得点的坐标是（ ）‎ A.‎(-1, 1)‎ B.‎(5, 1)‎ C.‎(2, 4)‎ D.‎‎(2, -2)‎ ‎6. 下列图形中，是轴对称图形，但不是中心对称图形的是（ ）‎ A. B.‎ C. D.‎ ‎7. 对于一组数据‎3‎，‎7‎，‎5‎，‎3‎，‎2‎，下列说法正确的是（ ）‎ A.中位数是‎5‎ B.众数是‎7‎ C.平均数是‎4‎ D.方差是‎3‎ ‎8. 如果一个角的度数比它补角的‎2‎倍多‎30‎‎∘‎，那么这个角的度数是（ ）‎ A.‎50‎‎∘‎ B.‎70‎‎∘‎ C.‎130‎‎∘‎ D.‎‎160‎‎∘‎ ‎9. 如图，在Rt△ABC中，‎∠ACB＝‎90‎‎∘‎，‎∠A＝‎50‎‎∘‎，以点B为圆心，BC长为半径画弧，交AB于点D，连接CD，则‎∠ACD的度数是（ ）‎ A.‎50‎‎∘‎ B.‎40‎‎∘‎ C.‎30‎‎∘‎ D.‎‎20‎‎∘‎ ‎10. 函数y=‎kx与y＝ax‎2‎+bx+c的图象如图所示，则函数y＝kx-b的大致图象为（ ）‎ ‎ 8 / 8‎ A. B. C. D.‎ ‎11. 某工程队承接了‎80‎万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了‎35%‎，结果提前‎40‎天完成了这一任务．设实际工作时每天绿化的面积为x万平方米，则下面所列方程中正确的是（ ）‎ A.‎80(1+35%)‎x‎-‎80‎x=40‎ B.‎‎80‎‎(1+35%)x‎-‎80‎x=40‎ C.‎80‎x‎-‎80‎‎(1+35%)x=40‎ D.‎‎80‎x‎-‎80(1+35%)‎x=40‎ ‎12. 如图，在平行四边形ABCD中，AD＝‎2‎，AB=‎‎6‎，‎∠B是锐角，AE⊥BC于点E，F是AB的中点，连结DF、EF．若‎∠EFD＝‎90‎‎∘‎，则AE长为（ ）‎ A.‎2‎ B.‎5‎ C.‎3‎‎2‎‎2‎ D.‎‎3‎‎3‎‎2‎ 二、填空题（共6个小题，每小题4分，共24分）‎ ‎13. 分解因式：‎3a‎2‎-6ab+3‎b‎2‎＝________．‎ ‎14. 与‎14‎‎-2‎最接近的自然数是________．‎ ‎15. 某中学新建食堂正式投入使用，为提高服务质量，食堂管理人员对学生进行了“最受欢迎菜品”的调查统计．以下是打乱了的调查统计顺序，请按正确顺序重新排序（只填番号）：________．‎ ‎①绘制扇形图；‎ ‎②收集最受学生欢迎菜品的数据；‎ ‎③利用扇形图分析出最受学生欢迎的菜品；‎ ‎④整理所收集的数据．‎ ‎16. 如图，我市在建高铁的某段路基横断面为梯形ABCD，DC // AB．BC长‎6‎米，坡角β为‎45‎‎∘‎，AD的坡角α为‎30‎‎∘‎，则AD长为________米（结果保留根号）．‎ ‎17. 如图，矩形ABCD中，E是AB上一点，连接DE，将‎△ADE沿DE翻折，恰好使点A落在BC边的中点F处，在DF上取点O，以O为圆心，OF长为半径作半圆与CD相切于点G．若AD＝‎4‎，则图中阴影部分的面积为________．‎ ‎18. 如图，直线y=-‎3‎x+b与y轴交于点A，与双曲线y=‎kx在第三象限交于B、C两点，且AB⋅AC＝‎16‎．下列等边三角形‎△OD‎1‎E‎1‎，‎△‎E‎1‎D‎2‎E‎2‎，‎△‎E‎2‎D‎3‎E‎3‎，…的边OE‎1‎，E‎1‎E‎2‎，E‎2‎E‎3‎，…在x轴上，顶点D‎1‎，D‎2‎，D‎3‎，…在该双曲线第一象限的分支上，则k＝ ‎4‎‎3‎ ，前‎25‎个等边三角形的周长之和为________．‎ ‎ 8 / 8‎ 三、解答题（共8个题，共78分）‎ ‎19. 计算：‎|-2|-(‎5‎+π‎)‎‎0‎+(-‎‎1‎‎6‎‎)‎‎-1‎．‎ ‎20. 先化简，再求值：x+1‎x‎2‎‎-4‎‎⋅(‎1‎x+1‎+1)‎，其中x是不等式组x+1≥0‎‎5-2x>3‎‎ ‎的整数解．‎ ‎21. 如图，在正方形ABCD中，点E在BC边的延长线上，点F在CD边的延长线上，且CE＝DF，连接AE和BF相交于点M．‎ 求证：AE＝BF．‎ ‎22. 某校为了响应市政府号召，在“创文创卫”活动周中，设置了“A：文明礼仪，B：环境保护，C：卫生保洁，D：垃圾分类”四个主题，每个学生选一个主题参与．为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如图条形统计图和扇形统计图．‎ ‎（1）本次调查的学生人数是________人，m＝________；‎ ‎（2）请补全条形统计图；‎ ‎（3）学校要求每位同学从星期一至星期五选择两天参加活动．如果小张同学随机选择连续两天，其中有一天是星期一的概率是________；小李同学星期五要参加市演讲比赛，他在其余四天中随机选择两天，其中有一天是星期三的概率是________．‎ ‎ 8 / 8‎ ‎23. 甲、乙两家商场平时以同样价格出售相同的商品．新冠疫情期间，为了减少库存，甲、乙两家商场打折促销．甲商场所有商品按‎9‎折出售，乙商场对一次购物中超过‎100‎元后的价格部分打‎8‎折．‎ ‎（1）以x（单位：元）表示商品原价，y（单位：元）表示实际购物金额，分别就两家商场的让利方式写出y关于x的函数解析式；‎ ‎（2）新冠疫情期间如何选择这两家商场去购物更省钱？‎ ‎24. 我国著名数学家华罗庚说过“数缺形时少直观，形少数时难入微”，数形结合是解决数学问题的重要思想方法．例如，代数式‎|x-2|‎的几何意义是数轴上x所对应的点与‎2‎所对应的点之间的距离：因为‎|x+1|‎＝‎|x-(-1)|‎，所以‎|x+1|‎的几何意义就是数轴上x所对应的点与‎-1‎所对应的点之间的距离．‎ ‎（1）发现问题：代数式‎|x+1|+|x-2|‎的最小值是多少？‎ ‎（2）探究问题：如图，点A、B、P分别表示数‎-1‎、‎2‎、x，AB＝‎3‎．‎ ‎∵ ‎|x+1|+|x-2|‎的几何意义是线段PA与PB的长度之和，‎ ‎∴ 当点P在线段AB上时，PA+PB＝‎3‎，当点P在点A的左侧或点B的右侧时，PA+PB>3‎．‎ ‎∴ ‎|x+1|+|x-2|‎的最小值是‎3‎．‎ ‎（3）解决问题：‎ ‎①‎|x-4|+|x+2|‎的最小值是________；‎ ‎②利用上述思想方法解不等式：‎|x+3|+|x-1|>4‎；‎ ‎③当a为何值时，代数式‎|x+a|+|x-3|‎的最小值是‎2‎．‎ ‎ 8 / 8‎ ‎25. 如图，‎⊙O是‎△ABC的外接圆，AB为直径，点P为‎⊙O外一点，且PA＝PC=‎2‎AB，连接PO交AC于点D，延长PO交‎⊙O于点F．‎ ‎（1）证明：AF‎=‎CF；‎ ‎（2）若tan∠ABC＝‎2‎‎2‎，证明：PA是‎⊙O的切线；‎ ‎（3）在（2）条件下，连接PB交‎⊙O于点E，连接DE，若BC＝‎2‎，求DE的长．‎ ‎26. 在平面直角坐标系中，抛物线y＝ax‎2‎+bx+3‎与x轴交于点A(-3, 0)‎、B(1, 0)‎，交y轴于点N，点M为抛物线的顶点，对称轴与x轴交于点C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图‎1‎，连接AM，点E是线段AM上方抛物线上一动点，EF⊥AM于点F，过点E作EH⊥x轴于点H，交AM于点D．点P是y轴上一动点，当EF取最大值时：‎ ‎①求PD+PC的最小值；‎ ‎②如图‎2‎，Q点为y轴上一动点，请直接写出DQ+‎1‎‎4‎OQ的最小值．‎ ‎ 8 / 8‎ 参考答案与试题解析 ‎2020年四川省自贡市中考数学试卷 一．选择题（共12个小题，每小题4分，共48分，在每题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.B 2.C 3.B 4.A 5.D ‎ ‎6.A 7.C 8.C 9.D 10.D ‎ ‎11.A 12.B 二、填空题（共6个小题，每小题4分，共24分）‎ ‎13.‎3(a-b‎)‎‎2‎ 14.‎‎2‎ ‎15.②④①③ 16.‎‎6‎‎2‎ ‎17.‎2‎‎3‎‎9‎ 18.‎‎60‎ 三、解答题（共8个题，共78分）‎ ‎19.原式＝‎‎2-1+(-6)‎ ‎＝‎‎1+(-6)‎ ‎＝‎-5‎．‎ ‎20.‎x+1‎x‎2‎‎-4‎‎⋅(‎1‎x+1‎+1)‎ ‎=x+1‎‎(x+2)(x-2)‎⋅‎‎1+x+1‎x+1‎ ‎=‎x+2‎‎(x+2)(x-2)‎ ‎=‎‎1‎x-2‎‎，‎ 由不等式组x+1≥0‎‎5-2x>3‎‎ ‎，得‎-1≤x<1‎，‎ ‎∵ x是不等式组x+1≥0‎‎5-2x>3‎‎ ‎的整数解，‎ ‎∴ x＝‎-1‎，‎0‎，‎ ‎∵ 当x＝‎-1‎时，原分式无意义，‎ ‎∴ x＝‎0‎，‎ 当x＝‎0‎时，原式‎=‎1‎‎0-2‎=-‎‎1‎‎2‎．‎ ‎21.在正方形ABCD中，‎ AB‎＝CD＝CD＝AD，‎ ‎∵ CE＝DF，‎ ‎∴ BE＝CF，‎ 在‎△AEB与‎△BFC中，‎ AB=BC‎∠ABE=∠BCFBE=CF‎ ‎‎，‎ ‎∴ ‎△AEB≅△BFC(SAS)‎，‎ ‎∴ AE＝BF．‎ ‎22.‎60‎,‎‎30‎ C组的人数为‎60-18-12-9‎＝‎21‎（人），补全条形统计图如图：‎ ‎1‎‎4‎‎,‎‎1‎‎2‎ ‎23.由题意可得，‎ y甲‎＝‎0.9x，‎ 当‎0≤x≤100‎时，y乙＝x，‎ 当x>100‎时，y乙＝‎100+(x-100)×0.8‎＝‎0.8x+20‎，‎ 由上可得，y乙‎=x‎(0≤x≤100)‎‎0.8x+20‎‎(x>100)‎ ‎；‎ 当‎0.9x<0.8x+20‎时，得x<200‎，即此时选择甲商场购物更省钱；‎ 当‎0.9x＝‎0.8x+20‎时，得x＝‎200‎，即此时两家商场购物一样；‎ 当‎0.9x>0.8x+200‎时，得x>200‎，即此时选择乙商场购物更省钱．‎ ‎24.②如图所示，满足‎|x+3|+|x-1|>4‎的x范围为x<-3‎或x>1‎ ‎③当a为‎-1‎或‎-5‎时，代数式‎|x+a|+|x-3|‎的最小值是‎2‎ ‎6‎ ‎25.证明：连接OC．‎ ‎ 8 / 8‎ ‎∵ PC＝PA，OC＝OA，‎ ‎∴ OP垂直平分线段AC，‎ ‎∴ AF‎=‎CF．‎ 证明：设BC＝a，‎ ‎∵ AB是直径，‎ ‎∴ ‎∠ACB＝‎90‎‎∘‎，‎ ‎∵ tan∠ABC=ACBC=2‎‎2‎，‎ ‎∴ AC＝‎2‎2‎a，AB=BC‎2‎+AC‎2‎=a‎2‎‎+(2‎2‎a‎)‎‎2‎=3a，‎ ‎∴ OC＝OA＝OB=‎‎3a‎2‎，CD＝AD=‎2‎a，‎ ‎∵ PA＝PC=‎2‎AB，‎ ‎∴ PA＝PC＝‎3‎2‎a，‎ ‎∵ ‎∠PDC＝‎90‎‎∘‎，‎ ‎∴ PD=PC‎2‎-CD‎2‎=‎18a‎2‎-2‎a‎2‎=4a，‎ ‎∵ DC＝DA，AO＝OB，‎ ‎∴ OD=‎1‎‎2‎BC=‎1‎‎2‎a，‎ ‎∴ AD‎2‎＝PD⋅OD，‎ ‎∴ ADPD‎=‎ODAD，‎ ‎∵ ‎∠ADP＝‎∠ADO＝‎90‎‎∘‎，‎ ‎∴ ‎△ADP∽△ODA，‎ ‎∴ ‎∠PAD＝‎∠DOA，‎ ‎∵ ‎∠DOA+∠DAO＝‎90‎‎∘‎，‎ ‎∴ ‎∠PAD+∠DAO＝‎90‎‎∘‎，‎ ‎∴ ‎∠PAO＝‎90‎‎∘‎，‎ ‎∴ OA⊥PA，‎ ‎∴ PA是‎⊙O的切线．‎ 如图，过点E作EJ⊥PF于J，BK⊥PF于K．‎ ‎∵ BC＝‎2‎，‎ 由（1）可知，PA＝‎6‎‎2‎，AB＝‎6‎，‎ ‎∵ ‎∠PAB＝‎90‎‎∘‎，‎ ‎∴ PB=PA‎2‎+AB‎2‎=‎72+36‎=6‎‎3‎，‎ ‎∵ PA‎2‎＝PE⋅PB，‎ ‎∴ PE=‎72‎‎6‎‎3‎=4‎‎3‎，‎ ‎∵ ‎∠CDK＝‎∠BKD＝‎∠BCD＝‎90‎‎∘‎，‎ ‎∴ 四边形CDKB是矩形，‎ ‎∴ CD＝BK＝‎2‎‎2‎，BC＝DK＝‎2‎，‎ ‎∵ PD＝‎8‎，‎ ‎∴ PK＝‎10‎，‎ ‎∵ EJ // BK，‎ ‎∴ PEPB‎=EJBK=‎PJPK，‎ ‎∴ ‎4‎‎3‎‎6‎‎3‎‎=EJ‎2‎‎2‎=‎PJ‎10‎，‎ ‎∴ EJ=‎‎4‎‎2‎‎3‎，PJ=‎‎20‎‎3‎，‎ ‎∴ DJ＝PD-PJ＝‎8-‎20‎‎3‎=‎‎4‎‎3‎，‎ ‎∴ DE=EJ‎2‎+DJ‎2‎=‎(‎4‎‎2‎‎3‎‎)‎‎2‎+(‎‎4‎‎3‎‎)‎‎2‎=‎‎4‎‎3‎‎3‎．‎ ‎26.抛物线的表达式为：y＝a(x+3)(x-1)‎＝a(x‎2‎+2x-3)‎＝ax‎2‎+2ax-3a，‎ 即‎-3a＝‎3‎，解得：a＝‎-1‎，‎ 故抛物线的表达式为：y＝‎-x‎2‎-2x+3‎；‎ ‎ 8 / 8‎ 由抛物线的表达式得，点M(-1, 4)‎，点N(0, 3)‎，‎ 则tan∠MAC=MCAC=2‎，‎ 则设直线AM的表达式为：y＝‎2x+b，‎ 将点A的坐标代入上式并解得：b＝‎6‎，‎ 故直线AM的表达式为：y＝‎2x+6‎，‎ ‎∵ ‎∠EFD＝‎∠DHA＝‎90‎‎∘‎，‎∠EDF＝‎∠ADH，‎ ‎∴ ‎∠MAC＝‎∠DEF，则tan∠DEF＝‎2‎，则cos∠DEF=‎‎5‎‎5‎，‎ 设点E(x, -x‎2‎-2x+3)‎，则点D(x, 2x+6)‎，‎ 则FE＝EDcos∠DEF＝‎(-x‎2‎-2x+3-2x-6)×‎5‎‎5‎=‎5‎‎5‎(-x‎2‎-4x-3)‎，‎ ‎∵ ‎-‎5‎‎5‎<0‎，故EF有最大值，此时x＝‎-2‎，故点D(-2, 2)‎；‎ ‎①点C(-1, 0)‎关于y轴的对称点为点B(1, 0)‎，连接BD交y轴于点P，则点P为所求点，‎ PD+PC‎＝PD+PB＝DB为最小，‎ 则BD=‎(1+2‎)‎‎2‎+(0-2‎‎)‎‎2‎=‎‎13‎；‎ ‎②过点O作直线OK，使sin∠NOK=‎‎1‎‎4‎，过点D作DK⊥OK于点K，交y轴于点Q，则点Q为所求点，‎ DQ+‎1‎‎4‎OQ‎＝DQ+QK＝DK为最小值，‎ 则直线OK的表达式为：y=‎15‎x，‎ ‎∵ DK⊥OK，故设直线DK的表达式为：y=-‎1‎‎15‎x+b，‎ 将点D的坐标代入上式并解得：b＝‎2-‎‎2‎‎15‎，‎ 则直线DK的表达式为：y=-‎1‎‎15‎x+2-‎‎2‎‎15‎，‎ 故点Q(0, 2-‎2‎‎15‎)‎，‎ 由直线KD的表达式知，QD与x负半轴的夹角（设为α）的正切值为‎1‎‎15‎，则cosα=‎‎15‎‎4‎，‎ 则DQ=xQ‎-‎xDcosα=‎2‎‎15‎‎4‎=‎‎8‎‎15‎，而‎1‎‎4‎OQ=‎1‎‎4‎(2-‎2‎‎15‎)‎，‎ 则DQ+‎1‎‎4‎OQ为最小值‎=‎8‎‎15‎+‎1‎‎4‎(2-‎2‎‎15‎)=‎‎15‎‎+1‎‎2‎．‎ ‎ 8 / 8‎