- 2021-11-10 发布 |
- 37.5 KB |
- 33页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级数学上册第四章图形的相似小结与复习课件新版北师大版
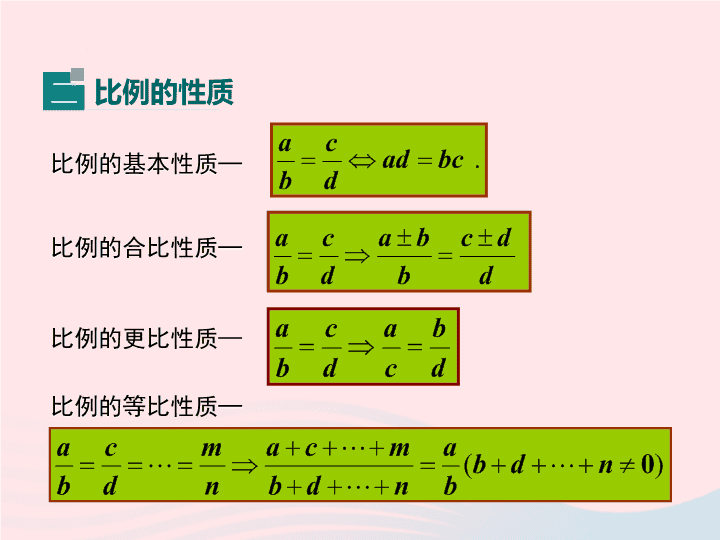
小结与复习 第四章 图形的相似 导入新课 讲授新课 当堂练习 课堂小结 线段的比和成比例线段的定义 一 如果选用一个长度单位量得两条线段 a , b 的长度分别为 m , n . 那么 两条线段的比 . 四条线段 a , b , c , d 中,如果 a 与 b 的比等于 c 与 d 的比,那么这四条线段 a , b , c , d 叫做成 比例线段 ,简称 比例线段 . 要点梳理 比例的基本性质 ─ 比例的 合比性质 ─ 比例的 等比性质 ─ 比例的更比性质 — 比例的性质 二 点 C 把线段 AB 分成两条线段 AC 和 BC ,如果 A C B 那么称线段 AB 被点 C 点 C 叫做线段 AB 的 AC 与 AB (或 BC 与 AC ) 的比叫做 黄金比 ≈ 0.618 黄金分割 黄金分割点 黄金比 黄金分割 三 1. 定义: 三角对应角相等、三边对应成比例的两个三角形叫相似三角形 . 相似三角形的定义、判定、性质 四 2. 判定定理: ( 1 )两角相等的两个三角形相似 ( 2 )三边对应成比例的两个三角形相似 ( 3 ) 两边对应成比例且夹角相等的两个三角形相似 3. 性质: ( 1 )相似三角形对应角相等,对应边成比例 ( 2 )相似三角形对应高的比,对应角平分线的比和对应中线的 比都等于相似比 ★相似三角形周长的比等于 相似比 ★相似三角形面积的比等于 相似比的平方 ★相似多边形的周长比等于 相似比 ★相似多边形面积的比等于 相似比的平方 相似三角形的应用 五 ( 1 ) 测高 测量不能到达两点间的距离 , 常构造相似三角形求解 . (不能直接使用皮尺或刻度尺量的) (不能直接测量的两点间的距离) 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决 . ( 2 ) 测距 例如用相似测物体的高度 A B C E D 1.6m 8.4m 1.2m 测山高 测楼高 测内孔直径 A B D E F G H 求最大值与最小值 C 如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形 . ★ 这个点叫做 位似中心 . ★ 这两个相似图形的相似比又称为 位似比 . ★位似图形上任意一对对应点到位似中心的距离之比等于 位似比 . 图形的位似 六 3. 体会位似图形何时为 正像 何时为 倒像 . 2. 如何作位似图形 ( 缩小 ) . O P 1. 如何作位似图形 ( 放大 ) . A B G C E D F ● P B ′ A ′ C ′ D ′ E ′ F ′ G ′ A ′ B ′ C ′ D ′ E ′ F ′ G ′ A B G C E D F ● P 位似图形的作法 七 考点一 成比例线段、比例的性质和黄金分割 考点讲练 例 1 下列各组不同长度的线段是成比例线段的是 ( ) A . 3 cm , 6 cm , 7 cm , 9 cm B . 2 cm , 5 cm , 0.6 dm , 8 cm C . 3 cm , 9 cm , 1.8 dm , 6 cm D . 1 cm, 2 cm, 3 cm, 4 cm 解析: 根据成比例线段的定义,对各选项进行一一分析. A. 故不是成比例线段; B . 0.6 dm = 6 cm , 故不是成比例线段; C . 1.8 dm = 18 cm ,从小到大排序为 3 cm , 6 cm , 9 cm , 18 cm , 故是成比例线段; D. 故不是成比例线段. C (1) 在判断是否成比例线段时,长度单位必须相同,若 长度单位不同,应先统一单位再判断; (2) 在判断是否成比例线段时,应首先将四条线段按长 短顺序排列起来,若两条较短线段的长度的比等于 两条较长的线段的比,则是成比例线段,否则不是. 方法总结 1. 四条线段 a 、 b 、 c 、 d 成比例,其中 b =3cm , c =2cm , d =6cm ,则 a = 2. 四个正数 a 、 b 、 c 、 d 能构成比例式,其中 b =3 , c =2 , d =6 ,则 a = . 3. 若 则 1 4 或 9 或 1 针对训练 4. 若线段 MN =10 ,点 K 为 MN 的黄金分割点,则 KM 的长为 . 考点二 平分线分线段成比例 例 2 如图,已知: △ABC 中, DE∥BC , AD=3 , DB=6 , AE=2 ,求 AC 的长. 解: ∵DE∥BC , ∴△ADE∽△ABC. ∴ 又 ∵AD=3 , DB=6 , AE=2 , ∴ 解得 EC=4 . ∴AC=AE+EC=6. 针对训练 5 .如图, AD∥BE∥CF ,直线 l 1 , l 2 与这三条平行线分别交于点 A , B , C 和点 D , E , F , , DE=6 ,则 EF= ___ . 6. 如图, DE∥BC , DF∥AC , AD = 4 cm , BD = 8 cm , DE = 5cm ,则线段 BF 的长为 _________cm . 9 10 例 3 如图, △ ABC 是等边三角形, CE 是外角平分线,点 D 在 AC 上,连结 BD 并延长与 CE 交于点 E . (1) 求证: △ ABD ∽△ CED ; (2) 若 AB =6 , AD =2 CD , 求 BE 的长 . 解:( 1 )∵△ ABC 是等边三角形, ∴∠ BAC =∠ ACB = 60° ,∠ ACF = 120° . ∵ CE 是外角平分线, ∴∠ ACE = 60° . ∴∠ BAC =∠ ACE . 又 ∵∠ ADB =∠ CDE ,∴△ ABD ∽△ CED . 考点三 相似三角形的 判定 和 性质 (2) 作 BM ⊥ AC 于点 M , AC = AB =6. ∴ AM = CM =3, ∵ AD = 2CD ,∴ CD = 2 , AD = 4 , MD = 1. 在 Rt△ BDM 中 , . 由 ( 1 )△ ABD ∽△ CED 得, M 7. 如图,在 △ ABC 中,已知 DE // BC , AD= 3 BD , S △ ABC =48 ,求 S △ ADE. A B C D E 3 1 解:∵ DE∥BC , ∴△ ADE ∽△ ABC. ∴ S △ ABC : S △ ADE = ∵ AD : BD = 1 : 3, ∴ AD : AB = 1 : 4. ∴ S △ ADE = 27. 针对训练 8. 如图,将矩形 ABCD 沿两条较长边的中点的连线对折,得到的矩形 ADFE 与矩形 ABCD 相似,确定矩形 ABCD 长与宽的比 . A B C D E F 解: 矩形 ADFE 与矩形 ABCD 相似 , 9. 如图,在长 8cm 、宽 6cm 的矩形中,截去一个矩形(图中阴影部分所示),使留下的矩形与原矩形相似,那么留下的矩形面积为多少? 8cm 6cm 由题意得 解:设留下矩形的面积为 x cm 2 , 解得 x =27 cm 2 . 答:留下矩形的面积为 27 cm 2 . 10. 如图,△ ABC 是一张锐角三角形的硬纸片. AD 是边 BC 上的高, BC =40 , AD =30 .从这张硬纸片剪下一个长 HG 是宽 HE 的 2 倍的矩形 EFGH .使它的一边 EF 在 BC 上,顶点 G , H 分别在 AC , AB 上. AD 与 HG 的交点为 M . ( 1 )求证: ; ( 2 )求这个矩形 EFGH 的周长. (1) 证明:∵矩形 EFGH , ∴ EF ∥ GH . ∴ D A B C E F M N G D A B C E F M N G 解: (2) 设矩形的宽 HE = x , 则 MD = HE = x ∵ AD = 30 , ∴ AM = 30 – x . ∵ HG = 2 HE , ∴ HG = 2 x . ∵ ∴ ∴ x = 12. ∴ HE = 12 , HG = 24. ∴ 矩形 EFGH 的周长 =2 ( HE + HG ) =2 ( 12+24 ) = 72 . 例 4 小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下: 如示意图,小明边移动边观察,发现站到点 E 处时,可以使 自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度 恰好相同.此时,测得小明落在墙上的影子高度 CD = 1.2 m , CE = 0.8 m , CA = 30 m (点 A 、 E 、 C 在同一直线上). 已知小明的身高 EF 是 1.7 m ,请你帮小明求出楼高 AB (结果精确到 0.1 m ). 考点四 相似三角形的实际应用 解:过点 D 作 DG ⊥ AB ,分别交 AB 、 EF 于点 G 、 H , 则 EH = AG = CD = 1.2 m , DH = CE = 0.8 m , DG = CA = 30 m . 因为 EF 和 AB 都垂直于地面,所以 EF∥AB , 所以 ∠ BGD =∠ FHD =90°,∠ GBD =∠ HFD , 所以 △ BDG ∽△ FDH . 所以 G H 由题意,知 FH = EF - EH = 1.7 - 1.2 = 0.5 ( m ). 解得 BG = 18.75 ( m ). ∴ AB = BG + AG = 18.75+1.2 = 19.95≈20.0 ( m ). ∴楼高 AB 约为 20.0 m . 11. 在比例尺为 1∶200 的地图上,测得 A , B 两地间的图上距离为 4.5 cm ,则 A , B 两地间的实际距离为 __________ m . 【 解析 】 设 A , B 两地间的实际距离为 x cm , 则 即 x =900 , 又 900 cm=9 m . 答案: 9 针对训练 9 12. 如图,王芳同学跳起来把一个排球打在离地 2m 远的地上,然后反弹碰到墙上,如果她跳起击球时的高度是 1.8m ,排球落地点离墙的距离是 6m ,假设球扬直沿直线运动,球能碰到墙面离地多高的地方? A B O C D 2m 6m 1.8m 解: ∠ABO=∠CDO=90° ∠AOB=∠COD ∴△AOB∽△COD ∴ CD=5.4m 答:球能碰到墙面离地 5.4m 高的地方. x y 2 4 6 8 2 4 6 8 -2 -4 -6 -8 -2 -4 -6 -8 O 9 10 11 12 -9 -10 -12 例 5 如图,△ ABC 三个顶点坐标分别为 A ( 2 ,- 2 ), B ( 4 ,- 5 ) , C ( 5 ,- 2 ),以原点 O 为位似中心,将这个三角形放大为原来的 2 倍. A B C 解: A ' ( , ), B ' ( , ), C ' ( , ), 4 - 4 - 10 8 - 4 10 A" ( , ), B" ( , ), C" ( , ). 4 - 4 - 8 10 - 10 4 A ' B ' C ' A" B" C" 考点五 位似图形 针对训练 13. 如图,在边长为 1 的小正方形组成的网 格中,建立平面直角坐标系,△ ABO 与 △ A ′ B ′ O ′ 是 以点 P 为位似中心的位似 图形,它们的顶点均在格 点 ( 网格线的交点 ) 上,则 点 P 的坐标为 ( ) A . (0 , 0) B . (0 , 1) C . ( - 3 , 2) D . (3 ,- 2) C 14 .如图,正方形 ABCD 和正方形 OEFG 中 , 点 A 和点 F 的坐标分别为 (3 , 2) , ( - 1 ,- 1) ,则两个正方形的位似中心的坐标是 _____ ____ __________ . (1 , 0) 或 ( - 5 ,- 2) O x 课堂小结 图形的相似 比例线段 相似三角形 相似多边形 位似 比例的基本性质 比例线段 平行线分线段成比例 判定 性质 应用查看更多