- 2021-11-10 发布 |
- 37.5 KB |
- 11页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级上册数学周周测第二十二章 二次函数周周测5(22-3) 人教版
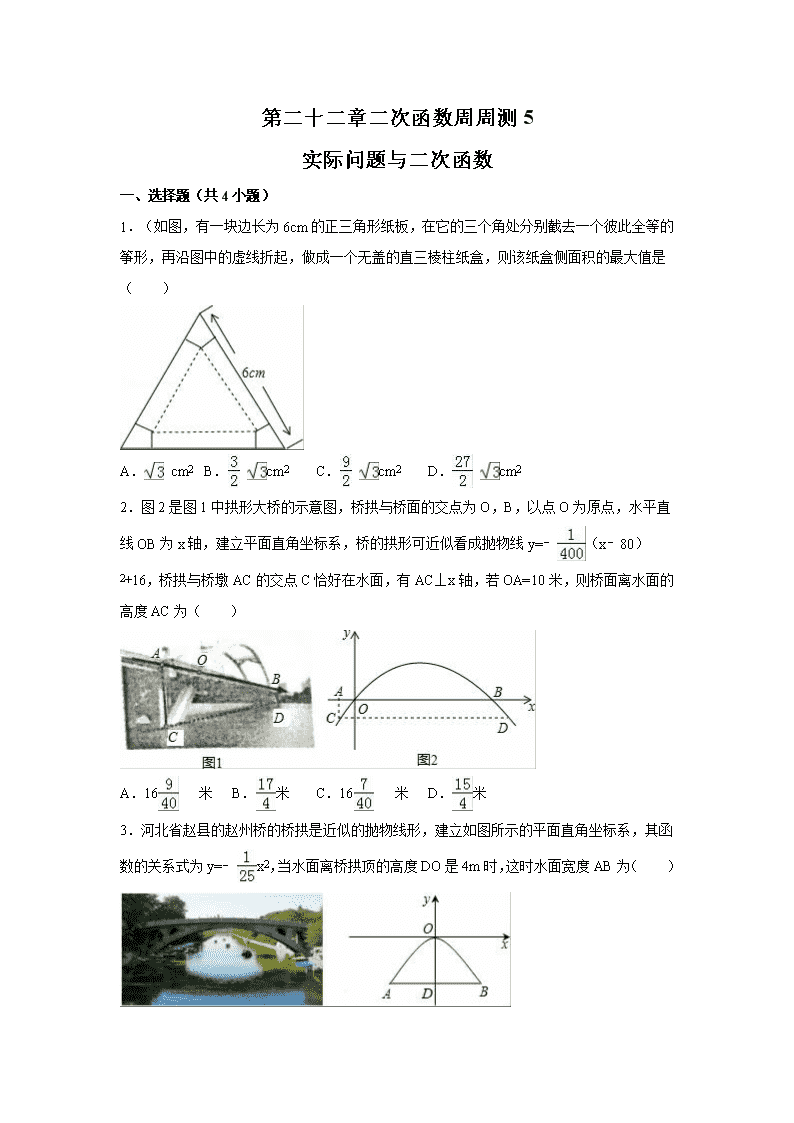
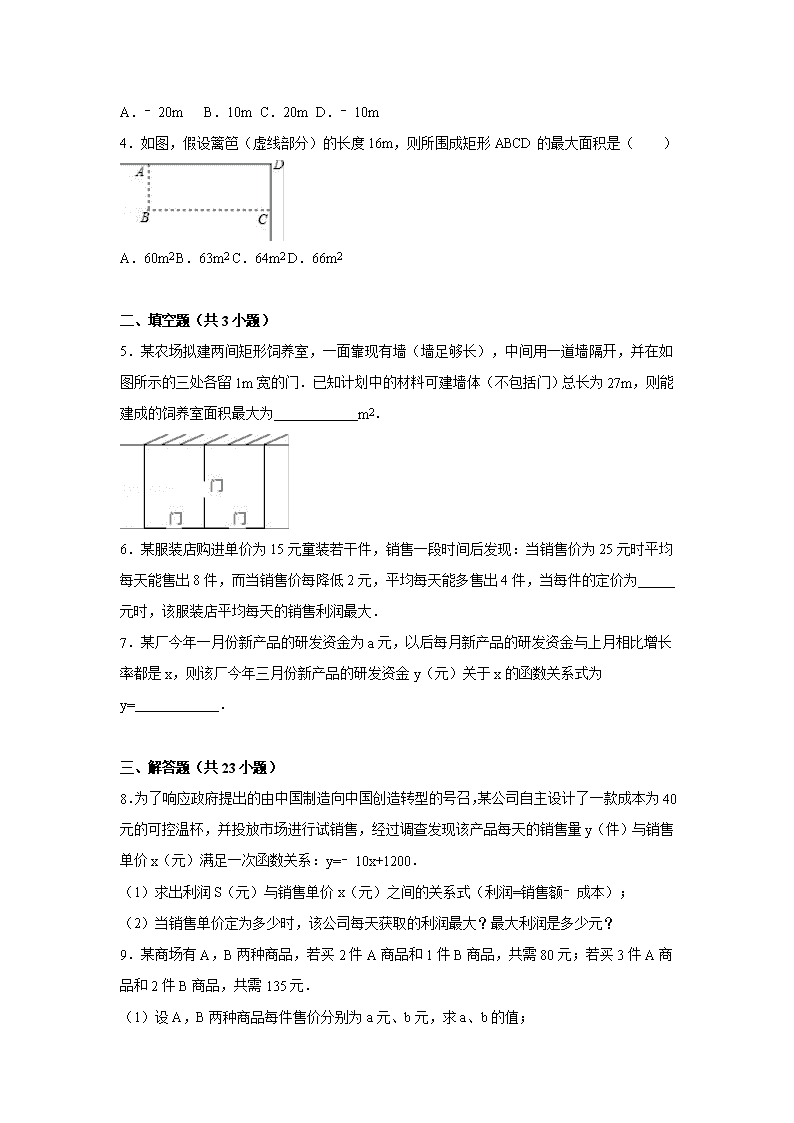
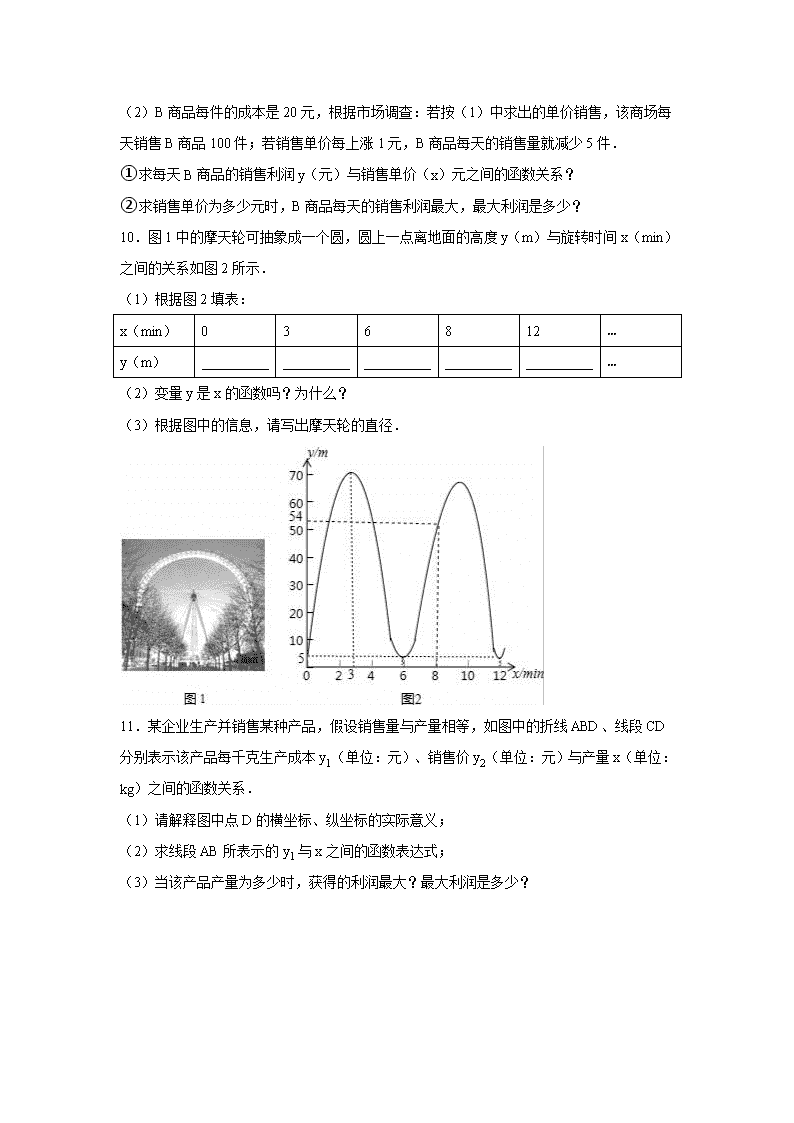
第二十二章二次函数周周测5 实际问题与二次函数 一、选择题(共4小题) 1.(如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( ) A. cm2 B. cm2 C. cm2 D. cm2 2.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣(x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( ) A.16米 B.米 C.16米 D.米 3.河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=﹣x2,当水面离桥拱顶的高度DO是4m时,这时水面宽度AB为( ) A.﹣20m B.10m C.20m D.﹣10m 4.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( ) A.60m2 B.63m2 C.64m2 D.66m2 二、填空题(共3小题) 5.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为 m2. 6.某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为 元时,该服装店平均每天的销售利润最大. 7.某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y= . 三、解答题(共23小题) 8.为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200. (1)求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本); (2)当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元? 9.某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元. (1)设A,B两种商品每件售价分别为a元、b元,求a、b的值; (2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件. ①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系? ②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少? 10.图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示. (1)根据图2填表: x(min) 0 3 6 8 12 … y(m) … (2)变量y是x的函数吗?为什么? (3)根据图中的信息,请写出摩天轮的直径. 11.某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系. (1)请解释图中点D的横坐标、纵坐标的实际意义; (2)求线段AB所表示的y1与x之间的函数表达式; (3)当该产品产量为多少时,获得的利润最大?最大利润是多少? 12.(2015•天水)天水“伏羲文化节”商品交易会上,某商人将每件进价为8元的纪念品,按每件9元出售,每天可售出20件.他想采用提高售价的办法来增加利润,经实验,发现这种纪念品每件提价1元,每天的销售量会减少4件. (1)写出每天所得的利润y(元)与售价x(元/件)之间的函数关系式. (2)每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元? 13.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2. (1)求y与x之间的函数关系式,并注明自变量x的取值范围; (2)x为何值时,y有最大值?最大值是多少? 14.某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表: x(件) … 5 10 15 20 … y(元/件) … 75 70 65 60 … (1)由题意知商品的最低销售单价是 元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围; (2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元? 15.某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下: x 30 32 34 36 y 40 36 32 28 (1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围); (2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元? (3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大? 16.某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元. (1)求y与x的函数关系式,并写出自变量x的取值范围; (2)顾客一次性购买多少件时,该网店从中获利最多? 17.如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为m. (1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离; (2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过? (3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米? 18.某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据: t(秒) 0 0.16 0.2 0.4 0.6 0.64 0.8 6 X(米) 0 0.4 0.5 1 1.5 1.6 2 … y(米) 0.25 0.378 0.4 0.45 0.4 0.378 0.25 … (1)当t为何值时,乒乓球达到最大高度? (2)乒乓球落在桌面时,与端点A的水平距离是多少? (3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k. ①用含a的代数式表示k; ②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求a的值. 19.如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m. (1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少? (2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门? 20.某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: y=. (1)李明第几天生产的粽子数量为420只? (2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本) (3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元? 21.某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息: ①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表: 时间(第x天) 1 3 6 10 … 日销售量(m件) 198 194 188 180 … ②该产品90天内每天的销售价格与时间(第x天)的关系如下表: 时间(第x天) 1≤x<50 50≤x≤90 销售价格(元/件) x+60 100 (1)求m关于x的一次函数表达式; (2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格﹣每件成本)】 (3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果. 22.某动车站在原有的普通售票窗口外新增了无人售票窗口,普通售票窗口从上午8点开放,而无人售票窗口从上午7点开放,某日从上午7点到10点,每个普通售票窗口售出的车票数y1(张)与售票时间x(小时)的变化趋势如图1,每个无人售票窗口售出的车票数y2(张)与售票时间x(小时)的变化趋势是以原点为顶点的抛物线的一部分,如图2,若该日截至上午9点,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同. (1)求图2中所确定抛物线的解析式; (2)若该日共开放5个无人售票窗口,截至上午10点,两种窗口共售出的车票数不少于900张,则至少需要开放多少个普通售票窗口? 23.某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y= (1)李明第几天生产的粽子数量为420只? (2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图形来刻画.若李明第x天创造的利润为w元,求w关于x的函数表达式,并求出第几天的利润最大,最大利润时多少元?(利润=出厂价﹣成本) 24.大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月饰品销量为y(件),月利润为w(元). (1)直接写出y与x之间的函数关系式; (2)如何确定销售价格才能使月利润最大?求最大月利润; (3)为了使每月利润不少于6000元应如何控制销售价格? 25.一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件,为提高利益,就对该T恤进行涨价销售,经过调查发现,每涨价1元,每周要少卖出10件,请确定该T恤涨价后每周销售利润y(元)与销售单价x(元)之间的函数关系式,并求出销售单价定为多少元时,每周的销售利润最大? 26.某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示. (1)求y关于x的函数关系式(不要求写出x的取值范围); (2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少? 27.为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒. (1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式; (2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少? (3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒? 28为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数. (1)求彩虹桥上车流密度为100辆/千米时的车流速度; (2)在交通高峰时段,为使彩虹桥上车流速度大于40千米/小时且小于60千米/小时,应控制彩虹桥上的车流密度在什么范围内? (3)当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20≤x≤220时,求彩虹桥上车流量y的最大值. 29.某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?下面是两位学生争议的情境: 请根据上面的信息,解决问题: (1)设AB=x米(x>0),试用含x的代数式表示BC的长; (2)请你判断谁的说法正确,为什么? 30.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表: 售价(元/件) 100 110 120 130 … 月销量(件) 200 180 160 140 … 已知该运动服的进价为每件60元,设售价为x元. (1)请用含x的式子表示:①销售该运动服每件的利润是 ( )元;②月销量是 ( )件;(直接写出结果) (2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少? 查看更多