2019年甘肃省中考数学试卷含答案

2019年甘肃省中考数学试卷含答案

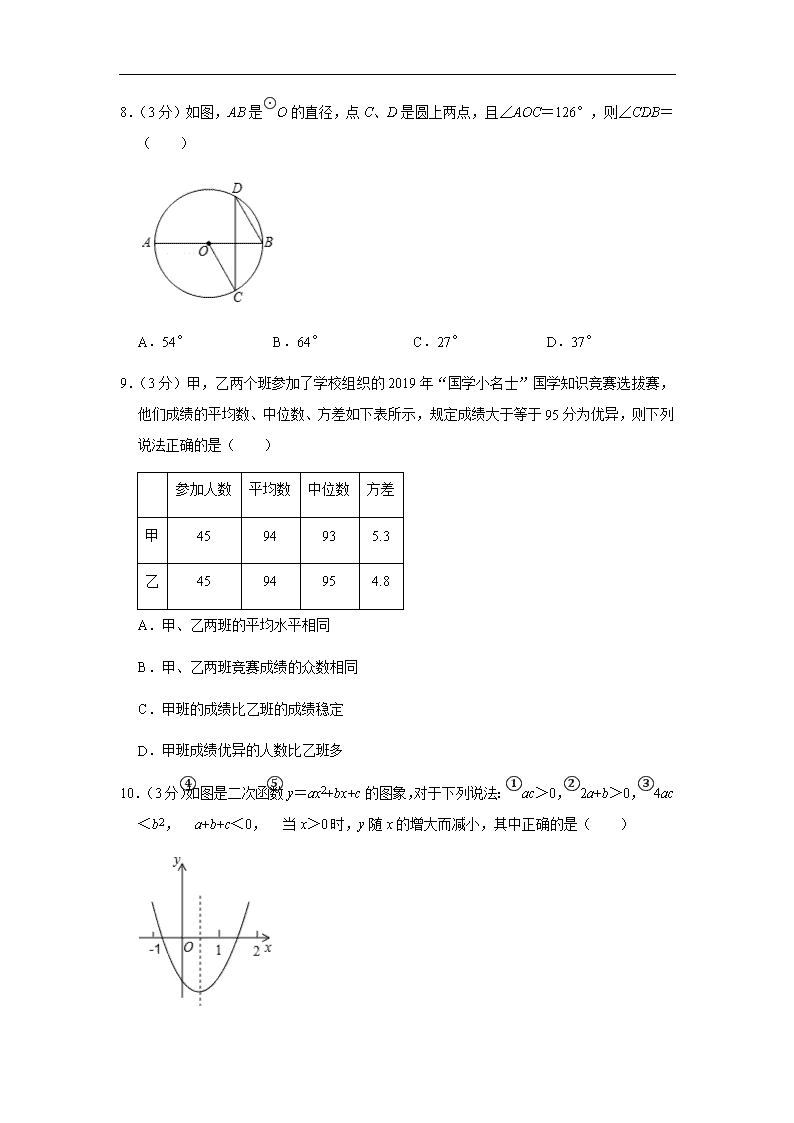
‎2019年甘肃省中考数学试卷 一、选择题：本大题共10小题，每小题3分，共30分，每小只有一个正确选项.‎ ‎1．（3分）下列四个图案中，是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎2．（3分）在0，2，﹣3，‎-‎‎1‎‎2‎这四个数中，最小的数是（　　）‎ A．0 B．2 C．﹣3 D．‎‎-‎‎1‎‎2‎ ‎3．（3分）使得式子x‎4-x有意义的x的取值范围是（　　）‎ A．x≥4 B．x＞4 C．x≤4 D．x＜4‎ ‎4．（3分）计算（﹣2a）2•a4的结果是（　　）‎ A．﹣4a6 B．4a6 C．﹣2a6 D．﹣4a8‎ ‎5．（3分）如图，将一块含有30°的直角三角板的顶点放在直尺的一边上，若∠1＝48°，那么∠2的度数是（　　）‎ A．48° B．78° C．92° D．102°‎ ‎6．（3分）已知点P（m+2，2m﹣4）在x轴上，则点P的坐标是（　　）‎ A．（4，0） B．（0，4） C．（﹣4，0） D．（0，﹣4）‎ ‎7．（3分）若一元二次方程x2﹣2kx+k2＝0的一根为x＝﹣1，则k的值为（　　）‎ A．﹣1 B．0 C．1或﹣1 D．2或0‎ ‎8．（3分）如图，AB是⊙O的直径，点C、D是圆上两点，且∠AOC＝126°，则∠CDB＝（　　）‎ A．54° B．64° C．27° D．37°‎ ‎9．（3分）甲，乙两个班参加了学校组织的2019年“国学小名士”国学知识竞赛选拔赛，他们成绩的平均数、中位数、方差如下表所示，规定成绩大于等于95分为优异，则下列说法正确的是（　　）‎ 参加人数 平均数 中位数 方差 甲 ‎45‎ ‎94‎ ‎93‎ ‎5.3‎ 乙 ‎45‎ ‎94‎ ‎95‎ ‎4.8‎ A．甲、乙两班的平均水平相同 ‎ B．甲、乙两班竞赛成绩的众数相同 ‎ C．甲班的成绩比乙班的成绩稳定 ‎ D．甲班成绩优异的人数比乙班多 ‎10．（3分）如图是二次函数y＝ax2+bx+c的图象，对于下列说法：①ac＞0，②2a+b＞0，③4ac＜b2，④a+b+c＜0，⑤当x＞0时，y随x的增大而减小，其中正确的是（　　）‎ A．①②③ B．①②④ C．②③④ D．③④⑤‎ 二、填空题：本大题共8小题，每小题3分，共24分.‎ ‎11．（3分）分解因式：x3y﹣4xy＝　 　．‎ ‎12．（3分）不等式组‎2-x≥0‎‎2x＞x-1‎的最小整数解是　 　．‎ ‎13．（3分）分式方程‎3‎x+1‎‎=‎‎5‎x+2‎的解为　 　．‎ ‎14．（3分）在△ABC中∠C＝90°，tanA‎=‎‎3‎‎3‎，则cosB＝　 　．‎ ‎15．（3分）已知某几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的左视图的面积为　 　．‎ ‎16．（3分）如图，在Rt△ABC中，∠C＝90°，AC＝BC＝2，点D是AB的中点，以A、B为圆心，AD、BD长为半径画弧，分别交AC、BC于点E、F，则图中阴影部分的面积为　 　．‎ ‎17．（3分）如图，在矩形ABCD中，AB＝10，AD＝6，E为BC上一点，把△CDE沿DE折叠，使点C落在AB边上的F处，则CE的长为　 　．‎ ‎18．（3分）如图，每一图中有若干个大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，如果第n幅图中有2019个菱形，则n＝　 　．‎ 三、解答题（一）本大共5小题，共26分.解答应写出必要的文字说明，证明过程成演算步骤.‎ ‎19．（4分）计算：（‎-‎‎1‎‎2‎）﹣2+（2019﹣π）0‎-‎‎3‎‎3‎tan60°﹣|﹣3|．‎ ‎20．（4分）如图，在△ABC中，点P是AC上一点，连接BP，求作一点M，使得点M到AB和AC两边的距离相等，并且到点B和点P的距离相等．（不写作法，保留作图痕迹）‎ ‎21．（6分）中国古代入民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题，原文：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？‎ ‎22．（6分）为了保证人们上下楼的安全，楼梯踏步的宽度和高度都要加以限制．中小学楼梯宽度的范围是260mm～300mm含（300mm），高度的范围是120mm～150mm（含150mm）．如图是某中学的楼梯扶手的截面示意图，测量结果如下：AB，CD分别垂直平分踏步EF，GH，各踏步互相平行，AB＝CD，AC＝900mm，∠ACD＝65°，试问该中学楼梯踏步的宽度和高度是否符合规定．（结果精确到1mm，参考数据：sin65°≈0.906，cos65°≈0.423）‎ ‎23．（6分）在甲乙两个不透明的口袋中，分别有大小、材质完全相同的小球，其中甲口袋中的小球上分别标有数字1，2，3，4，乙口袋中的小球上分别标有数字2，3，4，先从甲袋中任意摸出一个小球，记下数字为m，再从乙袋中摸出一个小球，记下数字为n．‎ ‎（1）请用列表或画树状图的方法表示出所有（m，n）可能的结果；‎ ‎（2）若m，n都是方程x2﹣5x+6＝0的解时，则小明获胜；若m，n都不是方程x2﹣5x+6＝0的解时，则小利获胜，问他们两人谁获胜的概率大？‎ 四、解答题（二）：本大题共5小题，共40分解答应写出必要的文字说明，证明过程或演算步骤 ‎24．（7分）良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用，荤菜中蛋白质、钙、磷及脂溶性维生素优于素食，而素食中不饱和脂肪酸、维生素和纤维素又优于荤食，只有荤食与素食适当搭配，才能强化初中生的身体素质．某校为了了解学生的体质健康状况，以便食堂为学生提供合理膳食，对本校七年级、八年级学生的体质健康状况进行了调查，过程如下：‎ 收集数据：‎ 从七、八年级两个年级中各抽取15名学生，进行了体质健康测试，测试成绩（百分制）如下：‎ 七年级：74 81 75 76 70 75 75 79 81 70 74 80 91 69 82‎ 八年级：81 94 83 77 83 80 81 70 81 73 78 82 80 70 50‎ 整理数据：‎ 年级 x＜60‎ ‎60≤x＜80‎ ‎80≤x＜90‎ ‎90≤x≤100‎ 七年级 ‎0‎ ‎10‎ ‎4‎ ‎1‎ 八年级 ‎1‎ ‎5‎ ‎8‎ ‎1‎ ‎（说明：90分及以上为优秀，80～90分（不含90分）为良好，60～80分（不含80分）为及格，60分以下为不及格）‎ 分析数据：‎ 年级 平均数 中位数 众数 七年级 ‎　 　‎ ‎75‎ ‎75‎ 八年级 ‎77.5‎ ‎80‎ ‎　 　‎ 得出结论：‎ ‎（1）根据上述数据，将表格补充完整；‎ ‎（2）可以推断出　 　年级学生的体质健康状况更好一些，并说明理由；‎ ‎（3）若七年级共有300名学生，请估计七年级体质健康成绩优秀的学生人数．‎ ‎25．（7分）如图，一次函数y＝kx+b的图象与反比例函数y‎=‎mx的图象相交于A（﹣1，n）、B（2，﹣1）两点，与y轴相交于点C．‎ ‎（1）求一次函数与反比例函数的解析式；‎ ‎（2）若点D与点C关于x轴对称，求△ABD的面积；‎ ‎（3）若M（x1，y1）、N（x2，y2）是反比例函数y‎=‎mx上的两点，当x1＜x2＜0时，比较y2与y1的大小关系．‎ ‎26．（8分）如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G．‎ ‎（1）证明：△ADG≌△DCE；‎ ‎（2）连接BF，证明：AB＝FB．‎ ‎27．（8分）如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC于点E．‎ ‎（1）求证：∠A＝∠ADE；‎ ‎（2）若AD＝8，DE＝5，求BC的长．‎ ‎28．（10分）如图，已知二次函数y＝x2+bx+c的图象与x轴交于点A（1，0）、B（3，0），与y轴交于点C．‎ ‎（1）求二次函数的解析式；‎ ‎（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标；‎ ‎（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线BC于点D，求四边形AEBD面积的最大值及此时点E的坐标．‎ ‎2019年甘肃省中考数学试卷 参考答案与试题解析 一、选择题：本大题共10小题，每小题3分，共30分，每小只有一个正确选项.‎ ‎1．（3分）下列四个图案中，是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎【解答】解：A．此图案是中心对称图形，符合题意；‎ B．此图案不是中心对称图形，不合题意；‎ C．此图案不是中心对称图形，不合题意；‎ D．此图案不是中心对称图形，不合题意；‎ 故选：A．‎ ‎2．（3分）在0，2，﹣3，‎-‎‎1‎‎2‎这四个数中，最小的数是（　　）‎ A．0 B．2 C．﹣3 D．‎‎-‎‎1‎‎2‎ ‎【解答】解：根据实数比较大小的方法，可得 ‎﹣3‎＜-‎1‎‎2‎＜‎0＜2，‎ 所以最小的数是﹣3．‎ 故选：C．‎ ‎3．（3分）使得式子x‎4-x有意义的x的取值范围是（　　）‎ A．x≥4 B．x＞4 C．x≤4 D．x＜4‎ ‎【解答】解：使得式子x‎4-x有意义，则：4﹣x＞0，‎ 解得：x＜4，‎ 即x的取值范围是：x＜4．‎ 故选：D．‎ ‎4．（3分）计算（﹣2a）2•a4的结果是（　　）‎ A．﹣4a6 B．4a6 C．﹣2a6 D．﹣4a8‎ ‎【解答】解：（﹣2a）2•a4＝4a2•a4＝4a6．‎ 故选：B．‎ ‎5．（3分）如图，将一块含有30°的直角三角板的顶点放在直尺的一边上，若∠1＝48°，那么∠2的度数是（　　）‎ A．48° B．78° C．92° D．102°‎ ‎【解答】解：∵将一块含有30°的直角三角板的顶点放在直尺的一边上，∠1＝48°，‎ ‎∴∠2＝∠3＝180°﹣48°﹣30°＝102°．‎ 故选：D．‎ ‎6．（3分）已知点P（m+2，2m﹣4）在x轴上，则点P的坐标是（　　）‎ A．（4，0） B．（0，4） C．（﹣4，0） D．（0，﹣4）‎ ‎【解答】解：∵点P（m+2，2m﹣4）在x轴上，‎ ‎∴2m﹣4＝0，‎ 解得：m＝2，‎ ‎∴m+2＝4，‎ 则点P的坐标是：（4，0）．‎ 故选：A．‎ ‎7．（3分）若一元二次方程x2﹣2kx+k2＝0的一根为x＝﹣1，则k的值为（　　）‎ A．﹣1 B．0 C．1或﹣1 D．2或0‎ ‎【解答】解：把x＝﹣1代入方程得：1+2k+k2＝0，‎ 解得：k＝﹣1，‎ 故选：A．‎ ‎8．（3分）如图，AB是⊙O的直径，点C、D是圆上两点，且∠AOC＝126°，则∠CDB＝（　　）‎ A．54° B．64° C．27° D．37°‎ ‎【解答】解：∵∠AOC＝126°，‎ ‎∴∠BOC＝180°﹣∠AOC＝54°，‎ ‎∵∠CDB‎=‎‎1‎‎2‎∠BOC＝27°．‎ 故选：C．‎ ‎9．（3分）甲，乙两个班参加了学校组织的2019年“国学小名士”国学知识竞赛选拔赛，他们成绩的平均数、中位数、方差如下表所示，规定成绩大于等于95分为优异，则下列说法正确的是（　　）‎ 参加人数 平均数 中位数 方差 甲 ‎45‎ ‎94‎ ‎93‎ ‎5.3‎ 乙 ‎45‎ ‎94‎ ‎95‎ ‎4.8‎ A．甲、乙两班的平均水平相同 ‎ B．甲、乙两班竞赛成绩的众数相同 ‎ C．甲班的成绩比乙班的成绩稳定 ‎ D．甲班成绩优异的人数比乙班多 ‎【解答】解：A、甲、乙两班的平均水平相同；正确；‎ B、甲、乙两班竞赛成绩的众数相同；不正确；‎ C、甲班的成绩比乙班的成绩稳定；不正确；‎ D、甲班成绩优异的人数比乙班多；不正确；‎ 故选：A．‎ ‎10．（3分）如图是二次函数y＝ax2+bx+c的图象，对于下列说法：①ac＞0，②2a+b＞0，③4ac＜b2，④a+b+c＜0，⑤当x＞0时，y随x的增大而减小，其中正确的是（　　）‎ A．①②③ B．①②④ C．②③④ D．③④⑤‎ ‎【解答】解：①由图象可知：a＞0，c＜0，‎ ‎∴ac＜0，故①错误；‎ ‎②由于对称轴可知：‎-b‎2a＜‎1，‎ ‎∴2a+b＞0，故②正确；‎ ‎③由于抛物线与x轴有两个交点，‎ ‎∴△＝b2﹣4ac＞0，故③正确；‎ ‎④由图象可知：x＝1时，y＝a+b+c＜0，‎ 故④正确；‎ ‎⑤当x‎＞-‎b‎2a时，y随着x的增大而增大，故⑤错误；‎ 故选：C．‎ 二、填空题：本大题共8小题，每小题3分，共24分.‎ ‎11．（3分）分解因式：x3y﹣4xy＝　xy（x+2）（x﹣2）　．‎ ‎【解答】解：x3y﹣4xy，‎ ‎＝xy（x2﹣4），‎ ‎＝xy（x+2）（x﹣2）．‎ ‎12．（3分）不等式组‎2-x≥0‎‎2x＞x-1‎的最小整数解是　0　．‎ ‎【解答】解：不等式组整理得：x≤2‎x＞-1‎，‎ ‎∴不等式组的解集为﹣1＜x≤2，‎ 则最小的整数解为0，‎ 故答案为：0‎ ‎13．（3分）分式方程‎3‎x+1‎‎=‎‎5‎x+2‎的解为　‎1‎‎2‎　．‎ ‎【解答】解：去分母得：3x+6＝5x+5，‎ 解得：x‎=‎‎1‎‎2‎，‎ 经检验x‎=‎‎1‎‎2‎是分式方程的解．‎ 故答案为：‎1‎‎2‎．‎ ‎14．（3分）在△ABC中∠C＝90°，tanA‎=‎‎3‎‎3‎，则cosB＝　‎1‎‎2‎　．‎ ‎【解答】解：利用三角函数的定义及勾股定理求解．‎ ‎∵在Rt△ABC中，∠C＝90°，tanA‎=‎‎3‎‎3‎，‎ 设a‎=‎‎3‎x，b＝3x，则c＝2‎3‎x，‎ ‎∴cosB‎=ac=‎‎1‎‎2‎．‎ 故答案为：‎1‎‎2‎．‎ ‎15．（3分）已知某几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的左视图的面积为　6cm2　．‎ ‎【解答】解：该几何体是一个三棱柱，底面等边三角形边长为2cm，三棱柱的高为3，所以，其左视图的面积为3×2＝6（cm2），‎ 故答案为6cm2．‎ ‎16．（3分）如图，在Rt△ABC中，∠C＝90°，AC＝BC＝2，点D是AB的中点，以A、B为圆心，AD、BD长为半径画弧，分别交AC、BC于点E、F，则图中阴影部分的面积为　2‎-‎π‎4‎　．‎ ‎【解答】解：在Rt△ABC中，∵∠ACB＝90°，CA＝CB＝2，‎ ‎∴AB＝2‎2‎，∠A＝∠B＝45°，‎ ‎∵D是AB的中点，‎ ‎∴AD＝DB‎=‎‎2‎，‎ ‎∴S阴＝S△ABC﹣2•S扇形ADE‎=‎1‎‎2‎×‎2×2﹣2‎×‎45⋅π⋅(‎‎2‎‎)‎‎2‎‎360‎=‎2‎-‎π‎4‎，‎ 故答案为：2‎‎-‎π‎4‎ ‎17．（3分）如图，在矩形ABCD中，AB＝10，AD＝6，E为BC上一点，把△CDE沿DE折叠，使点C落在AB边上的F处，则CE的长为　‎10‎‎3‎　．‎ ‎【解答】解：设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，‎ 在Rt△DAF中，AD＝6，DF＝10，‎ ‎∴AF＝8，‎ ‎∴BF＝AB﹣AF＝10﹣8＝2，‎ 在Rt△BEF中，BE2+BF2＝EF2，‎ 即（6﹣x）2+22＝x2，‎ 解得x‎=‎‎10‎‎3‎，‎ 故答案为‎10‎‎3‎．‎ ‎18．（3分）如图，每一图中有若干个大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，如果第n幅图中有2019个菱形，则n＝　1010　．‎ ‎【解答】解：根据题意分析可得：第1幅图中有1个．‎ 第2幅图中有2×2﹣1＝3个．‎ 第3幅图中有2×3﹣1＝5个．‎ 第4幅图中有2×4﹣1＝7个．‎ ‎…．‎ 可以发现，每个图形都比前一个图形多2个．‎ 故第n幅图中共有（2n﹣1）个．‎ 当图中有2019个菱形时，‎ ‎2n﹣1＝2019，‎ n＝1010，‎ 故答案为：1010．‎ 三、解答题（一）本大共5小题，共26分.解答应写出必要的文字说明，证明过程成演算步骤.‎ ‎19．（4分）计算：（‎-‎‎1‎‎2‎）﹣2+（2019﹣π）0‎-‎‎3‎‎3‎tan60°﹣|﹣3|．‎ ‎【解答】解：原式＝4+1‎-‎3‎‎3‎×‎3‎-3‎，‎ ‎＝1．‎ ‎20．（4分）如图，在△ABC中，点P是AC上一点，连接BP，求作一点M，使得点M到AB和AC两边的距离相等，并且到点B和点P的距离相等．（不写作法，保留作图痕迹）‎ ‎【解答】解：如图，点M即为所求，‎ ‎21．（6分）中国古代入民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题，原文：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？‎ ‎【解答】解：设共有x人，‎ 根据题意得：x‎3‎‎+‎2‎=‎x-9‎‎2‎，‎ 去分母得：2x+12＝3x﹣27，‎ 解得：x＝39，‎ ‎∴‎39-9‎‎2‎‎=‎15，‎ 则共有39人，15辆车．‎ ‎22．（6分）为了保证人们上下楼的安全，楼梯踏步的宽度和高度都要加以限制．中小学楼梯宽度的范围是260mm～300mm含（300mm），高度的范围是120mm～150mm（含150mm）．如图是某中学的楼梯扶手的截面示意图，测量结果如下：AB，CD分别垂直平分踏步EF，GH，各踏步互相平行，AB＝CD，AC＝900mm，∠ACD＝65°，试问该中学楼梯踏步的宽度和高度是否符合规定．（结果精确到1mm ‎，参考数据：sin65°≈0.906，cos65°≈0.423）‎ ‎【解答】解：连接BD，作DM⊥AB于点M，‎ ‎∵AB＝CD，AB，CD分别垂直平分踏步EF，GH，‎ ‎∴AB∥CD，AB＝CD，‎ ‎∴四边形ABCD是平行四边形，‎ ‎∴∠C＝∠ABD，AC＝BD，‎ ‎∵∠C＝65°，AC＝900，‎ ‎∴∠ABD＝65°，BD＝900，‎ ‎∴BM＝BD•cos65°＝900×0.423≈381，DM＝BD•sin65°＝900×0.906≈815，‎ ‎∵381÷3＝127，120＜127＜150，‎ ‎∴该中学楼梯踏步的高度符合规定，‎ ‎∵815÷3≈272，260＜272＜300，‎ ‎∴该中学楼梯踏步的宽度符合规定，‎ 由上可得，该中学楼梯踏步的宽度和高度都符合规定．‎ ‎23．（6分）在甲乙两个不透明的口袋中，分别有大小、材质完全相同的小球，其中甲口袋中的小球上分别标有数字1，2，3，4，乙口袋中的小球上分别标有数字2，3，4，先从甲袋中任意摸出一个小球，记下数字为m，再从乙袋中摸出一个小球，记下数字为n．‎ ‎（1）请用列表或画树状图的方法表示出所有（m，n）可能的结果；‎ ‎（2）若m，n都是方程x2﹣5x+6＝0的解时，则小明获胜；若m，n都不是方程x2﹣5x+6＝0的解时，则小利获胜，问他们两人谁获胜的概率大？‎ ‎【解答】解：（1）树状图如图所示：‎ ‎（2）∵m，n都是方程x2﹣5x+6＝0的解，‎ ‎∴m＝2，n＝3，或m＝3，n＝2，‎ 由树状图得：共有12个等可能的结果，m，n都是方程x2﹣5x+6＝0的解的结果有2个，‎ m，n都不是方程x2﹣5x+6＝0的解的结果有2个，‎ 小明获胜的概率为‎2‎‎12‎‎=‎‎1‎‎6‎，小利获胜的概率为‎2‎‎12‎‎=‎‎1‎‎6‎，‎ ‎∴小明、小利获胜的概率一样大．‎ 四、解答题（二）：本大题共5小题，共40分解答应写出必要的文字说明，证明过程或演算步骤 ‎24．（7分）良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用，荤菜中蛋白质、钙、磷及脂溶性维生素优于素食，而素食中不饱和脂肪酸、维生素和纤维素又优于荤食，只有荤食与素食适当搭配，才能强化初中生的身体素质．某校为了了解学生的体质健康状况，以便食堂为学生提供合理膳食，对本校七年级、八年级学生的体质健康状况进行了调查，过程如下：‎ 收集数据：‎ 从七、八年级两个年级中各抽取15名学生，进行了体质健康测试，测试成绩（百分制）如下：‎ 七年级：74 81 75 76 70 75 75 79 81 70 74 80 91 69 82‎ 八年级：81 94 83 77 83 80 81 70 81 73 78 82 80 70 50‎ 整理数据：‎ 年级 x＜60‎ ‎60≤x＜80‎ ‎80≤x＜90‎ ‎90≤x≤100‎ 七年级 ‎0‎ ‎10‎ ‎4‎ ‎1‎ 八年级 ‎1‎ ‎5‎ ‎8‎ ‎1‎ ‎（说明：90分及以上为优秀，80～90分（不含90分）为良好，60～80分（不含80分）为及格，60分以下为不及格）‎ 分析数据：‎ 年级 平均数 中位数 众数 七年级 ‎　76.8　‎ ‎75‎ ‎75‎ 八年级 ‎77.5‎ ‎80‎ ‎　81　‎ 得出结论：‎ ‎（1）根据上述数据，将表格补充完整；‎ ‎（2）可以推断出　八　年级学生的体质健康状况更好一些，并说明理由；‎ ‎（3）若七年级共有300名学生，请估计七年级体质健康成绩优秀的学生人数．‎ ‎【解答】解：（1）七年级的平均数为‎1‎‎15‎（74+81+75+76+70+75+75+79+81+70+74+80+91+69+82）＝76.8，‎ 八年级的众数为81；‎ 故答案为：76.8；81；‎ ‎（2）八年级学生的体质健康状况更好一些；理由如下：‎ 八年级学生的平均数、中位数以及众数均高于七年级，说明八年级学生的体质健康情况更好一些；‎ 故答案为：八；‎ ‎（3）若七年级共有300名学生，则七年级体质健康成绩优秀的学生人数＝300‎×‎1‎‎15‎=‎20（人）．‎ ‎25．（7分）如图，一次函数y＝kx+b的图象与反比例函数y‎=‎mx的图象相交于A（﹣1，n）、B（2，﹣1）两点，与y轴相交于点C．‎ ‎（1）求一次函数与反比例函数的解析式；‎ ‎（2）若点D与点C关于x轴对称，求△ABD的面积；‎ ‎（3）若M（x1，y1）、N（x2，y2）是反比例函数y‎=‎mx上的两点，当x1＜x2＜0时，比较y2与y1的大小关系．‎ ‎【解答】解：（1）∵反比例函数y‎=‎mx经过点B（2，﹣1），‎ ‎∴m＝﹣2，‎ ‎∵点A（﹣1，n）在y‎=‎‎-2‎x上，‎ ‎∴n＝2，‎ ‎∴A（﹣1，2），‎ 把A，B坐标代入y＝kx+b，则有‎-k+b=2‎‎2k+b=-1‎，‎ 解得k=-1‎b=1‎，‎ ‎∴一次函数的解析式为y＝﹣x+1，反比例函数的解析式为y‎=-‎‎2‎x．‎ ‎（2）∵直线y＝﹣x+1交y轴于C，‎ ‎∴C（0，1），‎ ‎∵D，C关于x轴对称，‎ ‎∴D（0，﹣1），∵B（2，﹣1）‎ ‎∴BD∥x轴，‎ ‎∴S△ABD‎=‎1‎‎2‎×‎2×3＝3．‎ ‎（3）∵M（x1，y1）、N（x2，y2）是反比例函数y‎=-‎‎2‎x上的两点，且x1＜x2＜0，‎ ‎∴y1＜y2．‎ ‎26．（8分）如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G．‎ ‎（1）证明：△ADG≌△DCE；‎ ‎（2）连接BF，证明：AB＝FB．‎ ‎【解答】解：（1）∵四边形ABCD是正方形，‎ ‎∴∠ADG＝∠C＝90°，AD＝DC，‎ 又∵AG⊥DE，‎ ‎∴∠DAG+∠ADF＝90°＝∠CDE+∠ADF，‎ ‎∴∠DAG＝∠CDE，‎ ‎∴△ADG≌△DCE（ASA）；‎ ‎（2）如图所示，延长DE交AB的延长线于H，‎ ‎∵E是BC的中点，‎ ‎∴BE＝CE，‎ 又∵∠C＝∠HBE＝90°，∠DEC＝∠HEB，‎ ‎∴△DCE≌△HBE（ASA），‎ ‎∴BH＝DC＝AB，‎ 即B是AH的中点，‎ 又∵∠AFH＝90°，‎ ‎∴Rt△AFH中，BF‎=‎‎1‎‎2‎AH＝AB．‎ ‎27．（8分）如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC于点E．‎ ‎（1）求证：∠A＝∠ADE；‎ ‎（2）若AD＝8，DE＝5，求BC的长．‎ ‎【解答】（1）证明：连接OD，‎ ‎∵DE是切线，‎ ‎∴∠ODE＝90°，‎ ‎∴∠ADE+∠BDO＝90°，‎ ‎∵∠ACB＝90°，‎ ‎∴∠A+∠B＝90°，‎ ‎∵OD＝OB，‎ ‎∴∠B＝∠BDO，‎ ‎∴∠ADE＝∠A．‎ ‎（2）解：连接CD．‎ ‎∵∠ADE＝∠A，‎ ‎∴AE＝DE，‎ ‎∵BC是⊙O的直径，∠ACB＝90°，‎ ‎∴EC是⊙O的切线，‎ ‎∴ED＝EC，‎ ‎∴AE＝EC，‎ ‎∵DE＝5，‎ ‎∴AC＝2DE＝10，‎ 在Rt△ADC中，DC＝6，‎ 设BD＝x，在Rt△BDC中，BC2＝x2+62，在Rt△ABC中，BC2＝（x+8）2﹣102，‎ ‎∴x2+62＝（x+8）2﹣102，‎ 解得x‎=‎‎9‎‎2‎，‎ ‎∴BC‎=‎6‎‎2‎‎+(‎‎9‎‎2‎‎)‎‎2‎=‎‎15‎‎2‎．‎ ‎28．（10分）如图，已知二次函数y＝x2+bx+c的图象与x轴交于点A（1，0）、B（3，0），与y轴交于点C．‎ ‎（1）求二次函数的解析式；‎ ‎（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标；‎ ‎（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线BC于点D，求四边形AEBD面积的最大值及此时点E的坐标．‎ ‎【解答】解：（1）用交点式函数表达式得：y＝（x﹣1）（x﹣3）＝x2﹣4x+3；‎ 故二次函数表达式为：y＝x2﹣4x+3；‎ ‎（2）①当AB为平行四边形一条边时，如图1，‎ 则AB＝PE＝2，‎ 则点P坐标为（4，3），‎ 当点P在对称轴左侧时，即点C的位置，点A、B、P、F为顶点的四边形为平行四边形，‎ 故：点P（4，3）或（0，3）；‎ ‎②当AB是四边形的对角线时，如图2，‎ AB中点坐标为（2，0）‎ 设点P的横坐标为m，点F的横坐标为2，其中点坐标为：m+2‎‎2‎，‎ 即：m+2‎‎2‎‎=‎2，解得：m＝2，‎ 故点P（2，﹣1）；‎ 故：点P（4，3）或（0，3）或（2，﹣1）；‎ ‎（3）直线BC的表达式为：y＝﹣x+3，‎ 设点E坐标为（x，x2﹣4x+3），则点D（x，﹣x+3），‎ S四边形AEBD‎=‎‎1‎‎2‎AB（yD﹣yE）＝﹣x+3﹣x2+4x﹣3＝﹣x2+3x，‎ ‎∵﹣1＜0，故四边形AEBD面积有最大值，‎ 当x‎=‎‎3‎‎2‎，其最大值为‎9‎‎4‎，此时点E（‎3‎‎2‎，‎-‎‎3‎‎4‎）．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:56:28；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎