华东师大版九年级数学上册 第25章 随机事件的概率 单元检测试题（有答案）

华东师大版九年级数学上册 第25章 随机事件的概率 单元检测试题（有答案）

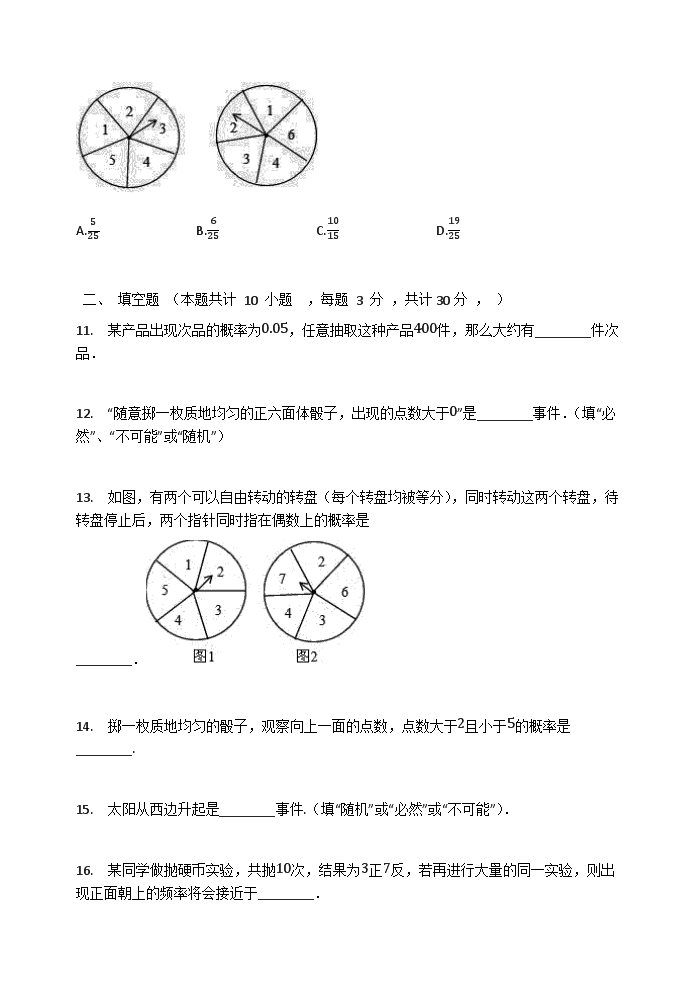
第 25 章 随机事件的概率 单元检测试题 （满分 120 分；时间：120 分钟） 一、 选择题 （本题共计 10 小题 ，每题 3 分 ，共计 30 分 ， ） 1. 下列说法正确的是（ ） A.哥哥的身高比弟弟高是必然事件 B.今年中秋节有雨是不确定事件 C.随机抛一枚均匀的硬币两次，都是正面朝上是不可能事件 D.“彩票中奖的概率为 ”表示买 张彩票肯定会中奖 2. 下列说法正确的是（ ） A.“抛一枚硬币正面朝上的概率是 概 ”表示每抛硬币 次就有 次出现正面朝上 B.一次抽奖活动中，“中奖的概率是 ”表示抽奖 次就一定会中奖 C.“明天降雨的概率是 ㌠㐶 ”表示明天有 ㌠㐶 的时间降雨 D.“刘明夺冠的可能性是 㐶 ”表示刘明夺冠的可能性很大 3. 下列诗句所描述的事件中，是不可能事件的是（ ） A.黄河入海流 B.锄禾日当午 C.大漠孤烟直 D.手可摘星辰 4. 小张、小王、小李三位同学随机地站成一排照相，小张恰好站在中间的概率是 A. ㌠ B. C. D. 5. 下列事件中是确定事件的为( ) A.两条线段可以组成一个三角形 B.打开电视机正在播放动画片 C.车辆随机经过一个路口，遇到绿灯 D.掷一枚均匀的骰子，掷出的点数是奇数 6. 某人把 粒黄豆染色后与一袋黄豆充分混匀，接着抓出 黄豆，数出其中有 粒黄豆被染色，则这袋黄豆原来有（ ） A. 粒 B. ㌠ 粒 C. 粒 D. 粒 7. 在不透明的袋子里装有 ㌠ 个红球和若干个白球，这些球除颜色不同外无其他差别.每 次从袋子里摸出一个球，记录下颜色后再放回，经过多次重复试验，发现摸到白球的频率 稳定在 概㌠ 左右，则袋中白球有( ) A. 个 B. 个 C. 个 D. 个 8. 下列说法正确的是（ ） A.“打开电视任选一频道，播放动画片”是必然事件 B.“任意画出一个正六边形，它的中心角是 ㌠ ”是必然事件 C.“旋转前、后的图形全等”是随机事件 D.任意掷一枚质地均匀的硬币 次正面朝上的一定是 次 9. 下面关于投针实验的说法正确的是（ ） A.针与平行线相交和不相交的可能性是相同的 B.针与平行线相交的概率与针的长度没有关系 C.实验次数越多，估算针与平行线相交的概率越精确 D.针与平行线相交的概率受两平行线间距离的影响 10. 如图所示的两个圆盘中，指针落在每一个数上的机会均等，则两个指针同时落在偶数 上的概率是（ ） A. B. ㌠ C. D. 二、 填空题 （本题共计 10 小题 ，每题 3 分 ，共计 30 分 ， ） 11. 某产品出现次品的概率为 概 ，任意抽取这种产品 件，那么大约有________件 次品． 12. “随意掷一枚质地均匀的正六面体骰子，出现的点数大于 ”是________事件．（填“必 然”、“不可能”或“随机”） 13. 如图，有两个可以自由转动的转盘（每个转盘均被等分），同时转动这两个转盘，待 转盘停止后，两个指针同时指在偶数上的概率是 ________． 14. 掷一枚质地均匀的骰子，观察向上一面的点数，点数大于 且小于 的概率是 ________. 15. 太阳从西边升起是________事件.（填“随机”或“必然”或“不可能”）． 16. 某同学做抛硬币实验，共抛 次，结果为 正 反，若再进行大量的同一实验，则 出现正面朝上的频率将会接近于________． 17. 下列事件： ①随意翻到一本书的某页，这页的页码是奇数；②测得某天的最高气温是 ； ③掷一次骰子，向上一面的数字是 ；④度量四边形的内角和，结果是 ㌠ ． 其中是随机事件的是________．（填序号） 18. 给出以下结论： ①如果一件事发生的机会只有十万分之一，那么它就不可能发生； ②二战时期美国某公司生产的降落伞合格率达 概㐶 ，使用该公司的降落伞不会发生危险； ③如果一件事不是必然发生的，那么它就不可能发生； ④从 、 、 、 、 中任取一个数是奇数的可能性要大于偶数的可能性． 其中不正确的结论是________． 19. 在元宵节这天，妈妈给乐乐盛了 ㌠ 个元宵(假设元宵的大小、形状完全相同），其中有 个是芝麻馅的，乐乐随机吃了 个，则这 个元宵都是芝麻馅的概率是_________． 20. 下列事件：①拔苗助长；②检验员从被检查的产品中抽取一件，就是合格品；③度 量五边形的内角和，结果是 ；④十拿九稳；⑤掷一枚骰子，向上一面的数字是 ．其 中是必然事件的有________，是随机事件的有________．（填序号） 三、 解答题 （本题共计 6 小题 ，共计 60 分 ， ） 21. 一个不透明的袋中放进若干个白球，现在想要知道这些白球的数目，小明用了如下的 方法：将 个与袋中白球大小、质量相同均相同的红球放入袋中，将红球与袋中的白球 充分搅匀后，再从袋中随机摸球，每次共摸 个球放回，共摸 次，求出红球与 的 比值，然后计算出平均值，得到摸到红球的概率是 㐶 ，求原来袋中约有多少个白球． 22. 国家主席习近平在二 二 年新年贺词中说：“垃圾分类引领着低碳生活新时尚”．“垃 圾分类”能有效节约原生资源，改善环境质量，带动绿色发展，引领绿色生活．为落实“垃 圾分类”，环卫部门要求要按 ， ， 三类分别装袋、投放，其中 类指废电池，过期药 品等有毒垃圾，甲投放了一袋垃圾，乙投放了两袋垃圾，这两袋垃圾不同类. 直接写出甲投放的垃圾恰好是 类的概率； 求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率. 23. 水果种植大户小芳组织了“草莓采摘游”活动，为了吸引更多的顾客，每一位来采摘草 莓的顾客都有一次抽奖机会.现有一只不透明的盒子，盒子里有三个外形与质地完全相同的 球，分别印有 (草莓)， (枇杷)， (葡萄). 抽奖活动 ：若顾客从盒子中任意摸一个球，摸到草莓就获得一张 元的优惠券，请 问顾客获得 元的优惠券的概率； 抽奖活动 ：若顾客从盒子中任意摸一个球后放回盒子，摇匀后再摸一个，两次摸到的 球都是草莓就可获得一张 元的优惠券，请列出顾客摸到球的所有可能情况，并求出获 得 元的优惠券的概率是多少？ 24. 某市正积极申报文明城市，周末市团委组织志愿者进行宣传活动 概 老师要从 名学生会 干部（小聪、小明、小可、小爱）中抽签选出 人去参加 概 抽签规则：将分别写有 人名字 的卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张，记下名字，再从剩余的 张 卡片中再随机抽取一张，记下名字 概 另一名学生会干部“小杰被抽中”是________事件，“小聪被抽中”是________事件（填“不 可能”或“必然”或“随机”）；第一次抽取卡片“小明被抽中”的概率为________. 用画树状图或列表的方法表示所有可能的结果，并求“小可和小爱一起被选中”的概率. 25. 手机微信推出了红包游戏，它有多种玩法，其中一种为“拼手气红包”，用户设好总金 额以及红包个数后，可以生成不等金额的红包，现有一用户发了三个“拼手气红包”，总金 额为 元，随机被甲、乙、丙三人抢到． 下列事件中，确定事件是________， ①丙抢到金额为 元的红包； ②乙抢到金额为 元的红包； ③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多； 记金额最多、居中、最少的红包分别为 ， ， ．求甲抢到红包 ，乙抢到红包 的 概率． 26. 端午节吃粽子是中华民族的传统习俗．又快到农历五月初五端午节了，小明奶奶包了 ㌠ 个粽子，其中有 个是枣豆馅的，有 个是鲜肉馅的，有 个是咸蛋黄馅的（这些粽子 除馅料不同外其他外观均相同．小明随手拿了两只来吃． （1）求小明第一个就吃到了喜欢的鲜肉馅粽子的概率． （2）求小明所吃两只粽子馅料相同的概率． （3）若在吃粽子之前，小明准备用一枚均匀的正六面体骰子进行吃粽子的模拟试验，规 定：掷得点数 ， ， 向上代表吃枣豆馅的，点数 ， 向上代表吃鲜肉馅的，点数 ㌠ 向 上代表吃咸蛋黄馅的，连续抛掷这个骰子两次表示随机吃两只粽子，从而估计吃两只粽子 刚好都是枣豆馅的概率．你认为这样模拟正确吗？试说明理由． 参考答案 一、 选择题 （本题共计 10 小题 ，每题 3 分 ，共计 30 分 ） 1. 【答案】 B 【解答】 解： 、哥哥的身高比弟弟高是随机事件，故 错误； 、今年中秋节有雨是不确定事件，故 正确； 、随机抛一枚均匀的硬币两次，都是正面朝上是随机事件，故 错误； 、“彩票中奖的概率为 ”表示买 张彩票可能中奖，可能不中奖，故 错误； 故选： ． 2. 【答案】 D 【解答】 解： 、“抛一枚硬币正面朝上的概率是 概 ”表示每抛硬币 次就有可能 次出现正面朝上， 也有可能两次正面朝上，也有可能两正面朝下，故 错误； 、一次抽奖活动中，“中奖的概率是 ”表示抽奖 次有可能中奖，也有可能不中奖， 故 错误； 、“明天降雨的概率是 ㌠㐶 ”表示明天降雨的可能性大，故 错误； 、“刘明夺冠的可能性是 㐶 ”表示刘明夺冠的可能性很大，故 正确； 故选： ． 3. 【答案】 D 【解答】 解： ，是必然事件，故选项错误； ，是随机事件，故选项错误； ，是随机事件，故选项错误； ，是不可能事件，故选项正确． 故选 ． 4. 【答案】 C 【解答】 解：小张、小王、小李三位同学随机地站成一排照相，有以下可能： 李张王，李王张，张李王，张王李，王李张，王张李， 共 ㌠ 种情况. 其中小张恰好站在中间有 种情况， 所以小张站在中间的概率是 ㌠ ． 故选 ． 5. 【答案】 A 【解答】 解： 、两条线段可以组成一个三角形是不可能事件，也是确定事件，故本选项正确； 、打开电视机正在播放动画片是随机事件，故本选项错误； 、车辆随机经过一个路口，遇到绿灯是随机事件，故本选项错误； 、掷一枚均匀的骰子，掷出的点数是奇数是随机事件，故本选项错误． 故选 ． 6. 【答案】 C 【解答】 设原黄豆数为 ，则 染色黄豆的概率为 h 解得 ＝ ． 7. 【答案】 C 【解答】 解：设袋中白球有 个，根据题意得： ㌠h 概㌠ ， 解得： ， 经检验： 是分式方程的解， 故袋中白球有 个. 故选 . 8. 【答案】 B 【解答】 解： 、“打开电视任选一频道，播放动画片”是随机事件，选项错误； 、“任意画出一个正六边形，它的中心角是 ㌠ ”是必然事件，选项正确； 、“旋转前、后的图形全等”是必然事件，选项错误； 、任意掷一枚质地均匀的硬币 次正面朝上的可能是 次，选项错误． 故选 ． 9. 【答案】 C 【解答】 解：实验次数越多，估算针与平行线相交的概率越精确，故选 ． 10. 【答案】 B 【解答】 解：画树状图为： 共有 种等可能的结果数，其中两个指针同时落在偶数上占 ㌠ 种， 所以两个指针同时落在偶数上的概率 ㌠ ． 故选 ． 二、 填空题 （本题共计 10 小题 ，每题 3 分 ，共计 30 分 ） 11. 【答案】 【解答】 解：由题意可得：次品数量 概 ． 故答案为： ． 12. 【答案】 必然 【解答】 解：因为正六面体骰子的数字为 ， ， ， ， ， ㌠ ， 所有数都大于 ， 所以出现点数都大于 是必然事件. 故答案为：必然. 13. 【答案】 ㌠ 【解答】 解：画树状图得： ∵ 共有 种等可能的结果，两个指针同时指在偶数上的有 ㌠ 种情况， ∴ 两个指针同时指在偶数上的概率是： ㌠ ， 故答案为： ㌠ ． 14. 【答案】 【解答】 解：掷一次骰子，向上一面的点数有 ㌠ 种情况， 其中有 种为点数大于 且小于 ， 故其概率是 ㌠ ． 故答案为： ． 15. 【答案】 不可能 【解答】 解：太阳从西边升起是不可能事件. 故答案为：不可能. 16. 【答案】 概 【解答】 解：抛硬币正面朝上的概率为 ，故进行大量的同一实验，则出现正面朝上的频率将会接 近于 概 ． 17. 【答案】 ①③ 【解答】 解：①是随机事件； ②是不可能事件； ③是随机事件； ④是必然事件． 故答案为：①③． 18. 【答案】 ①②③ 【解答】 解：①如果一件事发生的机会只有十万分之一，那么它就不可能发生，错误此事件有可能 发生，符合题意； ②二战时期美国某公司生产的降落伞合格率达 概㐶 ，使用该公司的降落伞不会发生危险， 错误，存在危险，符合题意； ③如果一件事不是必然发生的，那么它就不可能发生，错误，随机事件也可能发生，符合 题意； ④从 、 、 、 、 中任取一个数是奇数的可能性要大于偶数的可能性，正确，不合题 意． 故答案为：①②③． 19. 【答案】 【解答】 解：将 个芝麻馅的元宵均用 表示，另外 个元宵分别用 ， ， 表示，列表如下： 第一个 第二个 ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， 由表格可知，共有 种等可能的结果，其中 个都是芝麻馅的结果有 ㌠ 种，故所求概率 ㌠ ． 故答案为： ． 20. 【答案】 ①③,②④⑤ 【解答】 略 三、 解答题 （本题共计 6 小题 ，每题 10 分 ，共计 60 分 ） 21. 【答案】 袋子中原来有白球 个． 【解答】 解：设袋子中有 个白球，根据题意得： h 㐶 ， 解得： ． 22. 【答案】 解： 有 类垃圾，则甲投放的垃圾恰好是 类的概率为 . 共有 种等可能的结果，其中乙投放的垃圾恰有一袋与甲投放的垃圾是同类的结果数为 ， 所以乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率 概【解答】 解： 有 类垃圾，则甲投放的垃圾恰好是 类的概率为 . 共有 种等可能的结果，其中乙投放的垃圾恰有一袋与甲投放的垃圾是同类的结果数为 ， 所以乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率 概23. 【答案】 解： 由题意得，从盒子中任意摸出一个球，可能是草莓或枇杷或葡萄， 共 种可能，摸到草莓获得 元优惠券， 所以顾客获得 元的优惠券的概率是 ； 根据题意，顾客摸到球的所有可能情况如下表： 故获得 元的优惠券的概率 . 【解答】 解： 由题意得，从盒子中任意摸出一个球，可能是草莓或枇杷或葡萄， 共 种可能，摸到草莓获得 元优惠券， 所以顾客获得 元的优惠券的概率是 ； 根据题意，顾客摸到球的所有可能情况如下表： 故获得 元的优惠券的概率 . 24. 【答案】 不可能,随机, 树状图如图所示： 共有 种结果，其中“小可和小爱一起被选中”有 种：（可，爱），（爱，可）, ∴ 小可和小爱一起被选中 ㌠ . 【解答】 解： 名学生干部分别为小聪、小明、小可、小爱，小杰不在这 名学生干部中，故“小 杰被抽中”为不可能事件； 小聪、小明、小可、小爱这 人被抽中的概率是随机的，故“小聪被抽中”是随机事件； 小明被抽中 . 故答案为：不可能；随机； . 树状图如图所示： 共有 种结果，其中“小可和小爱一起被选中”有 种：（可，爱），（爱，可）, ∴ 小可和小爱一起被选中 ㌠ . 25. 【答案】 ② 由树状图可得出： 因为有 ， ， 三个红包，且抢到每一个红包的可能性相同， 共有 ㌠ 种情况，恰好甲抢到红包 ，乙抢到红包 有 种情况，所以概率为 ㌠ ． 【解答】 解： 事件①，③是不确定事件，事件②是不可能事件，即为确定事件. 故答案为：②. 由树状图可得出： 因为有 ， ， 三个红包，且抢到每一个红包的可能性相同， 共有 ㌠ 种情况，恰好甲抢到红包 ，乙抢到红包 有 种情况，所以概率为 ㌠ ． 26. 【答案】 解：（1）小明第一个就吃到了喜欢的鲜肉馅粽子的概率是 ㌠ ． （2）设枣豆馅的、鲜肉馅的、咸蛋黄馅的分别为 、 、 ，列表得： - - - - - - ∴ 一共有 种情况，小明所吃两只粽子馅料相同的有 种情况， ∴ 小明所吃两只粽子馅料相同的概率是 ． （3）不正确．概率问题需要做多次试验，才可近似求得． 【解答】 解：（1）小明第一个就吃到了喜欢的鲜肉馅粽子的概率是 ㌠ ． （2）设枣豆馅的、鲜肉馅的、咸蛋黄馅的分别为 、 、 ，列表得： - - - - - - ∴ 一共有 种情况，小明所吃两只粽子馅料相同的有 种情况， ∴ 小明所吃两只粽子馅料相同的概率是 ． （3）不正确．概率问题需要做多次试验，才可近似求得．