2020年秋九年级数学上册 第4章解直角三角形的应用

2020年秋九年级数学上册 第4章解直角三角形的应用

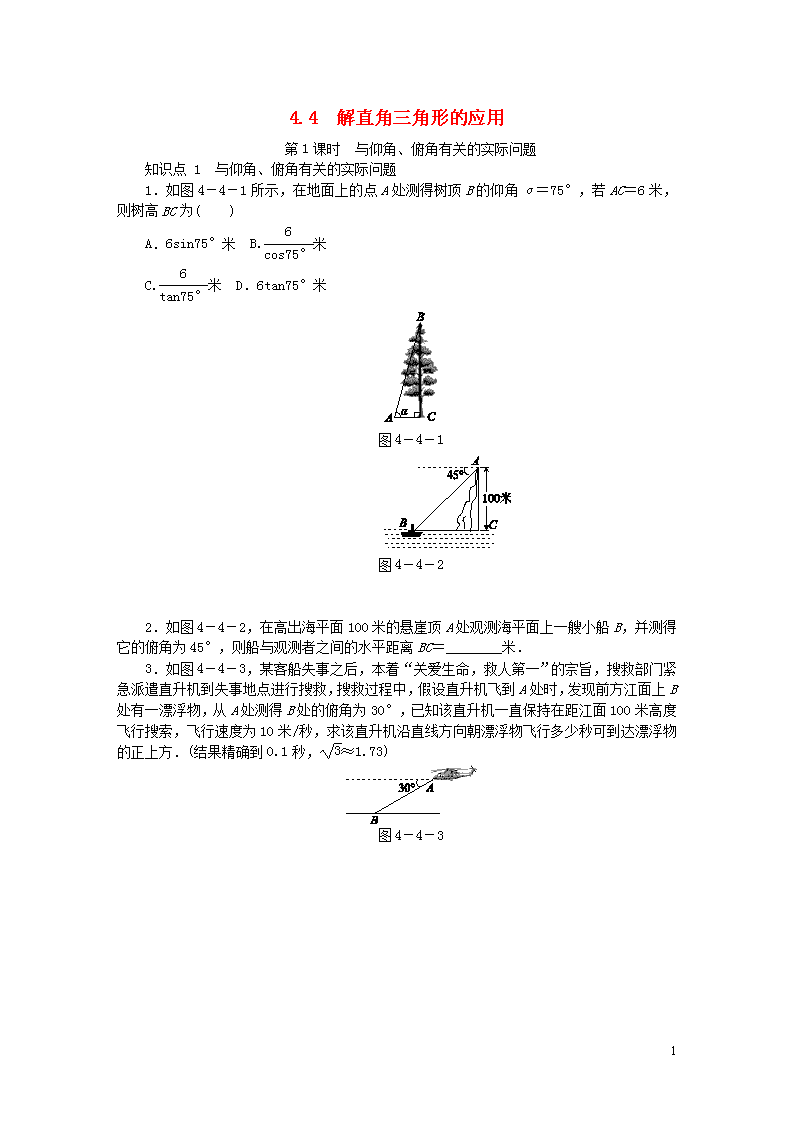
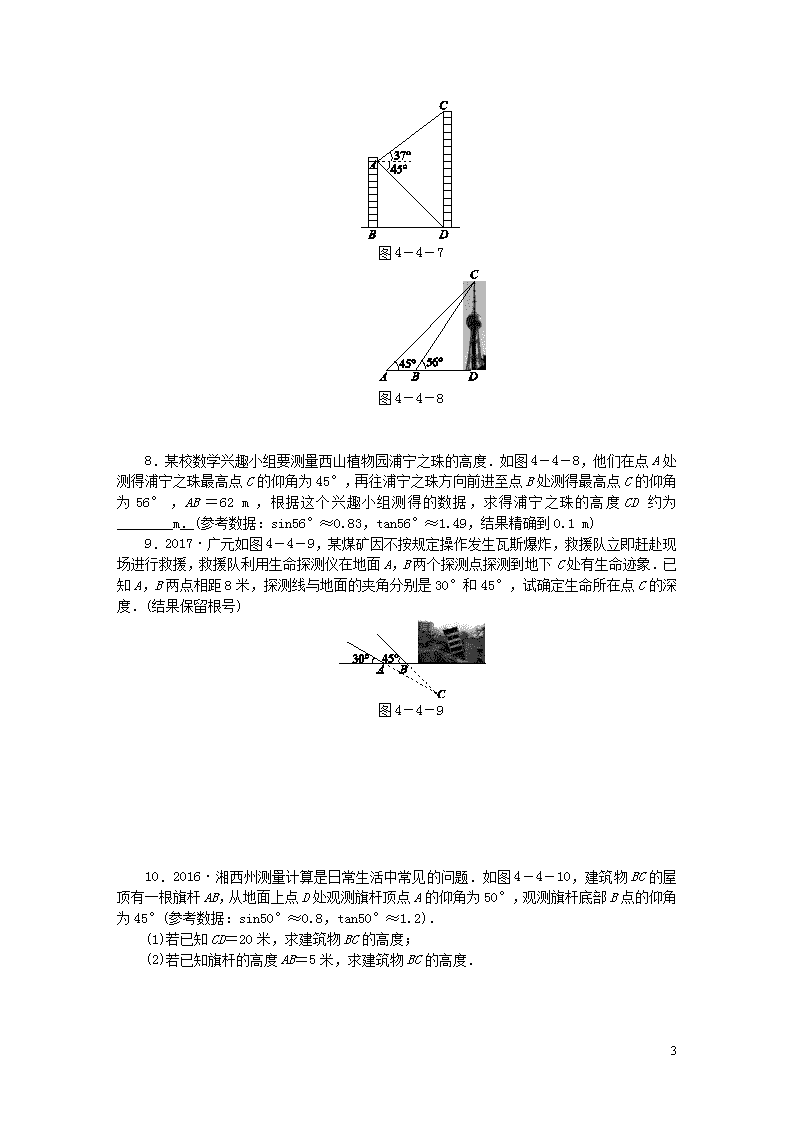
‎4.4　解直角三角形的应用 第1课时 与仰角、俯角有关的实际问题 知识点 1　与仰角、俯角有关的实际问题 ‎1．如图4－4－1所示，在地面上的点A处测得树顶B的仰角α＝75°，若AC＝‎6米，则树高BC为(　　)‎ A．6sin75°米 B.米 C.米 D．6tan75°米 ‎　‎ 图4－4－1‎ ‎　　　　　‎ 图4－4－2‎ ‎2．如图4－4－2，在高出海平面‎100米的悬崖顶A处观测海平面上一艘小船B，并测得它的俯角为45°，则船与观测者之间的水平距离BC＝________米．‎ ‎3．如图4－4－3，某客船失事之后，本着“关爱生命，救人第一”的宗旨，搜救部门紧急派遣直升机到失事地点进行搜救，搜救过程中，假设直升机飞到A处时，发现前方江面上B处有一漂浮物，从A处测得B处的俯角为30°，已知该直升机一直保持在距江面‎100米高度飞行搜索，飞行速度为‎10米/秒，求该直升机沿直线方向朝漂浮物飞行多少秒可到达漂浮物的正上方．(结果精确到0.1秒，≈1.73)‎ 图4－4－3‎ 7‎ 知识点 2　与夹角有关的实际问题 ‎4．如图4－4－4，将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下，使木桩向上运动，已知楔子斜面的倾斜角为20°，若楔子沿水平方向前移‎8 cm(如箭头所示)，则木桩上升了(　　)‎ 图4－4－4‎ A．8tan20° cm B. cm C．8sin20° cm D．8cos20° cm ‎5．2017·丽水如图4－4－5是某小区的一个健身器材，已知BC＝‎0.15 m，AB＝‎2.70 m，∠BOD＝70°，求端点A到地面CD的距离．(精确到‎0.1 m)(参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75)‎ 图4－4－5‎ 图4－4－6‎ ‎6．2017·深圳如图4－4－6，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为‎20 m，DE的长为‎10 m，则树AB的高度是(　　)‎ A．‎20 ‎ m B．‎‎30 m C．‎30 ‎ m D．‎‎40 m ‎7．2017·阜新改编如图4－4－7，从楼AB的A处测得对面楼CD的顶部C的仰角为37°，底部D的俯角为45°，两楼的水平距离BD为‎24 m，那么楼CD的高度约为________m．(结果精确到‎1 m，参考数据：sin37°≈0.602，cos37°≈0.799，tan37°≈0.754)‎ 7‎ 图4－4－7‎ ‎　　　‎ 图4－4－8‎ ‎8．某校数学兴趣小组要测量西山植物园浦宁之珠的高度．如图4－4－8，他们在点A处测得浦宁之珠最高点C的仰角为45°，再往浦宁之珠方向前进至点B处测得最高点C的仰角为56°，AB＝‎62 m，根据这个兴趣小组测得的数据，求得浦宁之珠的高度CD约为________m．(参考数据：sin56°≈0.83，tan56°≈1.49，结果精确到‎0.1 m)‎ ‎9．2017·广元如图4－4－9，某煤矿因不按规定操作发生瓦斯爆炸，救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A，B两个探测点探测到地下C处有生命迹象．已知A，B两点相距‎8米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度．(结果保留根号)‎ 图4－4－9‎ ‎10．2016·湘西州测量计算是日常生活中常见的问题．如图4－4－10，建筑物BC的屋顶有一根旗杆AB，从地面上点D处观测旗杆顶点A的仰角为50°，观测旗杆底部B点的仰角为45°(参考数据：sin50°≈0.8，tan50°≈1.2)．‎ ‎(1)若已知CD＝‎20米，求建筑物BC的高度；‎ ‎(2)若已知旗杆的高度AB＝‎5米，求建筑物BC的高度．‎ 7‎ 图4－4－10‎ ‎ ‎ ‎11．张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图4－4－11，山坡与水平面成30°角(即∠MAN＝30°)，在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进‎20米，到达B处，又测得大树顶端点C的仰角为60°(图中各点均在同一平面内)，求这棵大树CD的高度．(结果精确到‎0.1米，参考数据：≈1.732)‎ 图4－4－11‎ ‎　　　　‎ 详解详析 7‎ ‎1．D ‎2．100　[解析] 由题意得，在Rt△ABC中，∠ABC＝45°，AC＝‎100米，‎ ‎∴BC＝AC＝‎100米．‎ ‎3．解：过点B作BD⊥AD于点D，则BD＝‎100米，‎ 在Rt△ABD中，tan∠BAD＝，‎ ‎∴AD＝＝‎100 ‎米．‎ ‎∵直升机的飞行速度为‎10米/秒，‎ ‎∴飞行时间为100 ÷10＝10 ≈17.3(秒)，‎ ‎∴该直升机沿直线方向朝漂浮物飞行约17.3秒可到达漂浮物的正上方．‎ ‎4．A ‎5．解：过点A作AE⊥CD于点E，过点B作BF⊥AE于点F，则四边形EFBC是矩形．‎ ‎∵OD⊥CD，‎ ‎∴AE∥OD，‎ ‎∴∠A＝∠BOD＝70°.‎ 在Rt△AFB中，∵AB＝2.70 m，‎ ‎∴AF＝2.70×cos70°≈2.70×0.34＝0.918(m)，‎ ‎∴AE＝AF＋FE＝AF＋BC≈0.918＋0.15＝1.068≈1.1(m)．‎ 答：端点A到地面CD的距离约为1.1 m.‎ ‎6．B　7.42‎ ‎8．188.5　[解析] 根据题意得∠CAD＝45°，∠CBD＝56°，AB＝62.‎ ‎∵在Rt△ACD中，∠ACD＝∠CAD＝45°，‎ ‎∴AD＝CD.‎ ‎∵AD＝AB＋BD，‎ ‎∴BD＝AD－AB＝CD－62.‎ ‎∵在Rt△BCD中，tan∠CBD＝，‎ ‎∴BD＝，‎ ‎∴＝CD－62，∴CD≈188.5.‎ 即浦宁之珠的高度CD约为188.5 m.‎ ‎9．解：过点C作CD⊥AB交AB的延长线于点D，如图所示，‎ 7‎ 由已知可得，AB＝8米，∠CBD＝45°，∠CAD＝30°，‎ ‎∴AD＝，BD＝，‎ ‎∴AB＝AD－BD＝－，‎ 即8＝－，‎ 解得CD＝(4 ＋4)米，‎ 即生命所在点C的深度是(4 ＋4)米．‎ ‎10．解： (1)由题意得∠ACD＝90°，∠BDC＝45°，∴BC＝CD·tan∠BDC＝20×1＝20(米)．‎ 答：建筑物BC的高度为20米．‎ ‎(2)设CD＝x米，同(1)得BC＝CD＝x米，AC≈1.2x米．∵AB＝‎5米，∴x＋5＝1.2x，解得x＝25，∴BC＝‎25米．‎ 答：建筑物BC的高度约为25米．‎ ‎11．解：如图，过点B作BE⊥CD交CD的延长线于点E，则BE∥AN.‎ ‎∵∠CAN＝45°，∠MAN＝30°，‎ ‎∴∠CAB＝15°.‎ ‎∵BE∥AN，‎ ‎∴∠DBE＝∠MAN＝30°.‎ ‎∵∠CBE＝60°，∴∠CBD＝30°.‎ ‎∵∠CBD＝∠CAB＋∠ACB，‎ ‎∴∠CAB＝∠ACB＝15°，‎ ‎∴AB＝BC＝20.‎ 在Rt△BCE中，∠CBE＝60°，BC＝20，‎ ‎∴CE＝BC·sin∠CBE＝20×＝10 ，‎ BE＝BC·cos∠CBE＝20×＝10.‎ 在Rt△DBE中，∠DBE＝30°，BE＝10，‎ ‎∴DE＝BE·tan∠DBE＝10×＝，‎ ‎∴CD＝CE－DE＝10 －≈11.5(米)．‎ 7‎ 答：这棵大树CD的高度大约为11.5米． ‎ 7‎