九年级数学上册第五章投影与视图阶段复习习题课件新版北师大版

九年级数学上册第五章投影与视图阶段复习习题课件新版北师大版

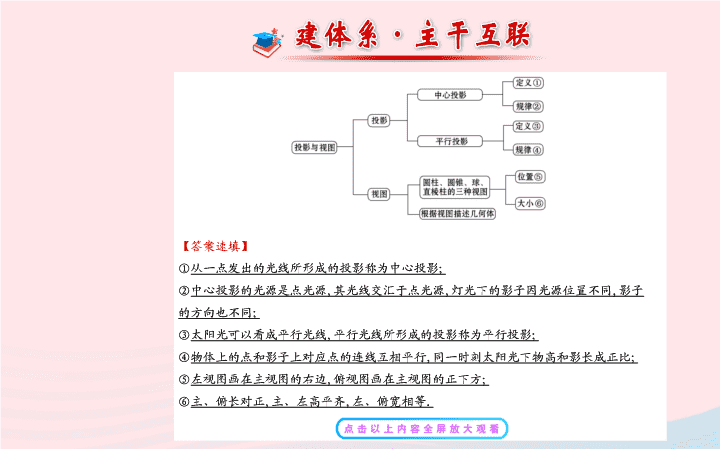
阶段复习课 第 五 章 主题 1 投影及其应用 【 主题训练 1】 (2013 · 陕西中考 ) 一天晚上 , 李明和张龙利用灯光下的影子长来测量一路 灯 D 的高度 . 如图 , 当李明走到点 A 处时 , 张龙测 得李明直立时身高 AM 与其影子长 AE 正好相等 , 接着李明沿 AC 方向继续向前走 , 走到点 B 处时 , 李明直立身高 BN 的影子恰好是线段 AB, 并测得 AB=1.25m, 已知李明直立时的身高为 1.75m, 求路灯的高 CD 的长 .( 结果精确到 0.1m) 【 自主解答 】 设 CD 长为 xm, ∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA, ∴AM∥CD,BN∥CD,∴EC=CD=x,△ABN∽△ACD, ∴ 解得 x=6.125≈6.1, ∴ 路灯的高 CD 的长约为 6.1m. 【 主题升华 】 1. 分类 :(1) 平行投影 : 由平行光线形成的投影 . (2) 中心投影 : 由点光源发出的光线形成的投影 . 2. 性质 : (1) 平行投影 : 同一时刻 , 垂直于投影面的物体 , 物高与影长成比例 . (2) 中心投影 : 物体平行于投影面时 , 原物体与投影关于点光源位似 . 1.(2013 · 白银中考 ) 如图 , 路灯距离地面 8m, 身高 1.6m 的小明站在距离灯的底部 ( 点 O)20m 的 A 处 , 则小明的影子 AM 长 　　　　 m. 【 解析 】 设 AM=x, 由题意可知△ ABM∽△OCM, 所以 OC=8,AB=1.6,OA=20,AM=x, OM=OA+AM=20+x, 解得 x=5, 因此 AM 的长是 5m. 答案 : 5 2.(2011 · 昭通中考 ) 如图所示 , 某班上体育课 , 甲、乙两名同学分别站在 C,D 的位置时 , 乙的影子恰好在甲的影子里边 , 已知甲身高 1.8m, 乙身高 1.5m, 甲的影长是 6m, 则甲、乙同学相距 　　　　 m. 【 解析 】 由题意得 ,△ADE∽△ACB, 所以 AC=6m,BC=1.8m,DE=1.5m, 所以 AD=5m, 所以 CD=6-5=1(m). 答案 : 1 【 知识归纳 】 1. 平行投影的有关计算问题大都与三角形及三角形相似联系在一起 , 在解答时要注意投影与三角形相似等性质的综合应用 . 2. 在平行投影下 , 无论物体与投影面的位置关系怎样及光线与投影面的位置关系如何 , 都不改变物体中线的平行关系 . 3.(2013 · 甘肃中考 ) 如图是住宅区内的两幢 楼 , 它们的高 AB=CD=30m, 两楼间的距离 AC=30m, 现需了解甲楼对乙楼的采光的影响情况 . (1) 当太阳光与水平线的夹角为 30° 角时 , 求甲楼的影子在乙楼上有多高 ( 精确到 0.1m, =1.73). (2) 若要甲楼的影子刚好不落在乙楼的墙上 , 此时太阳与水平线的夹角为多少度 ? 【 解析 】 (1) 如图 , 延长 QB 交 DC 于 E, 作 EF⊥AB, 交 AB 于 F, 在 Rt△BEF 中 ,∵EF=AC=30m,∠FEB=30°, ∴BE=2BF. 设 BF=xm, 则 BE=2xm. 根据勾股定理知 BE 2 =BF 2 +EF 2 , ∴(2x) 2 =x 2 +30 2 ,∴x=10 ( 负值舍去 ),∴x≈17.3. 因此 ,EC=30-17.3=12.7(m). (2) 当甲幢楼的影子刚好落在点 C 处时 ,△ABC 为等腰直角三角形 , 因此 , 当太阳光与水平线夹角为 45° 时 , 甲楼的影子刚好不落在乙楼的墙上 . 4.(2014 · 大连模拟 ) 两棵树的高度分别为 AB=6m,CD=8m, 两树的根部间的距离 AC=4m, 小强正在距树 AB20m 的点 P 处从左向右前进 , 如果小强的眼睛与地面距离为 1.6m, 当小强前进多少米时 , 就恰好不能看到 CD 的树顶 D? 【 解析 】 设 FG=xm, 那么 FH=x+GH=x+AC=x+4(m). ∵AB=6m,CD=8m, 小强的眼睛与地面的距离为 1.6m, ∴BG=4.4m,DH=6.4m, ∵BA⊥PC,CD⊥PC,∴AB∥CD, ∴FG∶FH=BG∶DH, 即 FG · DH=FH · BG, ∴6.4x=4.4(x+4),∴x=8.8, 20-8.8=11.2(m). 答 : 前进 11.2m 时恰好不能看到 CD 的树顶 D. 主题 2 几何体的三种视图 【 主题训练 2】 (2013 · 嘉兴中考 ) 如图 , 由三个小立方块搭成的俯视图是　 ( 　　 ) 【 自主解答 】 选 A. 从上面观察这个几何体 , 得到的平面图形是左边一个正方形 , 右边一个正方形 , 且大小相同 . 因此 , 符合题意的俯视图是 A. 【 备选例题 】 (2013 · 牡丹江中考 ) 由一些大小相同的小正方体搭成的几何体的左视图和俯视图 , 如图所示 , 则搭成该几何体的小正方体的个数最少是　 ( 　　 ) A.4 　　 B.5 　　 C.6 　 D.7 【 解析 】 选 C. 根据左视图和俯视图可知该几何体每个位置小正方体的个数可能有以下三种情形 ( 小正方体个数相同的只提供一种 ), 其中小正方体的个数最少是 6 个 . 2 2 2 2 2 2 1 2 1 2 2 1 【 主题升华 】 1. 三视图与投影的关系 : 三视图是平行光线垂直于投影面时的投影 , 即正投影 . 2. 三视图之间的关系 : (1) 长对正 : 主视图与俯视图的长相等 . (2) 高平齐 : 主视图与左视图的高相等 . (3) 宽相等 : 左视图与俯视图的宽相等 . 1.(2013 · 湛江中考 ) 如图是由 6 个大小相同的正方体组成的几何体 , 它的左视图是　 ( 　　 ) 【 解析 】 选 A. 从左边看 , 左边一列有两个正方体 , 右边有一个 , 故选 A. 2.(2013 · 安徽中考 ) 图中所示的几何体为圆台 , 其主视图正确的是　 ( 　　 ) 【 解析 】 选 A. 根据主视图的概念 , 该物体的主视图是选项 A 中的平面图形 . 3.(2013 · 乐山中考 ) 一个立体图形的三种视图如图所示 , 根据图中数据求得这个立体图形的表面积为　 ( 　　 ) A.2π 　　 B.6π 　　 C.7π 　　 D.8π 【 解析 】 选 D. 根据三种视图知该几何体为圆柱 , 圆柱的侧面积为 :2π×3=6π, 底面积为 :π× =π, 所以圆柱的表面积为 :6π+2π=8π. 4.(2013 · 龙东中考 ) 由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示 , 则组成这个几何体的小正方体的个数最多有　 ( 　　 ) A.4 B.5 C.6 D.7 【 解析 】 选 C. 由俯视图可知 , 该几何体有两行两列 , 再由主视图可知第一层有 4 个小立方块 ; 第 2 层的左边一列最多有 2 个小立方块 , 所以组成这个几何体的小正方体的个数最多是 4+2=6. 5.(2013 · 佛山中考 ) 并排放置的等底等高的圆锥和圆柱 ( 如图 ) 的主视图是　 ( 　　 ) 【 解析 】 选 B.A 的两个图是图中两个几何体的俯视图 , 不是主视图 ;C 是左视图 ,D 是从右侧观察的结果 , 但图中缺少虚线 , 故都不正确 , 只有 B 正确 . 6.(2013 · 台州中考 ) 有一篮球如图放置 , 其主视图为　 ( 　　 ) 【 解析 】 选 B. 从篮球的前方 “ 正对着 ” 观察得到的形状是圆 , 故选 B.