- 2021-11-06 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学一轮复习知识点+题型专题讲义10 二次根式(学生版)
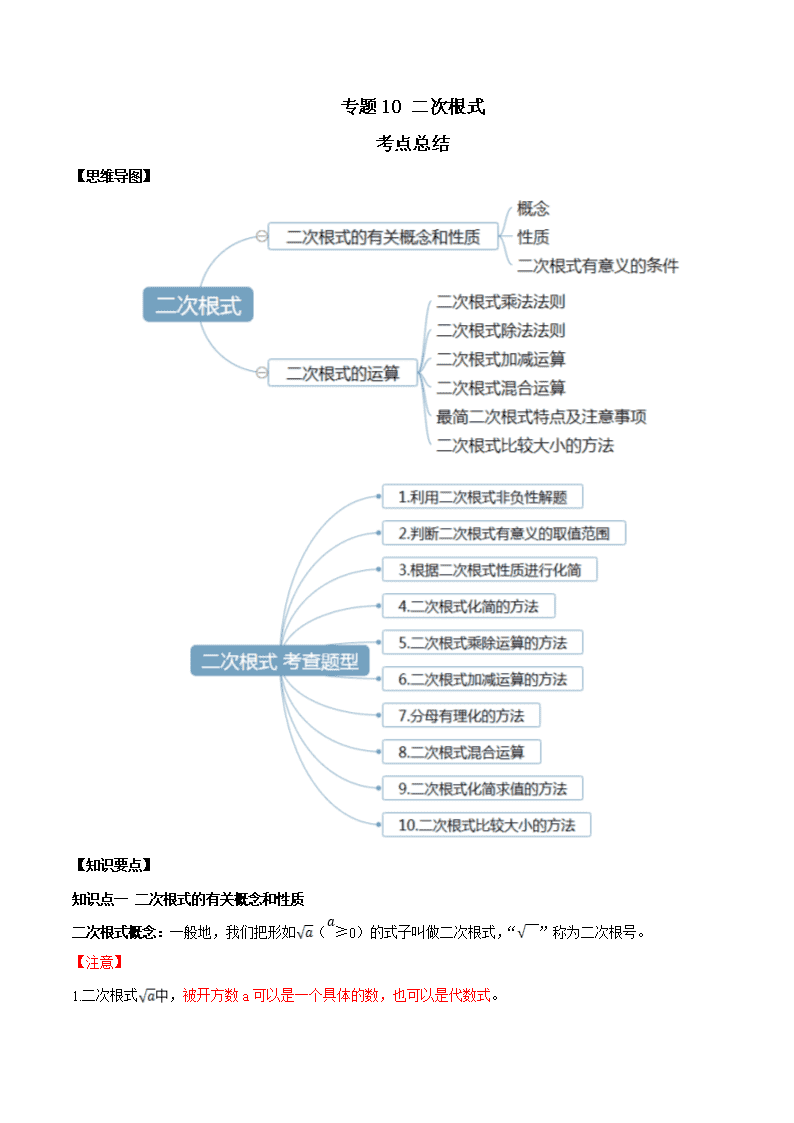
专题 10 二次根式 考点总结 【思维导图】 【知识要点】 知识点一 二次根式的有关概念和性质 二次根式概念:一般地,我们把形如 ( � ≥0)的式子叫做二次根式,“ ”称为二次根号。 【注意】 1.二次根式 ,被开方数 a 可以是一个具体的数,也可以是代数式。 2.二次根式 是一个非负数。 3.二次根式与算术平方根有着内在联系, ( � ≥0)就表示 a 的算术平方根。 二次根式有意义的条件:由二次根式的意义可知,当 a≧0 时, 有意义,是二次根式,所以要使二次根式 有意义,只要使被开方数大于或等于零即可。 二次根式的性质: 1.含有两种相同的运算,两者都需要进行平方和开方。 2.结果的取值范围相同,两者的结果都是非负数。 3.当 a≧0 时, 考查题型一 利用二次根式非负性解题 1.(2013·四川中考真题)已知实数 x,y,m 满足 x 2 | 3x y m | 0 ,且 y 为负数,则 m 的取值范围 是( ) A.m>6 B.m<6 C.m>﹣6 D.m<﹣6 2.(2016·四川中考真题)若 1a +b2﹣4b+4=0,则 ab 的值等于( ) A.﹣2 B.0 C.1 D.2 3.(2012·湖北中考真题)若 2 9x y 与|x﹣y﹣3|互为相反数,则 x+y 的值为( ) A.3 B.9 C.12 D.27 考查题型二 判断二次根式有意义的取值范围 1.(2013·四川中考真题)若代数式 有意义,则实数 x 的取值范围是( ) A. B. C. D. 且 2.(2018·内蒙古中考真题)代数式 13 1x x 中 x 的取值范围在数轴上表示为( ) A. B. C. D. 3.(2018·山东中考真题)若式子 2 m 2 (m 1) 有意义,则实数 m 的取值范围是( ) A. m 2 B. m 2 且 m 1 C. m 2 D. m 2 且 m 1 考查题型三 根据二次根式性质进行化简 1.(2012·湖南中考真题)实数 a、b 在数轴上的位置如图所示,且|a|>|b|,则化简 2a a b 的结果为( ) A.2a+b B.-2a+b C.b D.2a-b 2.(2016·山东中考真题)实数 a,b 在数轴上对应点的位置如图所示,化简|a|+ 2( )a b 的结果是( ) A.﹣2a-b B.2a﹣b C.﹣b D.b 3.(2011·北京中考真题)如果 ,则 a 的取值范围是( ) A. B. C. D. 4.(2015·湖北中考真题)当 1<a<2 时,代数式 2( 2)a +|1-a|的值是( ) A.-1 B.1 C.2a-3 D.3-2a 5.(2011·四川中考真题)已知 2 5 5 2 3y x x ,则 2xy 的值为( ) A. 15 B.15 C. 15 2 D.15 2 知识点二 二次根式的运算 二次根式的乘法法则: 【注意】 1、要注意 这个条件,只有 a,b 都是非负数时法则成立。 : 3、乘法交换律在二次根式中仍然适用。 二次根式的乘法法则变形(积的算术平方根): 化简二次根式的步骤(易错点): 1.把被开方数分解因式(或因数) ; 2.把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积; 3.如果因式中有平方式(或平方数),应用关系式(√ � )^2= � ( � ≥0)把这个因式(或因数)开出来,将二次根 式化简。 二次根式的除法法则: 【注意】 1、要注意 这个条件,因为 b=0 时,分母为 0,没有意义。 2、在实际解题时,若不考虑 a、b 的正负性,直接得 是错误的。 二次根式的除法法则变形(商的算术平方根): 二次根式的特点: 1.被开方数不含分母,例: ; 2.被开方数中不含能开得尽方的因数或因式,例: 。 【二次根式运算中的注意事项】 一般将最后结果化为最简二次根式,并且分母中不含二次根式。 二次根式的加减:先将二次根式化为最简二次根式,再把被开方数相同的二次根式(即同类二次根式)进 行合并。(合并方法为:将系数相加减,二次根式部分不变),不能合并的直接抄下来。 二次根式比较大小: 1、若 ,则有 ; 2、若 ,则有 . 3、将两个根式都平方,比较平方后的大小,对应平方前的大小。 二次根式混合运算顺序:先计算括号内,再乘方(开方),再乘除,再加减。 注意:运算结果是根式的,一般应表示为最简二次根式。 考查题型四 二次根式化简的方法 1.(2016·甘肃中考真题)下列根式中是最简二次根式的是 ( ) A. 2 3 B. 3 C. 9 D. 12 2.(2018·甘肃中考真题)下列二次根式中,是最简二次根式的是 ( ) A. 18 B. 13 C. 27 D. 12 3.(2011·广东中考真题)下列二次根式中,最简二次根式的是( ) A. 1 5 B. 0.5 C. 5 D. 50 考查题型五 二次根式乘除运算的方法 1.(2015·安徽中考真题)计算 × 的结果是( ) A. B.4 C. D.2 2.(2013·海南中考真题)下列各数中,与 的积为有理数的是( ) A. B. C. D. 3.(2018·江苏中考真题)计算: 1 82 =_____. 4.(2018·湖南中考真题) 12 3= ________. 5.(2019·安徽中考真题)计算 18 2 的结果是__________. 6.(2015·广西中考真题)计算: 1 27=3 _________. 7.(2016·山东中考真题)计算: = . 考察题型六 二次根式加减运算的方法 1.(2018·山东中考真题) 12 与最简二次根式 5 1a 是同类二次根式,则 a=_____. 2.(2019·江苏中考真题)计算: . 3.(2018·黑龙江中考真题)计算 6 5 ﹣10 1 5 的结果是_____. 4.(2018·辽宁中考真题)计算: 27 ﹣ 12 =__. 5.(2018·湖北中考真题)计算 ( 3 2) 3 的结果是_____ 考查题型七 分母有理化的方法 1.(2015·江苏中考真题)计算 5 15 3 的结果是 . 2.(2019·江苏中考真题)计算 14 28 7 的结果是_____________. 3.(2015·湖南中考真题)把 进行化简,得到的最简结果是 (结果保留根号)。 4.(2019·山东中考真题)计算: 024 8 ( 3) 2 =___________. 考查题型八 二次根式混合运算 1.(2019·山东中考真题)计算: 21 3 1| 3 2 |2 2 18 _________. 2.(2015·辽宁中考真题)计算 2(1 2) 18 的值是__. 3.(2015·内蒙古中考真题)计算: 1( 27 ) 33 = . 4.(2015·山东中考真题)计算( + )( ﹣ )的结果为 . 考查题型九 二次根式化简求值的方法 1.(2014·四川中考真题)已知 ,则 x12+x22= . 2.(2019·山东中考真题)已知 6 2x ,那么 2 2 2x x 的值是_____. 3.(2016·湖北中考真题)当 a= ﹣1 时,代数式 的值是 . 4.(2015·吉林中考真题)先化简,再求值: ,其中 . 考查题型十 二次根式比较大小的方法 1.(2018·河南中考模拟)比较大小:2 5 ____3 2 (填“>”、“<”或“=”). 2.(2019·陕西中考模拟)比较大小:5 2 _____ 13 . 3.(2019·陕西中考模拟)比较大小: 2 5 ______ 3 2 .查看更多