四川省甘孜州2020年中考数学试卷

四川省甘孜州2020年中考数学试卷

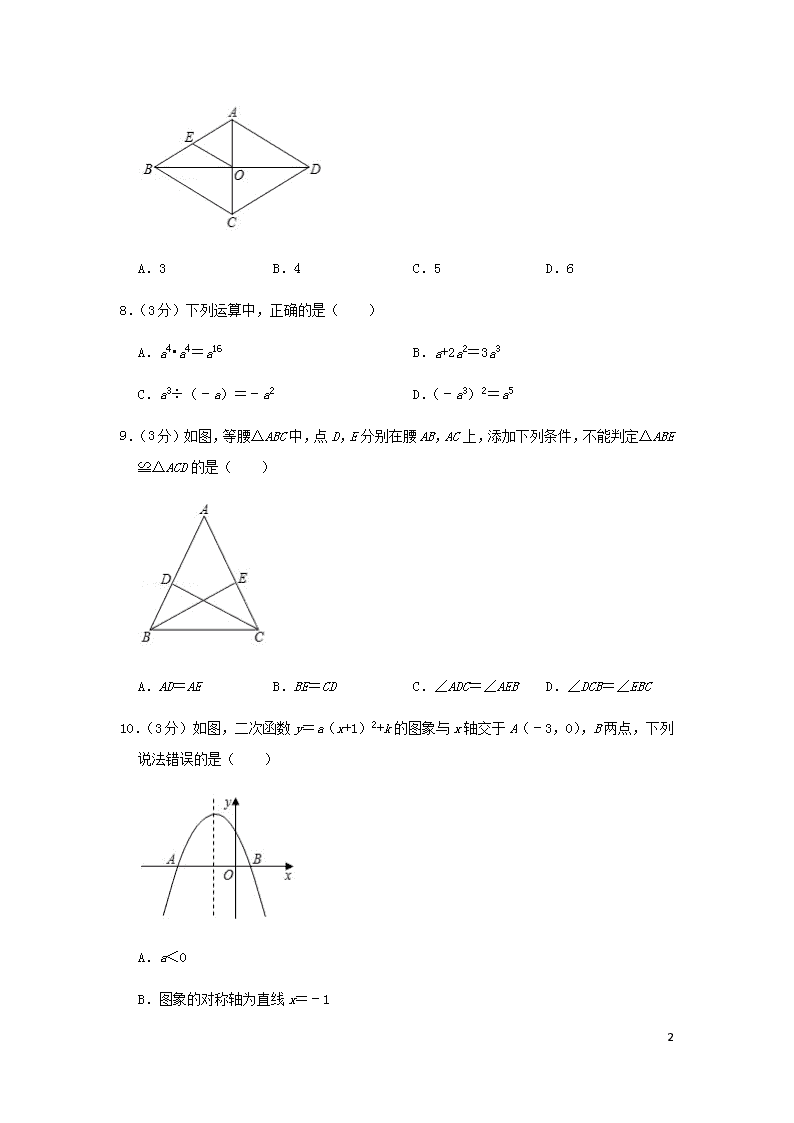
四川省甘孜州2020年中考数学试卷 一、选择题（本大题共10个小题，每小题3分，共30分．每小题均有四个选项，其中只有一项符合题目要求）‎ ‎1．（3分）气温由﹣5℃上升了4℃时的气温是（　　）‎ A．﹣1℃ B．1℃ C．﹣9℃ D．9℃‎ ‎2．（3分）如图摆放的下列几何体中，左视图是圆的是（　　）‎ A． B． ‎ C． D．‎ ‎3．（3分）月球与地球之间的平均距离约为38.4万公里，38.4万用科学记数法表示为（　　）‎ A．38.4×104 B．3.84×105 C．0.384×106 D．3.84×106‎ ‎4．（3分）函数y＝中，自变量x的取值范围是（　　）‎ A．x＞﹣3 B．x＜3 C．x≠﹣3 D．x≠3‎ ‎5．（3分）在平面直角坐标系中，点（2，﹣1）关于x轴对称的点是（　　）‎ A．（2，1） B．（1，﹣2） C．（﹣1，2） D．（﹣2，﹣1）‎ ‎6．（3分）分式方程﹣1＝0的解为（　　）‎ A．x＝1 B．x＝2 C．x＝3 D．x＝4‎ ‎7．（3分）如图，菱形ABCD中，对角线AC，BD相交于点O，E为AB的中点．若菱形ABCD的周长为32，则OE的长为（　　）‎ 31‎ A．3 B．4 C．5 D．6‎ ‎8．（3分）下列运算中，正确的是（　　）‎ A．a4•a4＝a16 B．a+2a2＝3a3 ‎ C．a3÷（﹣a）＝﹣a2 D．（﹣a3）2＝a5‎ ‎9．（3分）如图，等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件，不能判定△ABE≌△ACD的是（　　）‎ A．AD＝AE B．BE＝CD C．∠ADC＝∠AEB D．∠DCB＝∠EBC ‎10．（3分）如图，二次函数y＝a（x+1）2+k的图象与x轴交于A（﹣3，0），B两点，下列说法错误的是（　　）‎ A．a＜0 ‎ B．图象的对称轴为直线x＝﹣1 ‎ 31‎ C．点B的坐标为（1，0） ‎ D．当x＜0时，y随x的增大而增大 二、填空题（本大题共4个小题，每小题4分，共16分）‎ ‎11．（4分）计算：|﹣5|＝　 　．‎ ‎12．（4分）如图，在▱ABCD中，过点C作CE⊥AB，垂足为E，若∠EAD＝40°，则∠BCE的度数为　 　．‎ ‎13．（4分）某班为了解同学们一周在校参加体育锻炼的时间，随机调查了10名同学，得到如下数据：‎ 锻炼时间（小时）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 人数 ‎1‎ ‎4‎ ‎3‎ ‎2‎ 则这10名同学一周在校参加体育锻炼时间的平均数是　 　小时．‎ ‎14．（4分）如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则OH的长度为　 　．‎ 三、解答题（本大题共6个小题，共54分）‎ ‎15．（12分）（1）计算：﹣4sin60°+（2020﹣π）0．‎ 31‎ ‎（2）解不等式组：‎ ‎16．（6分）化简：（﹣）•（a2﹣4）．‎ ‎17．（8分）热气球的探测器显示，从热气球A处看大楼BC顶部C的仰角为30°，看大楼底部B的俯角为45°，热气球与该楼的水平距离AD为60米，求大楼BC的高度．（结果精确到1米，参考数据：≈1.73）‎ ‎18．（8分）如图，一次函数y＝x+1的图象与反比例函数y＝的图象相交于A（2，m）和B两点．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）求点B的坐标．‎ ‎19．（10分）为了解同学们最喜欢一年四季中的哪个季节，数学社在全校随机抽取部分同学进行问卷调查，根据调查结果，得到如下两幅不完整的统计图．‎ 31‎ 根据图中信息，解答下列问题：‎ ‎（1）此次调查一共随机抽取了　 　名同学；扇形统计图中，“春季”所对应的扇形的圆心角的度数为　 　；‎ ‎（2）若该学校有1500名同学，请估计该校最喜欢冬季的同学的人数；‎ ‎（3）现从最喜欢夏季的3名同学A，B，C中，随机选两名同学去参加学校组织的“我爱夏天”演讲比赛，请用列表或画树状图的方法求恰好选到A，B去参加比赛的概率．‎ ‎20．（10分）如图，AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．‎ ‎（1）求证：∠CAD＝∠CAB；‎ ‎（2）若＝，AC＝2，求CD的长．‎ 一、填空题（本大题共5个小题，每小题4分，共20分）‎ ‎21．（4分）在单词“mathematics”中任意选择一个字母，选到字母“a”的概率是　 　．‎ ‎22．（4分）若m2﹣2m＝1，则代数式2m2﹣4m+3的值为　 　．‎ ‎23．（4分）三角形的两边长分别为4和7，第三边的长是方程x2﹣8x 31‎ ‎+12＝0的解，则这个三角形的周长是　 　．‎ ‎24．（4分）如图，有一张长方形纸片ABCD，AB＝8cm，BC＝10cm，点E为CD上一点，将纸片沿AE折叠，BC的对应边B′C′恰好经过点D，则线段DE的长为　 　cm．‎ ‎25．（4分）如图，在平面直角坐标系xOy中，一次函数y＝x+1的图象与反比例函数y＝的图象交于A，B两点，若点P是第一象限内反比例函数图象上一点，且△ABP的面积是△AOB的面积的2倍，则点P的横坐标为　 　．‎ 五、解答题（本大题共3个小题，共30分）‎ ‎26．（8分）某商品的进价为每件40元，在销售过程中发现，每周的销售量y（件）与销售单价x（元）之间的关系可以近似看作一次函数y＝kx+b，且当售价定为50元/件时，每周销售30件，当售价定为70元/件时，每周销售10件．‎ ‎（1）求k，b的值；‎ ‎（2）求销售该商品每周的利润w（元）与销售单价x（元）之间的函数解析式，并求出销售该商品每周可获得的最大利润．‎ ‎27．（10分）如图，Rt△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转得到△DEC，点D落在线段AB上，连接BE．‎ 31‎ ‎（1）求证：DC平分∠ADE；‎ ‎（2）试判断BE与AB的位置关系，并说明理由；‎ ‎（3）若BE＝BD，求tan∠ABC的值．‎ ‎28．（12分）如图，在平面直角坐标系xOy中，直线y＝kx+3分别交x轴、y轴于A，B两点，经过A，B两点的抛物线y＝﹣x2+bx+c与x轴的正半轴相交于点C（1，0）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若P为线段AB上一点，∠APO＝∠ACB，求AP的长；‎ ‎（3）在（2）的条件下，设M是y轴上一点，试问：抛物线上是否存在点N，使得以A，P，M，N为顶点的四边形为平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．‎ 31‎ ‎2020年四川省甘孜州中考数学试卷 参考答案与试题解析 一、选择题（本大题共10个小题，每小题3分，共30分．每小题均有四个选项，其中只有一项符合题目要求）‎ ‎1．（3分）气温由﹣5℃上升了4℃时的气温是（　　）‎ A．﹣1℃ B．1℃ C．﹣9℃ D．9℃‎ ‎【分析】根据题意列出算式，计算即可求出值．‎ ‎【解答】解：根据题意得：﹣5+4＝﹣1，‎ 则气温由﹣5℃上升了4℃时的气温是﹣1℃．‎ 故选：A．‎ ‎【点评】此题考查了有理数的加法，熟练掌握运算法则是解本题的关键．‎ ‎2．（3分）如图摆放的下列几何体中，左视图是圆的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在左视图中．‎ ‎【解答】解：A．正方体的左视图是正方形，故本选项不合题意；‎ B．圆柱的左视图是矩形，故本选项不合题意；‎ C．球的的左视图是圆，故本选项符号题意；‎ D．圆锥的左视图是等腰三角形，故本选项不合题意；‎ 31‎ 故选：C．‎ ‎【点评】本题考查了三视图的知识，左视图是从物体的左面看得到的视图．‎ ‎3．（3分）月球与地球之间的平均距离约为38.4万公里，38.4万用科学记数法表示为（　　）‎ A．38.4×104 B．3.84×105 C．0.384×106 D．3.84×106‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：38.4万＝384000＝3.84×105，‎ 故选：B．‎ ‎【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎4．（3分）函数y＝中，自变量x的取值范围是（　　）‎ A．x＞﹣3 B．x＜3 C．x≠﹣3 D．x≠3‎ ‎【分析】根据分母不等于0列式计算即可得解．‎ ‎【解答】解：由题意得x+3≠0，‎ 解得x≠﹣3．‎ 故选：C．‎ ‎【点评】本题考查了函数自变量的范围，一般从三个方面考虑：‎ ‎（1）当函数表达式是整式时，自变量可取全体实数；‎ ‎（2）当函数表达式是分式时，考虑分式的分母不能为0；‎ ‎（3）当函数表达式是二次根式时，被开方数非负．‎ ‎5．（3分）在平面直角坐标系中，点（2，﹣1）关于x轴对称的点是（　　）‎ A．（2，1） B．（1，﹣2） C．（﹣1，2） D．（﹣2，﹣1）‎ 31‎ ‎【分析】直接利用关于x轴对称点的性质进而得出答案．‎ ‎【解答】解：点（2，﹣1）关于x轴对称的点是：（2，1）．‎ 故选：A．‎ ‎【点评】此题主要考查了关于x轴对称点的性质，正确记忆横纵坐标的关系是解题关键．‎ ‎6．（3分）分式方程﹣1＝0的解为（　　）‎ A．x＝1 B．x＝2 C．x＝3 D．x＝4‎ ‎【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ ‎【解答】解：分式方程﹣1＝0，‎ 去分母得：3﹣（x﹣1）＝0，‎ 去括号得：3﹣x+1＝0，‎ 解得：x＝4，‎ 经检验x＝4是分式方程的解．‎ 故选：D．‎ ‎【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．‎ ‎7．（3分）如图，菱形ABCD中，对角线AC，BD相交于点O，E为AB的中点．若菱形ABCD的周长为32，则OE的长为（　　）‎ A．3 B．4 C．5 D．6‎ 31‎ ‎【分析】由菱形的性质得出AB＝BC＝CD＝AD＝8，AC⊥BD，则∠AOB＝90°，由直角三角形斜边上的中线性质即可得出答案．‎ ‎【解答】解：∵四边形ABCD是菱形，‎ ‎∴AB＝BC＝CD＝AD，AC⊥BD，‎ ‎∴∠AOB＝90°，‎ ‎∵菱形ABCD的周长为32，‎ ‎∴AB＝8，‎ ‎∵E为AB边中点，‎ ‎∴OE＝AB＝4．‎ 故选：B．‎ ‎【点评】本题考查了菱形的性质以及直角三角形斜边上的中线性质等知识，解答本题的关键掌握菱形的性质和直角三角形斜边上的中线性质．‎ ‎8．（3分）下列运算中，正确的是（　　）‎ A．a4•a4＝a16 B．a+2a2＝3a3 ‎ C．a3÷（﹣a）＝﹣a2 D．（﹣a3）2＝a5‎ ‎【分析】分别根据同底数幂的乘法法则，合并同类项法则，同底数幂的除法法则以及积的乘方运算法则逐一判断即可．‎ ‎【解答】解：A．a4•a4＝a8，故本选项不合题意；‎ B．a与2a2不是同类项，所以不能合并，故本选项不合题意；‎ C．a3÷（﹣a）＝﹣a2，故本选项符合题意；‎ D．（﹣a3）2＝a6，故本选项不合题意；‎ 故选：C．‎ 31‎ ‎【点评】本题主要考查了同底数幂的乘除法，合并同类项以及幂的乘方与积的乘方，熟记相关运算法则是解答本题的关键．‎ ‎9．（3分）如图，等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件，不能判定△ABE≌△ACD的是（　　）‎ A．AD＝AE B．BE＝CD C．∠ADC＝∠AEB D．∠DCB＝∠EBC ‎【分析】利用等腰三角形的性质得∠ABC＝∠ACB，AB＝AC，然后根据全等三角形的判定方法对各选项进行判断．‎ ‎【解答】解：∵△ABC为等腰三角形，‎ ‎∴∠ABC＝∠ACB，AB＝AC，‎ ‎∴当AD＝AE时，则根据“SAS”可判断△ABE≌△ACD；‎ 当∠AEB＝∠ADC，则根据“AAS”可判断△ABE≌△ACD；‎ 当∠DCB＝∠EBC，则∠ABE＝∠ACD，根据“ASA”可判断△ABE≌△ACD．‎ 故选：B．‎ ‎【点评】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法．选用哪一种方法，取决于题目中的已知条件．也考查了等腰三角形的性质．‎ ‎10．（3分）如图，二次函数y＝a（x+1）2+k的图象与x轴交于A（﹣3，0），B两点，下列说法错误的是（　　）‎ 31‎ A．a＜0 ‎ B．图象的对称轴为直线x＝﹣1 ‎ C．点B的坐标为（1，0） ‎ D．当x＜0时，y随x的增大而增大 ‎【分析】根据二次函数的性质解决问题即可．‎ ‎【解答】解：观察图形可知a＜0，由抛物线的解析式可知对称轴x＝﹣1，‎ ‎∵A（﹣3，0），A，B关于x＝﹣1对称，‎ ‎∴B（1，0），‎ 故A，B，C正确，‎ 故选：D．‎ ‎【点评】本题考查二次函数的图象与系数的关系，抛物线与x轴的交点等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．‎ 二、填空题（本大题共4个小题，每小题4分，共16分）‎ ‎11．（4分）计算：|﹣5|＝　5　．‎ ‎【分析】根据绝对值定义去掉这个绝对值的符号即可．‎ ‎【解答】解：|﹣5|＝5．‎ 故答案为：5‎ ‎【点评】绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．‎ 31‎ ‎12．（4分）如图，在▱ABCD中，过点C作CE⊥AB，垂足为E，若∠EAD＝40°，则∠BCE的度数为　50°　．‎ ‎【分析】由平行四边形的性质得出∠B＝∠EAD＝40°，由角的互余关系得出∠BCE＝90°﹣∠B＝50°即可．‎ ‎【解答】解：∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，‎ ‎∴∠B＝∠EAD＝40°，‎ ‎∵CE⊥AB，‎ ‎∴∠BCE＝90°﹣∠B＝50°；‎ 故答案为：50°．‎ ‎【点评】本题考查了平行四边形的性质、角的互余关系；熟练掌握平行四边形的性质，求出∠B的度数是解决问题的关键．‎ ‎13．（4分）某班为了解同学们一周在校参加体育锻炼的时间，随机调查了10名同学，得到如下数据：‎ 锻炼时间（小时）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 人数 ‎1‎ ‎4‎ ‎3‎ ‎2‎ 则这10名同学一周在校参加体育锻炼时间的平均数是　6.6　小时．‎ ‎【分析】根据加权平均数的定义列式计算可得．‎ ‎【解答】解：这10名同学一周在校参加体育锻炼时间的平均数是＝6.6（小时），‎ 31‎ 故答案为：6.6．‎ ‎【点评】本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．‎ ‎14．（4分）如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则OH的长度为　3　．‎ ‎【分析】根据垂径定理由CD⊥AB得到CH＝CD＝4，再根据勾股定理计算出OH＝3．‎ ‎【解答】解：连接OC，‎ ‎∵CD⊥AB，‎ ‎∴CH＝DH＝CD＝×8＝4，‎ ‎∵直径AB＝10，‎ ‎∴OC＝5，‎ 在Rt△OCH中，OH＝＝3，‎ 故答案为3．‎ ‎【点评】本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．‎ 三、解答题（本大题共6个小题，共54分）‎ 31‎ ‎15．（12分）（1）计算：﹣4sin60°+（2020﹣π）0．‎ ‎（2）解不等式组：‎ ‎【分析】（1）先计算二次根式、代入三角函数值、计算零指数幂，再计算乘法，最后计算加减可得；‎ ‎（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．‎ ‎【解答】解：（1）原式＝2﹣4×+1‎ ‎＝2﹣2+1‎ ‎＝1；‎ ‎（2）解不等式x+2＞﹣1，得：x＞﹣3，‎ 解不等式≤3，得：x≤5，‎ 则不等式组的解集为﹣3＜x≤5．‎ ‎【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．‎ ‎16．（6分）化简：（﹣）•（a2﹣4）．‎ ‎【分析】根据分式的减法和乘法可以解答本题．‎ ‎【解答】解：（﹣）•（a2﹣4）‎ ‎＝•（a+2）（a﹣2）‎ ‎＝3a+6﹣a+2‎ 31‎ ‎＝2a+8．‎ ‎【点评】本题考查分式的混合运算，解答本题的关键是明确分式混合运算的计算方法．‎ ‎17．（8分）热气球的探测器显示，从热气球A处看大楼BC顶部C的仰角为30°，看大楼底部B的俯角为45°，热气球与该楼的水平距离AD为60米，求大楼BC的高度．（结果精确到1米，参考数据：≈1.73）‎ ‎【分析】在直角三角形ADB中和直角三角形ACD中，根据锐角三角函数中的正切可以分别求得BD和CD的长，从而可以求得BC的长，本题得以解决．‎ ‎【解答】解：由题意可得，AD＝100米，∠ADC＝∠ADB＝90°，‎ ‎∴在Rt△ADB中，∠CAD＝30°，AD＝60米，‎ ‎∴tan∠CAD＝＝＝，‎ ‎∴CD＝20（米），‎ 在Rt△ADC中，∠DAB＝45°，AD＝60米，‎ ‎∴tan∠DAB＝＝1，‎ ‎∴BD＝60（米），‎ ‎∴BC＝BD+CD＝（60+20）≈95米，‎ 即这栋楼的高度BC是95米．‎ 31‎ ‎【点评】本题考查解直角三角形的应用﹣仰角俯角问题、锐角三角函数，解答此类问题的关键是明确题意，利用锐角三角函数解答．‎ ‎18．（8分）如图，一次函数y＝x+1的图象与反比例函数y＝的图象相交于A（2，m）和B两点．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）求点B的坐标．‎ ‎【分析】（1）将点A坐标代入一次函数解析式可求m的值，再将点A坐标代入反比例函数解析式，可求解；‎ ‎（2）联立方程组可求解．‎ ‎【解答】解：（1）∵一次函数y＝x+1的图象过点A（2，m），‎ ‎∴m＝×2+1＝2，‎ ‎∴点A（2，2），‎ ‎∵反比例函数y＝的图象经过点A（2，2），‎ ‎∴k＝2×2＝4，‎ ‎∴反比例函数的解析式为：y＝；‎ ‎（2）联立方程组可得：，‎ 31‎ 解得：或，‎ ‎∴点B（﹣4，﹣1）．‎ ‎【点评】本题考查了一次函数与反比例函数的交点问题，用待定系数法求反比例函数的解析式．本题难度适中．‎ ‎19．（10分）为了解同学们最喜欢一年四季中的哪个季节，数学社在全校随机抽取部分同学进行问卷调查，根据调查结果，得到如下两幅不完整的统计图．‎ 根据图中信息，解答下列问题：‎ ‎（1）此次调查一共随机抽取了　120　名同学；扇形统计图中，“春季”所对应的扇形的圆心角的度数为　108　；‎ ‎（2）若该学校有1500名同学，请估计该校最喜欢冬季的同学的人数；‎ ‎（3）现从最喜欢夏季的3名同学A，B，C中，随机选两名同学去参加学校组织的“我爱夏天”演讲比赛，请用列表或画树状图的方法求恰好选到A，B去参加比赛的概率．‎ ‎【分析】（1）由“夏季”的人数除以占的百分比得出调查学生的总数即可；求出“春季”的人数占的百分比，乘以360即可得到结果；‎ ‎（2）根据题意列式计算即可；‎ ‎（3）画树状图展示所有等可能的结果数，找出恰好选到A，B去参加比赛的的结果数，然后根据概率公式计算．‎ ‎【解答】解：（1）此次调查一共随机抽取了18÷15%＝120（名）同学；扇形统计图中，“春季”所对应的扇形的圆心角的度数为360°×＝108°，‎ 31‎ 故答案为：120，108；‎ ‎（2）1500×＝150（人），‎ 答：估计该校最喜欢冬季的同学的人数为150人；‎ ‎（3）画树状图为：‎ 共有6种等可能的结果数，其中恰好选到A，B去参加比赛的结果数为2，‎ 所以恰好选到A，B去参加比赛的概率＝＝．‎ ‎【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式计算事件A或事件B的概率．也考查了统计图．‎ ‎20．（10分）如图，AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．‎ ‎（1）求证：∠CAD＝∠CAB；‎ ‎（2）若＝，AC＝2，求CD的长．‎ ‎【分析】（1）连接OC，根据切线的性质，判断出AD∥OC，再应用平行线的性质，即可推得AC平分∠DAB；‎ 31‎ ‎（2）如图2，连接BC，设AD＝2x，AB＝3x，根据圆周角定理得到∠ACB＝∠ADC＝90°，根据相似三角形的性质即可得到结论．‎ ‎【解答】（1）证明：如图1，连接OC，‎ ‎，‎ ‎∵CD是切线，‎ ‎∴OC⊥CD．‎ ‎∵AD⊥CD，‎ ‎∴AD∥OC，‎ ‎∴∠1＝∠4．‎ ‎∵OA＝OC，‎ ‎∴∠2＝∠4，‎ ‎∴∠1＝∠2，‎ ‎∴AC平分∠DAB；‎ ‎（2）解：如图2，‎ 连接BC，‎ 31‎ ‎∵＝，‎ ‎∴设AD＝2x，AB＝3x，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ACB＝∠ADC＝90°，‎ ‎∵∠DAC＝∠CAB，‎ ‎∴△ACD∽△ABC，‎ ‎∴＝，‎ ‎∴＝，‎ ‎∴x＝2（负值舍去），‎ ‎∴AD＝4，‎ ‎∴CD＝＝2．‎ ‎【点评】此题主要考查了切线的性质和应用，相似三角形的判定和性质，以及平行线的性质和应用，要熟练掌握，解答此题的关键是要明确：若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．‎ 一、填空题（本大题共5个小题，每小题4分，共20分）‎ ‎21．（4分）在单词“mathematics”中任意选择一个字母，选到字母“a”的概率是　　．‎ ‎【分析】先数出“mathematics”中共多少个字母，让字母“a”的个数除以所有字母的总个数即为所求的概率．‎ ‎【解答】解：“mathematics”中共11个字母，其中共2个“a”，‎ 任意取出一个字母，有11种情况可能出现，‎ 取到字母“a”的可能性有两种，故其概率是；‎ 31‎ 故答案为 ‎【点评】本题考查概率的求法．用到的知识点为：概率＝所求情况数与总情况数之比．‎ ‎22．（4分）若m2﹣2m＝1，则代数式2m2﹣4m+3的值为　5　．‎ ‎【分析】原式变形后，把已知等式代入计算即可求出值．‎ ‎【解答】解：∵m2﹣2m＝1，‎ ‎∴原式＝2（m2﹣2m）+3＝2+3＝5．‎ 故答案为：5．‎ ‎【点评】此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．‎ ‎23．（4分）三角形的两边长分别为4和7，第三边的长是方程x2﹣8x+12＝0的解，则这个三角形的周长是　17　．‎ ‎【分析】先利用因式分解法解方程得到x1＝2，x2＝6，再根据三角形三边的关系得到三角形第三边长为3，然后计算三角形的周长．‎ ‎【解答】解：x2﹣8x+12＝0，‎ ‎（x﹣2）（x﹣6）＝0，‎ 解得：x1＝2，x2＝6，‎ 若x＝2，即第三边为2，4+2＝6＜7，不能构成三角形，舍去；‎ 当x＝6时，这个三角形周长为4+7+6＝17，‎ 故答案为：17．‎ ‎【点评】此题考查了解一元二次方程﹣因式分解法，以及三角形的三边关系，熟练掌握因式分解的方法是解本题的关键．‎ ‎24．（4分）如图，有一张长方形纸片ABCD，AB＝8cm，BC＝10cm，点E为CD上一点，将纸片沿AE折叠，BC的对应边B′C′恰好经过点D，则线段DE的长为　5　cm．‎ 31‎ ‎【分析】由折叠的性质可得AB＝AB'＝8cm，BC＝B'C'＝10cm，CE＝C'E，由勾股定理可求B'D的长，由勾股定理可求解．‎ ‎【解答】解：∵将纸片沿AE折叠，BC的对应边B′C′恰好经过点D，‎ ‎∴AB＝AB'＝8cm，BC＝B'C'＝10cm，CE＝C'E，‎ ‎∴B'D＝＝＝6cm，‎ ‎∴C'D＝B'C'﹣B'D＝4cm，‎ ‎∵DE2＝C'D2+C'E2，‎ ‎∴DE2＝16+（8﹣DE）2，‎ ‎∴DE＝5cm，‎ 故答案为5．‎ ‎【点评】本题考查了翻折变换，矩形的性质，勾股定理，熟练运用折叠的性质是本题的关键．‎ ‎25．（4分）如图，在平面直角坐标系xOy中，一次函数y＝x+1的图象与反比例函数y＝的图象交于A，B两点，若点P是第一象限内反比例函数图象上一点，且△ABP的面积是△AOB的面积的2倍，则点P的横坐标为　2或　．‎ 31‎ ‎【分析】分点P在AB下方、点P在AB上方两种情况，分别求解即可．‎ ‎【解答】解：①当点P在AB下方时 作AB的平行线l，使点O到直线AB和到直线l的距离相等，则△ABP的面积是△AOB的面积的2倍，‎ 直线AB与x轴交点的坐标为（﹣1，0），则直线l与x轴交点的坐标C（1，0），‎ 设直线l的表达式为：y＝x+b，将点C的坐标代入上式并解得：b＝﹣1，‎ 故直线l的表达式为y＝x﹣1①，而反比例函数的表达式为：y＝②，‎ 联立①②并解得：x＝2或﹣1（舍去）；‎ ‎②当点P在AB上方时，‎ 同理可得，直线l的函数表达式为：y＝x+3③，‎ 联立①③并解得：x＝（舍去负值）；‎ 故答案为：2或．‎ 31‎ ‎【点评】本题考查了反比例函数与一次函数的交点，当有两个函数的时候，着重使用一次函数，体现了方程思想，综合性较强．‎ 五、解答题（本大题共3个小题，共30分）‎ ‎26．（8分）某商品的进价为每件40元，在销售过程中发现，每周的销售量y（件）与销售单价x（元）之间的关系可以近似看作一次函数y＝kx+b，且当售价定为50元/件时，每周销售30件，当售价定为70元/件时，每周销售10件．‎ ‎（1）求k，b的值；‎ ‎（2）求销售该商品每周的利润w（元）与销售单价x（元）之间的函数解析式，并求出销售该商品每周可获得的最大利润．‎ ‎【分析】（1）利用待定系数法可求解析式；‎ ‎（2）由销售该商品每周的利润w＝销售单价×销售量，可求函数解析式，由二次函数的性质可求解．‎ ‎【解答】解：（1）由题意可得：，‎ ‎∴，‎ 答：k＝﹣1，b＝80；‎ ‎（2）∵w＝（x﹣40）y＝（x﹣40）（﹣x+80）＝﹣（x﹣60）2+400，‎ ‎∴当x＝60时，w有最大值为400元，‎ 答：销售该商品每周可获得的最大利润为400元．‎ ‎【点评】本题考查了二次函数的应用，待定系数法可求解析式，解答本题的关键是明确题意，利用函数和方程的思想解答．‎ ‎27．（10分）如图，Rt△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转得到△DEC，点D落在线段AB上，连接BE．‎ ‎（1）求证：DC平分∠ADE；‎ 31‎ ‎（2）试判断BE与AB的位置关系，并说明理由；‎ ‎（3）若BE＝BD，求tan∠ABC的值．‎ ‎【分析】（1）利用等腰三角形的性质以及旋转不变性解决问题即可．‎ ‎（2）结论：AB⊥BE．证明C，E，B，D四点共圆即可解决问题．‎ ‎（3）设BC交DE于O．连接AO．想办法证明△ACO是等腰直角三角形，OA＝OB即可解决问题．‎ ‎【解答】（1）证明：∵△DCE是由△ACB旋转得到，‎ ‎∴CA＝CD，∠A＝∠CDE ‎∴∠A＝∠CDA，‎ ‎∴∠CDA＝∠CDE，‎ ‎∴CD平分∠ADE．‎ ‎（2）解：结论：BE⊥AB．‎ 由旋转的性质可知，∠DBC＝∠CED，‎ ‎∴D，C，E，B四点共圆，‎ ‎∴∠DCE+∠DBE＝90°，‎ ‎∵∠DCE＝90°，‎ ‎∴∠DBE＝90°，‎ ‎∴BE⊥AB．‎ 31‎ ‎（3）如图，设BC交DE于O．连接AO．‎ ‎∵BD＝BE，∠DBE＝90°，‎ ‎∴∠DEB＝∠BDE＝45°，‎ ‎∵C，E，B，D四点共圆，‎ ‎∴∠DCO＝∠DEB＝45°，‎ ‎∵∠ACB＝90°，‎ ‎∴∠ACD＝∠OCD，‎ ‎∵CD＝CD，∠ADC＝∠ODC，‎ ‎∴△ACD∽△OCD（ASA），‎ ‎∴AC＝OC，‎ ‎∴∠AOC＝∠CAO＝45°，‎ ‎∵∠ADO＝135°，‎ ‎∴∠CAD＝∠ADC＝67.5°，‎ ‎∴∠ABC＝22.5°，‎ ‎∵∠AOC＝∠OAB+∠ABO，‎ ‎∴∠OAB＝∠ABO＝22.5°，‎ ‎∴OA＝OB，设AC＝OC＝m，则AO＝OB＝m，‎ ‎∴tan∠ABC＝＝＝﹣1．‎ 31‎ ‎【点评】本题属于三角形综合题，考查了旋转变换，全等三角形的判定和性质，等腰三角形的性质，四点共圆等知识，解题的关键是证明C，E，B，D四点共圆，属于中考压轴题．‎ ‎28．（12分）如图，在平面直角坐标系xOy中，直线y＝kx+3分别交x轴、y轴于A，B两点，经过A，B两点的抛物线y＝﹣x2+bx+c与x轴的正半轴相交于点C（1，0）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若P为线段AB上一点，∠APO＝∠ACB，求AP的长；‎ ‎（3）在（2）的条件下，设M是y轴上一点，试问：抛物线上是否存在点N，使得以A，P，M，N为顶点的四边形为平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．‎ ‎【分析】（1）利用待定系数法解决问题即可．‎ ‎（2）求出AB，OA，AC，利用相似三角形的性质求解即可．‎ ‎（3）分两种情形：①PA为平行四边形的边时，点M的横坐标可以为±2，求出点M的坐标即可解决问题．②当AP为平行四边形的对角线时，点M″的横坐标为﹣4，求出点M″的坐标即可解决问题．‎ ‎【解答】解：（1）由题意抛物线经过B（0，3），C（1，0），‎ 31‎ ‎∴，‎ 解得，‎ ‎∴抛物线的解析式为y＝﹣x2﹣2x+3‎ ‎（2）对于抛物线y＝﹣x2﹣2x+3，令y＝0，解得x＝﹣3或1，‎ ‎∴A（﹣3，0），‎ ‎∵B（0，3），C（1，0），‎ ‎∴OA＝OB＝3OC＝1，AB＝3，‎ ‎∵∠APO＝∠ACB，∠PAO＝∠CAB，‎ ‎∴△PAO∽△CAB，‎ ‎∴＝，‎ ‎∴＝，‎ ‎∴AP＝2．‎ ‎（3）由（2）可知，P（﹣1，2），AP＝2，‎ ‎①当AP为平行四边形的边时，点N的横坐标为2或﹣2，‎ ‎∴N（﹣2，3），N′（2，﹣5），‎ ‎②当AP为平行四边形的对角线时，点N″的横坐标为﹣4，‎ ‎∴N″（﹣4，﹣5），‎ 综上所述，满足条件的点N的坐标为（﹣2，3）或（2，﹣5）或（﹣4，﹣5）．‎ 31‎ ‎【点评】本题考查二次函数综合题，考查了待定系数法，相似三角形的判定和性质，平行四边形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．‎ 31‎