2018年湖南省株洲市中考数学试卷含答案

2018年湖南省株洲市中考数学试卷含答案

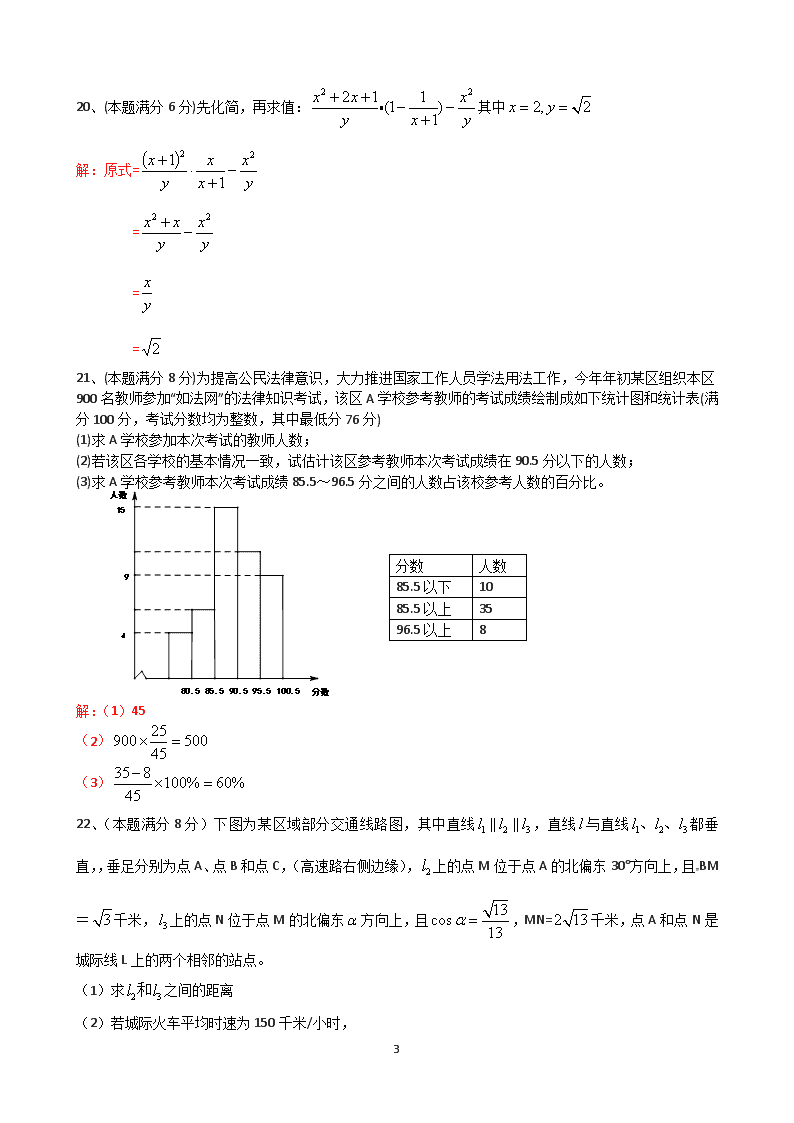
‎2018株洲市初中毕业学业考试数学试卷 一、选择题（每小题有且只有一个正确答案，本题共10小题，每小题3分，共30分）‎ ‎1、9的算术平方根是( A )‎ A、3　　　　　B、9　　　　　C、±3　　　　　D、±9‎ ‎2、下列运算正确的是( D )‎ A、　　　B、　　　C、　　　D、‎ ‎3、如图，的倒数在数轴上表示的点位于下列两个点之间( C )‎ A、点E和点F　　　B、点F和点G　　　C、点F和点G　　　　D、点G和点H ‎4、据资料显示，地球的海洋面积约为360000000平方千米，请用科学记数法表示地球海洋面积面积约为多少平方千米( B )‎ A、　　　　B、　　　C、　　　　D、‎ ‎5、关于的分式方程解为，则常数的值为( D )‎ A、　　　　　B、　　　　　C、　　　D、‎ ‎6、从这七个数中随机抽取一个数，恰好为负整数的概率为( A )‎ A、　　　　　　B、　　　　　　C、　　　　　　D、‎ ‎7、下列哪个选项中的不等式与不等式组成的不等式组的解集为.( C )‎ A、　　B、　　　　C、　　　D、‎ ‎8、已知二次函数的图像如下图，则下列哪个选项表示的点有可能在反比例函数的图象上( C )‎ A、（－1,2）　　　　B、（1，－2）　　　　C、（2,3）　　　D、（2，－3）‎ ‎9、如图，直线被直线所截，且，过上的点A作AB⊥交于点B，其中∠1＜30°，则下列一定正确的是( D )[来源:学§科§网Z§X§X§K]‎ A、∠2＞120°　　　　B、∠3＜60°　　　　C、∠4－∠3＞90°　　D、2∠3＞∠4‎ ‎10、已知一系列直线分别 7‎ 与直线相交于一系列点，设的横坐标为，则对于式子，下列一定正确的是( B )‎ A、大于1　　　B、大于0　　　　　C、小于－1　　　　D、小于0‎ 二、填空题（本题共8小题，每小题3分，共24分）‎ ‎11、单项式的次数　　3　　。‎ ‎12、睡眠是评价人类健康水平的一项重要指标，充足的睡眠是青少年健康成长的必要条件之一，小强同学通过问卷调查的方式了解到本班三位同学某天的睡眠时间分别为7.8小时，8.6小时，8.8小时，则这三位同学该天的平均睡眠时间是　　8.4　　。‎ ‎13、因式分解：＝　　　。‎ ‎14、如图，矩形ABCD的对角线AC与BD相交点O，AC＝10，P、Q分别为AO、AD的中点，则PQ的的长度为　2.5　　　。‎ ‎15、小强同学生日的月数减去日数为2，月数的两倍和日数相加为31，则小强同学生日的月数和日数的和为　20　‎ ‎16、如图，正五边形ABCDE和正三角形AMN都是⊙O的内接多边形，则∠BOM＝　48°　　。‎ ‎17、如图，O为坐标原点，△OAB是等腰直角三角形，∠OAB＝90°，点B的坐标为，将该三角形沿轴向右平移得到，此时点的坐标为，则线段OA在平移过程中扫过部分的图形面积为　4　。‎ ‎18、如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝　6　。‎ 三、解答题(本大题8小题，共66分)‎ ‎19、(本题满分6分)计算：‎ 解：原式=‎ ‎ =2-3‎ ‎ =-1‎ 7‎ ‎20、(本题满分6分)先化简，再求值：其中 解：原式=‎ ‎ =‎ ‎ =‎ ‎ =‎ ‎21、(本题满分8分)为提高公民法律意识，大力推进国家工作人员学法用法工作，今年年初某区组织本区900名教师参加“如法网”的法律知识考试，该区A学校参考教师的考试成绩绘制成如下统计图和统计表(满分100分，考试分数均为整数，其中最低分76分)‎ ‎(1)求A学校参加本次考试的教师人数；‎ ‎(2)若该区各学校的基本情况一致，试估计该区参考教师本次考试成绩在90.5分以下的人数；‎ ‎(3)求A学校参考教师本次考试成绩85.5～96.5分之间的人数占该校参考人数的百分比。‎ 分数 人数 ‎85.5以下 ‎10‎ ‎85.5以上 ‎35‎ ‎96.5以上 ‎8‎ 解：（1）45‎ （2） （3） ‎22、（本题满分8分）下图为某区域部分交通线路图，其中直线，直线与直线都垂直，，垂足分别为点A、点B和点C，（高速路右侧边缘），上的点M位于点A的北偏东30°方向上，且BM＝千米，上的点N位于点M的北偏东方向上，且，MN=千米，点A和点N是城际线L上的两个相邻的站点。‎ ‎（1）求之间的距离 ‎（2）若城际火车平均时速为150千米/小时，‎ 7‎ 求市民小强乘坐城际火车从站点 A到站点N需要多少小时？（结果用分数表示）‎ 解：（1）‎ （2） 过点M作MD⊥于点D.‎ ‎∵‎ ‎,(km）‎ ‎（小时）‎ ‎23、(本题满分8分)如图，在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD，其中AM=AN。‎ ‎(1)求证：Rt△ABM≌Rt△AND ‎(2)线段MN与线段AD相交于T，若AT=,求的值 解：第1问主要是读懂意思，‎ AD=AB，AM=AN，∠AMB＝∠AND=90°‎ 从而易证。Rt△ABM≌Rt△AND[来源:学,科,网Z,X,X,K]‎ ‎(2)由Rt△ABM≌Rt△AND易得：∠DAN＝∠BAM,DN=BM ‎∵∠AND=∠DAN+∠DAM= 90°；∠DAN+∠ADN= 90°‎ ‎∴∠DAM=∠AND ‎∴ND∥AM ‎∴△DNT∽△AMT ‎∴‎ ‎∵AT=　　∴‎ ‎∵Rt△ABM[来源:学_科_网Z_X_X_K]‎ ‎∴=‎ ‎24、(本题满分8分)，如图已知函数的图象与一次函数的图象相交不同的点A、B，过点A作AD⊥轴于点D，连接AO，其中点A的横坐标为，△AOD的面积为2。‎ ‎(1)求的值及=4时的值；‎ 7‎ ‎(2)记表示为不超过的最大整数，例如：，，设,若，求值 解：（1）k=4,‎ A(4,1), 1=4m+5, 解得m=-1‎ ‎（2）‎ 解得：‎ ‎25、(本题满分10分)如图，已知AB为⊙O的直径，AB=8，点C和点D是⊙O上关于直线AB对称的两个点，连接OC、AC，且∠BOC＜90°，直线BC和直线AD相交于点E，过点C作直线CG与线段AB的延长线相交于点F，与直线AD相交于点G，且∠GAF＝∠GCE ‎（1）求证：直线CG为⊙O的切线；‎ ‎（2）若点H为线段OB上一点，连接CH，满足CB＝CH，‎ ‎①△CBH∽△OBC ‎②求OH＋HC的最大值 （1） 证明：∵C、D关于AB对称 ‎ ∴∠GAF=∠CAF ‎∵∠GAF=∠GCE,∴∠GCE=∠CAF ‎∵OA=OC,∴∠CAF=∠ACO,∴∠GCE=∠ACO ‎∵AB为直径 ‎∴∠ACO+∠OCB=90°‎ ‎∴∠GCE+∠OCB=90°‎ 即∠OCG=90°，∴CG为圆O的切线.‎ （2） ‎①∵OC=OB,CH=BC 7‎ ‎∴∠OCB=∠OBC,∠CHB=∠CBH ‎∠CBH=∠OBC=∠OCB=∠CHB ‎△CBH∽△OBC ‎②‎ 设BC=x，则CH=x，BH=‎ ‎∴当x=2时，最大值为5.‎ ‎26、（本题满分12分）如图，已知二次函数的图象抛物线与轴相交于不同的两点，,且,‎ ‎(1)若抛物线的对称轴为求的值；‎ ‎（2）若，求的取值范围；‎ ‎（3）若该抛物线与轴相交于点D，连接BD，且∠OBD＝60°，抛物线的对称轴与轴相交点E，点F是直线上的一点，点F的纵坐标为，连接AF，满足∠ADB＝∠AFE，求该二次函数的解析式。‎ ‎ ‎ 解：（1），解得 ‎（2）由题意得二次函数解析式为：‎ ‎∵二次函数与x轴有两个交点 ‎∴‎ ‎∴‎ ‎∴‎ 7‎ （1） ‎∵，‎ 把带入中得：‎ ‎∴‎ 把带入中得：‎ ‎∴‎ ‎∴‎ ‎∵F的纵坐标为 ‎∴‎ 过点A作AG⊥DB于G.‎ 根据勾股定理可求出：‎ ‎∵‎ ‎∴△ADG∽△AFG ‎∴‎ ‎∴‎ ‎∴‎ ‎∴‎ 7‎