中考数学专题复习练习：整合拓展创新

中考数学专题复习练习：整合拓展创新

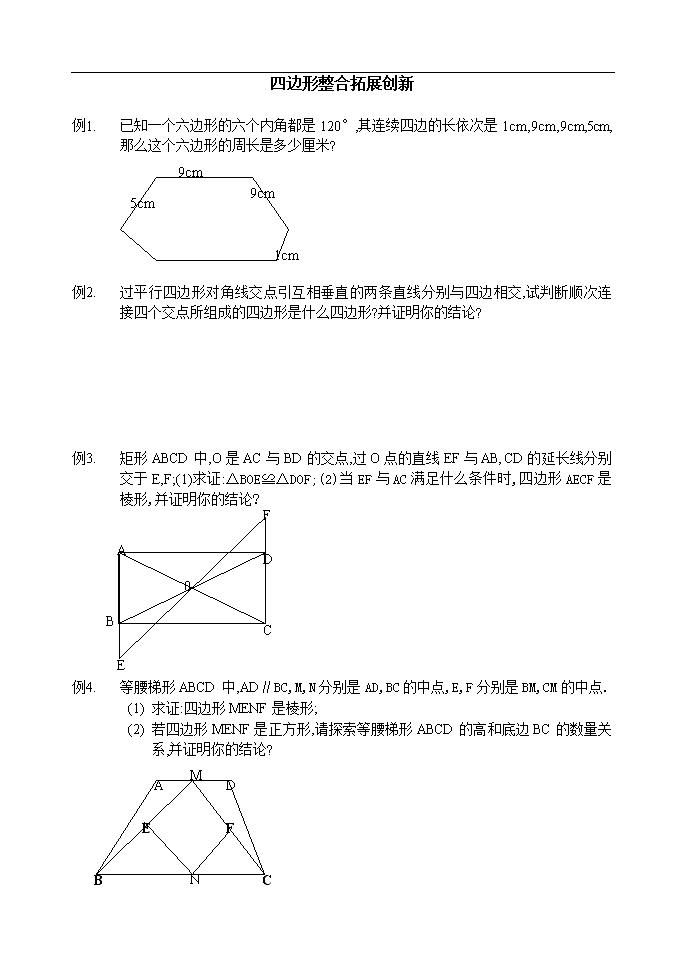
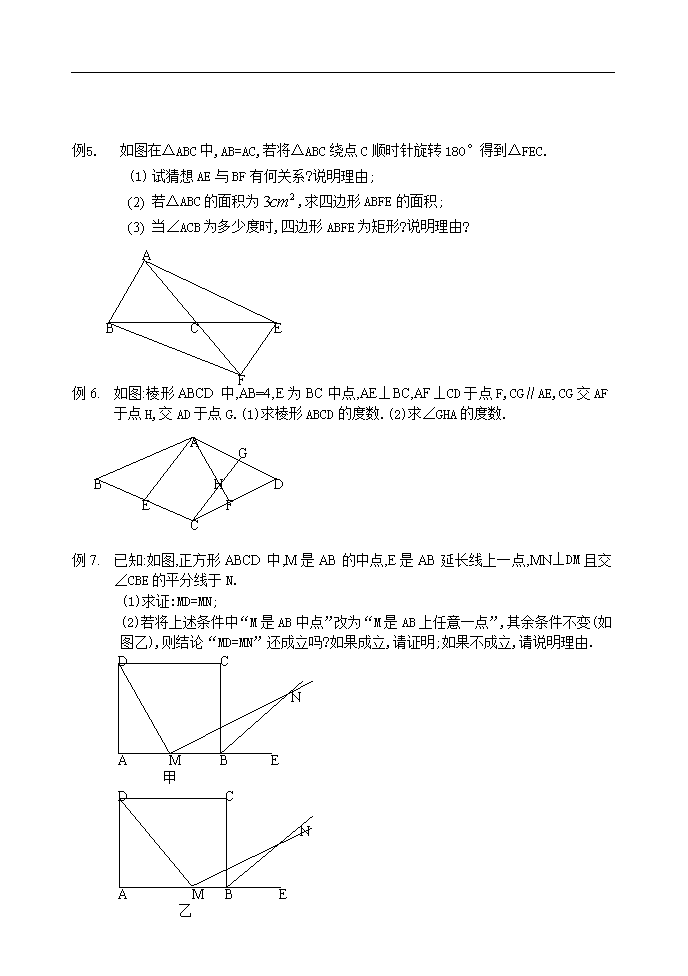
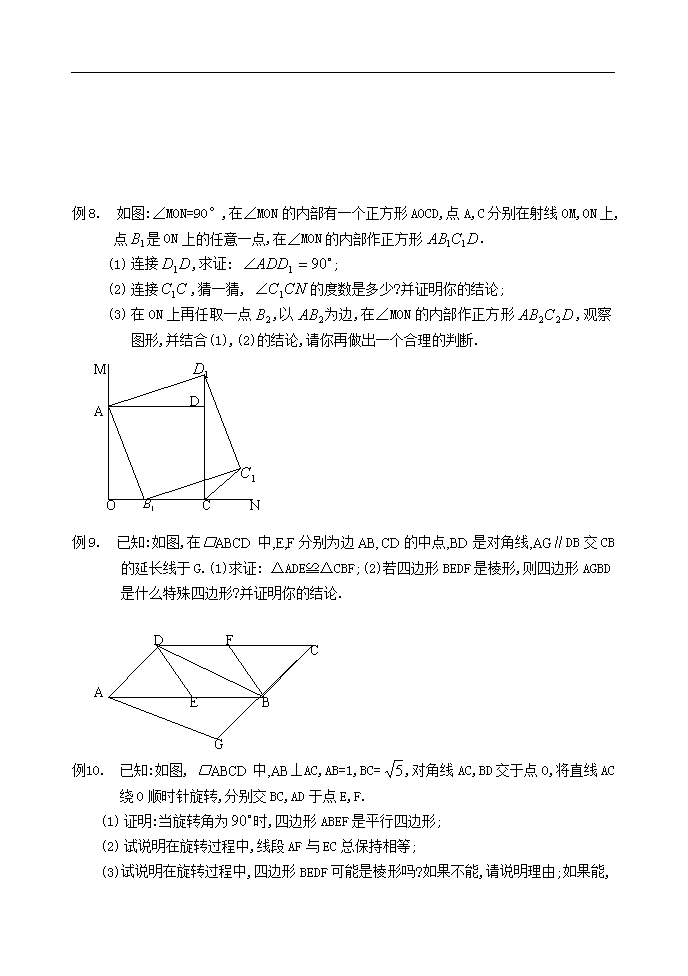
四边形整合拓展创新 例1. 已知一个六边形的六个内角都是120°,其连续四边的长依次是‎1cm,‎9cm,‎9cm,‎5cm,那么这个六边形的周长是多少厘米?‎ ‎1cm‎ ‎ ‎9cm‎ ‎ ‎9cm‎ ‎ ‎5cm‎ ‎ 例2. 过平行四边形对角线交点引互相垂直的两条直线分别与四边相交,试判断顺次连接四个交点所组成的四边形是什么四边形?并证明你的结论?‎ C ‎ DC ‎ EC ‎ BC ‎ FC ‎ ‎0C‎ ‎ AC ‎ 例3. 矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F;(1)求证:△BOE≌△DOF;(2)当EF与AC满足什么条件时,四边形AECF是棱形,并证明你的结论?‎ 例4. 等腰梯形ABCD中,AD∥BC,M,N分别是AD,BC的中点,E,F分别是BM,CM的中点.‎ (1) 求证:四边形MENF是棱形;‎ (2) 若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系,并证明你的结论?‎ C ‎ FC ‎ EC ‎ BC ‎ DC ‎ AC ‎ NC ‎ MC ‎ 例1. 如图在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.‎ (1) 试猜想AE与BF有何关系?说明理由;‎ (2) 若△ABC的面积为,求四边形ABFE的面积;‎ (3) 当∠ACB为多少度时,四边形ABFE为矩形?说明理由?‎ F ‎ E ‎ C ‎ B ‎ A ‎ 例6. 如图:棱形ABCD中,AB=4,E为BC中点,AE⊥BC,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.(1)求棱形ABCD的度数.(2)求∠GHA的度数.‎ C ‎ FC ‎ DC ‎ EC ‎ BC ‎ AC ‎ GC ‎ HC ‎ 例7. 已知:如图,正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM且交 ∠CBE的平分线于N.‎ ‎(1)求证:MD=MN;‎ D ‎ A ‎ MA ‎ BA ‎ CA ‎ EA ‎ NA ‎ 甲 ‎ ‎(2)若将上述条件中“M是AB中点”改为“M是AB上任意一点”,其余条件不变(如图乙),则结论“MD=MN”还成立吗?如果成立,请证明;如果不成立,请说明理由.‎ D ‎ A ‎ MA ‎ BA ‎ CA ‎ EA ‎ NA ‎ 乙 ‎ 例8. 如图:∠MON=90°,在∠MON的内部有一个正方形AOCD,点A,C分别在射线OM,ON上,点是ON上的任意一点,在∠MON的内部作正方形.‎ (1) 连接,求证: ;‎ (2) 连接,猜一猜, 的度数是多少?并证明你的结论;‎ M ‎ AM ‎ OM‎ ‎ DM ‎ CM ‎ NM ‎ ‎ ‎ ‎ ‎ ‎ ‎ (3) 在ON上再任取一点,以为边,在∠MON的内部作正方形,观察图形,并结合(1),(2)的结论,请你再做出一个合理的判断.‎ 例9. 已知:如图,在□ABCD中,E,F分别为边AB,CD的中点,BD是对角线,AG∥DB交CB的延长线于G.(1)求证: △ADE≌△CBF;(2)若四边形BEDF是棱形,则四边形AGBD是什么特殊四边形?并证明你的结论.‎ AS G ‎ BG ‎ CG ‎ FG ‎ EG ‎ DG ‎ ‎ ‎ 例10. 已知:如图, □ABCD中,AB⊥AC,AB=1,BC=,对角线AC,BD交于点0,将直线AC绕0顺时针旋转,分别交BC,AD于点E,F.‎ (1) 证明:当旋转角为时,四边形ABEF是平行四边形;‎ (2) 试说明在旋转过程中,线段AF与EC总保持相等;‎ ‎(3)‎ 试说明在旋转过程中,四边形BEDF可能是棱形吗?如果不能,请说明理由;如果能,说明理由.并求出此时AC绕点O顺时针旋转的度数.‎A ‎ BA ‎ FA ‎ EA ‎ DA ‎ CDA ‎ ODA ‎