四川省内江市2017年中考数学试题

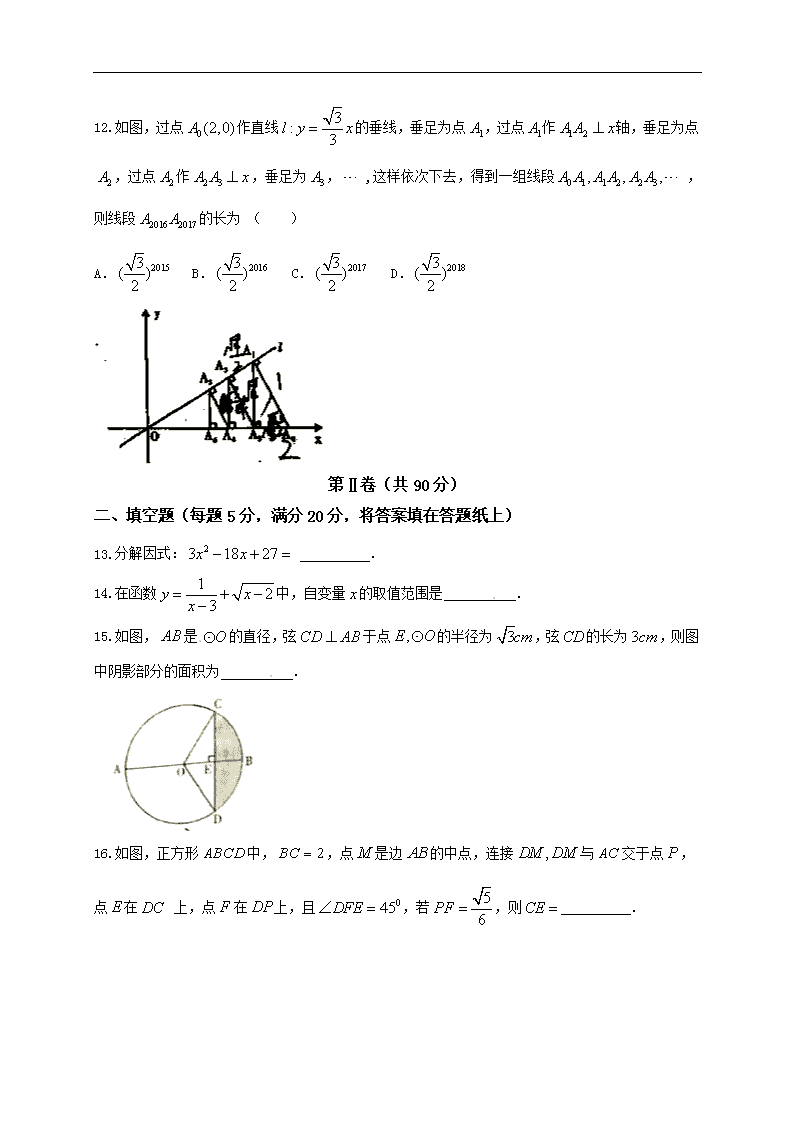
四川省内江市2017年中考数学试题

内江市2017年初中学业水平考试高中阶段学校招生考试试卷 数学 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.下面四个数中比小的数是（ ） ‎ A． B． C． D． ‎ ‎2. 是指大气中直径小于或定于的颗粒物，也称为可入肺颗粒物，它们含有一定量的有毒、有害物质，对人体健康和大气环境质量有恒大的影响，用科学计数法可表示为（ ）‎ A． B． C． D．‎ ‎3. 为了解某市老人的身体健康状况，需要抽取部分老人进行调查，下列抽取老人的方法最合适的是（ ）‎ A．随机抽取为女性老人 B．随机抽取为男性老人 ‎ C．随机抽取公园内为老人 D．在城市和乡镇选个点，每个任选为老人 ‎4. 如图，直线，直角三角形的顶点在直线上，则的余角等于（ ）‎ A． B． C． D．‎ ‎5.由一些大小相同的小正方体搭成的几何体的俯视图如下图所示，其中正方形总的数字表示该位置上的小正方体的个数，那么该几何体的主视图是 （ ）‎ ‎6. 下列图形中：平行四边形、矩形、菱形、圆、等腰三角形，这些图形总只是轴对称图形的有（ ）‎ A．1个 B．2个 C．3个 D．4个 ‎7. 某中学对该校九年级名女学生进行一次立定跳远测试，成绩如下表：‎ 这些立定跳远成绩的中位数和众数分别是（ ）‎ A． B． C． D． ‎ ‎8.下列计算正确的是 （ ）‎ A． B． C． D． ‎ ‎9. 端午节前夕，某超市用元购进两种共件，其中型商品每件元，型商品每件元，设购买型商品件，型商品件，依题意列出方程组正确的是（ ）‎ A． B． C． D． ‎ ‎10. 不等式组 的非负整数解的个数是（ ）‎ A． B． C． D． ‎ ‎11.如图，在矩形中，为坐标原点，分别在轴、轴上，点的坐标为， 将沿所在直线对折后，点落在 处，则点的坐标为 （ ）‎ A． B． C． D．‎ ‎12.如图，过点作直线的垂线，垂足为点，过点作轴，垂足为点，过点作，垂足为， ,这样依次下去，得到一组线段 ，则线段的长为 （ ）‎ A． B． C． D． ‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.分解因式： ．‎ ‎14.在函数中，自变量的取值范围是 ．‎ ‎15.如图，是的直径，弦于点的半径为，弦的长为，则图中阴影部分的面积为 ．‎ ‎16.如图，正方形中，，点是边的中点，连接与交于点，点在 上，点在上，且，若，则 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 计算： ‎ ‎18. 如图，平分，垂足为点，求证：是等腰三角形.‎ ‎19.小明随机调查了若干市民租用共享单车的骑车时间 （单位：分），将获得的数据分成四组，绘制了如下统计图（），根据图总信息，解答下列问题：‎ ‎（1）这项被调查的总人数是多少人？‎ ‎（2）使求表示组的扇形统计图的圆心角的度数，补全条形统计图；‎ ‎（3）如果小明向从组的甲乙丙丁死人中随机选择两人了解平时租用共享单车情况，请用列表或画树状图的方法求出恰好选中甲的概率.‎ ‎20.如图，某人为了测量小山顶的塔的高，他在山下的点处测得塔尖点的仰角为，在沿方向前进到达山脚点，测得塔尖点的仰角为，塔底点 的仰角为，求塔的高度（结果保留根号）‎ ‎21. 已知两点是一次函数和反比例函数图象的两个交点.‎ ‎（1）求一次函数和反比例函数的解析式；‎ ‎（2）求的面积；‎ ‎（3）观察图象，直接写出不等式的解集.‎ B卷（共60分）‎ ‎22.若实数 满足，则 ‎ ‎23.如图，四边形中，,是的平分线，且为垂足，，若四边形的面积为 ，则四边形的面积是 ‎[来源:学&科&网Z&X&X&K]‎ ‎24. 设是方程的两实数根，则 ‎ ‎25.如图，已知直线之间的距离为8，点到直线的距离为6，点到直线点距离为4，，在直线上有一动点，直线上有一动点，满足，且最小，‎ 此时 ‎ 五、解答题（本大题共3小题，每小题12分，共36分）‎ ‎26.观察下列等式：‎ 第一个等式：；‎ 第二个等式：；‎ 第三个等式：；‎ 第四个等式：，‎ 按上述规律，回答下列问题：‎ ‎（1）请写出第六个等式： ‎ ‎（2）用含的代数式表示第个等式 ‎ ‎（3） （得出最简结果）[来源:学科网]‎ ‎（4）计算：‎ ‎27.如图，在中，直径垂直于不过圆心的弦，垂足为点，连接，点在上，且.‎ ‎（1）求证：‎ ‎（2）过点作的切线交的延长线于点，试判断与是否相等，并说明理由；‎ ‎（3）设半径为，点为中点，点在上，求线段的最小值.‎ ‎28.如图，在平面直角坐标系中，抛物线与轴交于点，与轴交于两点 ，点坐标为，抛物线的对称轴方程为.‎ ‎（1）求抛物线的解析式；‎ ‎（2）点从点出发，在线段上以每秒3个单位长度的速度项点运动，同时点从点出发，在线段上以每秒1个单位长度的速度向点运动，其中一个点到到终点时，另一个点也停止运动，设的面积为，点运动时间为，试求与的函数关系，并求的最大值；‎ ‎（3）在点运动过程中，是否存在某一时刻，使为直角三角形？若存在，求出值；若不存在，请说明理由.‎ 四川省内江市2017年中考数学试题答案 ‎1-5 DCDBA 6-10ACCBB 11‎‎-12AC ‎13.‎ ‎14.且 ‎15.‎ ‎16. 分析：以点为原点，直线分别为轴，建立直角坐标系，可分别求出直线的方程，求得交点．利用两点间的距离公式得到，故．再证明与相似，所以根据，得到，故求出．‎ ‎17.8[来源:学科网]‎ ‎18.证明：依题可知：为的平分线，故，又因为，所以，因为，且，故有，因此是等腰三角形.‎ ‎19.（1）（人）；（2）；（3）‎ ‎20.分析：令，因此，借助三角函数可得：，可得到，解出，所以，且，所以塔高．‎ ‎21.（1）反比例函数：； 一次函数：；‎ ‎（2）求出，；‎ ‎（3）取值范围：或者；‎ ‎22.；分析：由式子知：，则有：‎ ‎23. 分析：延长直线交于点，因为垂直且平分，所以为等腰三角形．由于，故为中点，所以根据面积比等于相似比的平方，有：，所以，令，则，解出，故本题面积是1．‎ ‎24. 5 分析：先通分，再使用公式法和韦达定理即可.‎ ‎25.分析：如图所示：，且，所以满足：‎ 故有．‎ 26. ‎（1）；‎ （2） ‎；‎ （3） ‎；‎ （4） ‎27.‎ 分析：‎ ‎（1）连接，因为，所以，由于垂直且平分，所以是等腰三角形，即，因此，故．根据相似三角形的性质可得：，所以：．‎ ‎（2）连接，则，又因为，且，所以，故；‎ ‎（3）连接，交圆于点，此时最小.因为是中点，可得出是等边三角形，所以，且，根据三角函数知，借助勾股定理可得，因此，‎ ‎[来源:学科网ZXXK]‎ ‎[来源:Z§xx§k.Com]‎ ‎28.（1）根据二次函数的对称性得到，设方程为，代入点，求得方程为；‎ ‎（2）设运动时间为，那么可以得到，又因为，则有，故，所以当时，三角形的面积最大为；‎ （3） ‎①若时：有，解出；‎ ‎②若时：不满足条件，应该舍去；‎ ‎③若时：有，且由（2）知道，解出；‎