2020九年级数学下册 第二十六章专题训练（一）反比例函数系数k的两个几何模型同步练习

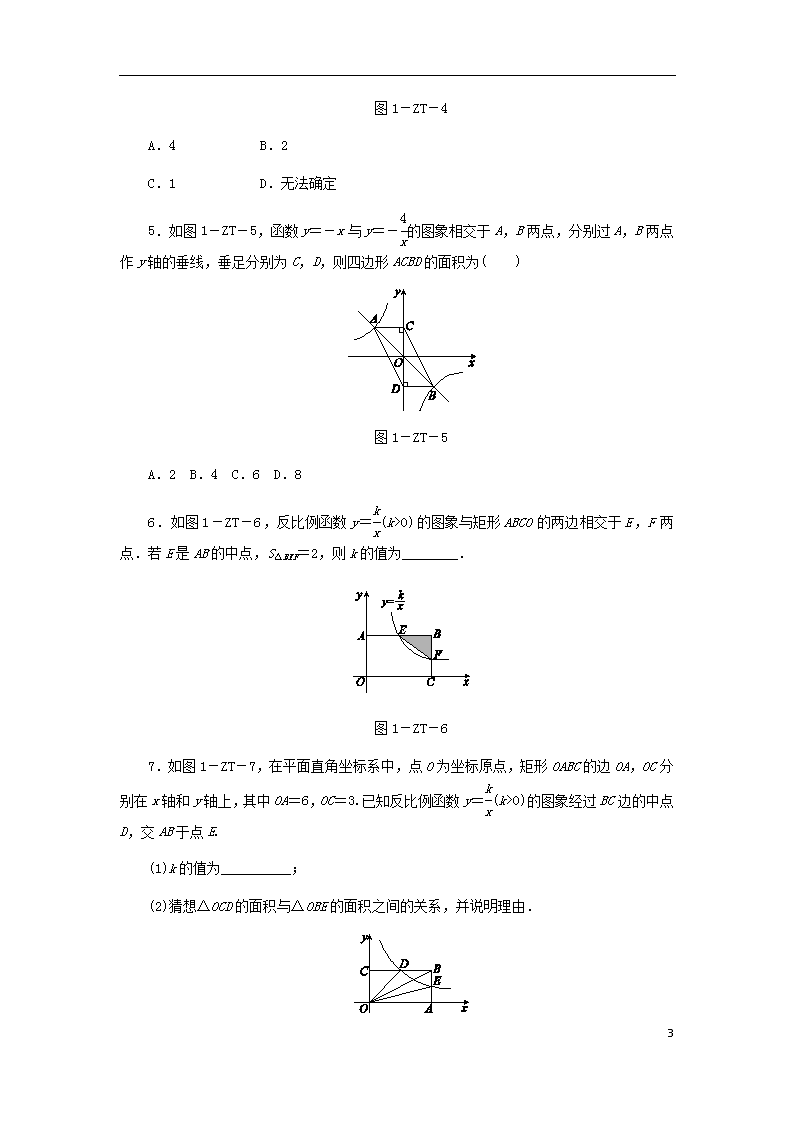
2020九年级数学下册 第二十六章专题训练（一）反比例函数系数k的两个几何模型同步练习

专题训练(一)　反比例函数系数k的两个几何模型 ‎►　模型一　k与三角形的面积 ‎1．如图1－ZT－1，分别过反比例函数y＝(x＞0)的图象上任意两点A，B作x轴的垂线，垂足分别为C，D，连接OA，OB，设△AOC和△BOD的面积分别是S1，S2，比较它们的大小，可得(　　)‎ 图1－ZT－1‎ A．S1＞S2 B．S1＝S2‎ C．S1＜S2 D．大小关系不能确定 ‎2．如图1－ZT－2，在平面直角坐标系中，A是函数y＝(x＜0)图象上的点，过点A作y轴的垂线交y轴于点B，点C在x轴上．若△ABC的面积为1，则k的值为________．‎ 6‎ 图1－ZT－2‎ ‎3．2017·湖州如图1－ZT－3，在平面直角坐标系xOy中，已知直线y＝kx(k＞0)分别交反比例函数y＝和y＝在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交y＝的图象于点C，连接AC.若△ABC是等腰三角形，则k的值是__________．‎ 图1－ZT－3‎ ‎►　模型二　k与四边形的面积 过反比例函数图象上的任意一点P分别作x轴、y轴的垂线，则可得两条垂线与x轴、y轴围成的矩形的面积等于|k|.反之根据矩形的面积结合图象所在象限可求得k的值．‎ ‎　　　‎ ‎4．如图1－ZT－4，A，B两点在双曲线y＝上，分别过A，B两点向坐标轴作垂线段，已知S1＋S2＝6，则S阴影＝(　　)‎ 6‎ 图1－ZT－4‎ A．4 B．2 ‎ C．1 D．无法确定 ‎5．如图1－ZT－5，函数y＝－x与y＝－的图象相交于A，B两点，分别过A，B两点作y轴的垂线，垂足分别为C，D，则四边形ACBD的面积为(　　)‎ 图1－ZT－5‎ A．2 B．‎4 C．6 D．8‎ ‎6．如图1－ZT－6，反比例函数y＝(k>0)的图象与矩形ABCO的两边相交于E，F两点．若E是AB的中点，S△BEF＝2，则k的值为________．‎ 图1－ZT－6‎ ‎7．如图1－ZT－7，在平面直角坐标系中，点O为坐标原点，矩形OABC的边OA，OC分别在x轴和y轴上，其中OA＝6，OC＝3.已知反比例函数y＝(k>0)的图象经过BC边的中点D，交AB于点E.‎ ‎(1)k的值为__________；‎ ‎(2)猜想△OCD的面积与△OBE的面积之间的关系，并说明理由．‎ 6‎ 图1－ZT－7‎ 6‎ 详解详析 ‎1．[解析] B　根据k的几何意义，得S1＝S2＝.‎ ‎2．[答案] －2‎ ‎[解析] ∵AB⊥y轴，∴AB∥CO，‎ ‎∴△AOB的面积＝AB·OB.‎ ‎∵S△ABC＝AB·OB＝1，∴|k|＝2.‎ ‎∵k＜0，∴k＝－2.‎ ‎3．[答案] 或 ‎[解析] ∵点B是函数y＝kx和y＝的图象的交点，由y＝kx＝，解得x＝(负值已舍去)，则y＝3 ，‎ ‎∴点B的坐标为(，3 )．‎ ‎∵点A是函数y＝kx和y＝的图象的交点，由y＝kx＝，解得x＝(负值已舍去)，‎ 则y＝，∴点A的坐标为(，)．‎ ‎∵BD⊥x轴，‎ ‎∴点C的横坐标为，纵坐标为＝，‎ ‎∴点C的坐标为(，)，∴BA≠AC.‎ 若△ABC是等腰三角形，则分以下两种情况讨论：‎ ‎①BA＝BC，则＝3 －，解得k＝(负值已舍去)；‎ 6‎ ‎②AC＝BC，则＝3 －，解得k＝(负值已舍去)．‎ 综上所述，当△ABC是等腰三角形时，k＝或.‎ ‎4．[解析] C　根据题意，得S1＋S阴影＝S2＋S阴影＝4，所以S1＝S2，而S1＋S2＝6，所以S1＝S2＝3，所以S阴影＝4－3＝1.‎ ‎5．D ‎6．[答案] 8‎ ‎[解析] 设E，则点B的纵坐标也为.‎ 因为E是AB的中点，所以点F的横坐标为2a，代入y＝得到点F的纵坐标为，‎ 所以BF＝－＝，‎ 所以S△BEF＝2＝··a＝，解得k＝8.‎ ‎7．解：(1)由题意可得C(0，3)，B(6，3)，‎ 则BC的中点D的坐标为(3，3)．‎ ‎∵函数y＝的图象经过点D，∴k＝9.‎ ‎(2)相等．理由如下：‎ 对于y＝，令x＝6，则y＝，‎ ‎∴E，即AE＝，‎ ‎∴BE＝AB－AE＝，‎ ‎∴S△OBE＝BE·OA＝××6＝.‎ 又∵S△OCD＝CD·OC＝×3×3＝，‎ ‎∴S△OBE＝S△OCD.‎ 6‎