八年级下册数学同步练习第1章复习2 湘教版

八年级下册数学同步练习第1章复习2 湘教版

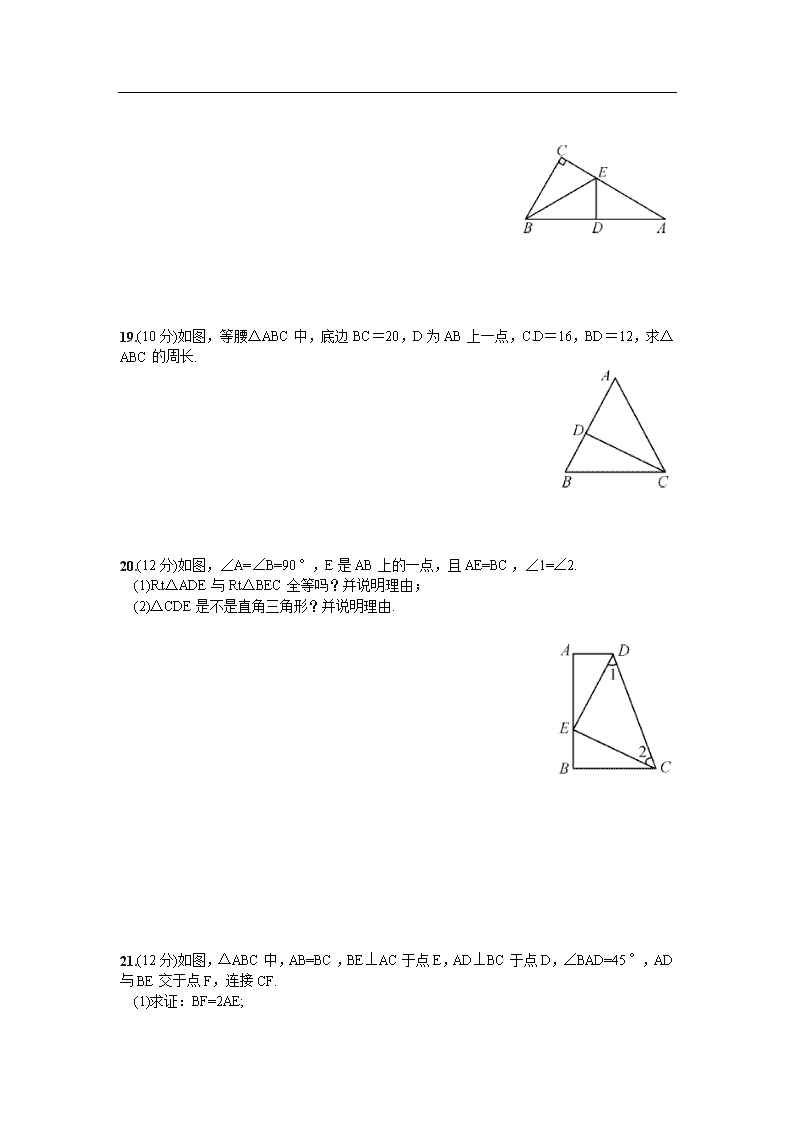
‎《直角三角形》复习 一、选择题(每小题3分,共30分)‎ ‎1.如图，∠BAC=90°，AD⊥BC，则图中互余的角有( )‎ ‎ A.2对 B.3对 C.4对 D.5对 ‎ [来源:学。科。网]‎ ‎ 第1题图 第3题图 第6题图 ‎2.在直角△ABC中，∠C=30°，斜边AC的长为5 cm，则AB的长为( )‎ ‎ A.2 cm B.2.5 cm C.3 cm D.4 cm ‎3.如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，已知BC=8，AC=6，则斜边AB上的高是( )‎ ‎ A.10 B.5 C. D.‎ ‎4.直角三角形斜边上的中线长是6.5，一条直角边是5，则另一直角边长等于( )[来源:Zxxk.Com]‎ ‎ A.13 B.12 C.10 D.5‎ ‎5.在下列选项中，以线段a，b，c的长为边，能构成直角三角形的是( )‎ ‎ A.a=3，b=4，c=6 B.a=5，b=6，c=7‎ ‎ C.a=6，b=8，c=9 D.a=7，b=24，c=25‎ ‎6.如图，在四边形ABCD中，AD=CB，DE⊥AC于点E，BF⊥AC于点F，且DE=BF，则图中全等三角形有( )‎ ‎ A.1对 B.2对 C.3对 D.4对 ‎7.△ABC中，∠A∶∠B∶∠C=1∶2∶3，则BC∶AB=( )‎ ‎ A.1∶1 B.1∶2 C.1∶3 D.2∶3‎ ‎8.如图，在△ABC中，AD是△ABC中∠BAC的平分线，且BD＞DC，则下列说法中正确的是( )‎ ‎ A.点D到AB边的距离大于点D到AC边的距离 ‎ B.点D到AB边的距离等于点D到AC边的距离 ‎ C.点D到AB边的距离小于点D到AC边的距离 ‎ D.点D到AB边的距离与点D到AC边的距离大小关系不确定 ‎ [来源:学科网]‎ 第8题图 第10题图 ‎9.等腰三角形的一腰长为3a，底角为15°，则另一腰上的高为( )‎ ‎ A.a B.a C.2a D.3a ‎10.如图，已知点P到AE,AD,BC的距离相等，下列说法：①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上；④点P在∠BAC，∠CBE，∠BCD的平分线的交点上.其中正确的是( )‎ ‎ A.①②③④ B.①②③ C.④ D.②③‎ 二、填空题(每小题3分,共18分)‎ ‎11.若直角三角形的一个锐角为50°，则另一个锐角的度数是__________.‎ ‎12.在Rt△ABC中，∠C=90°，∠B=2∠A，BC=3 cm，AB=__________cm.‎ ‎13.已知,在Rt△ABC中，∠ACB=90°，CD⊥AB于D，且AD=3，AC=6.则AB=__________.‎ ‎14.如图，在△ABC中，CF⊥AB于点F，BE⊥AC于点E，M为BC的中点，EF=4，BC=6，则△EFM的周长是__________.‎ ‎ ‎ 第14题图 第16题图 ‎15.生活经验表明：靠墙摆放梯子时，若梯子底端离墙约为梯子长度的时，则梯子比较稳定.现有一长度为9 m的梯子，当梯子稳定摆放时，它的顶端能到达8.5 m高的墙头吗？__________(填“能”或“不能”).‎ ‎16.如图，每个小正方形的边长均为1，△ABC的三边长分别为a，b，c；则a，b，c的大小关系是__________.‎ 三、解答题(共52分)‎ ‎17.(8分)已知Rt△ABC中，其中两边的长分别是3，5，求第三边的长.‎ ‎18.(10分)如图，在Rt△ACB中，∠C=90°，BE平分∠ABC，ED垂直平分AB于点D，若AC=9，求AE的长.‎ ‎19.(10分)如图，等腰△ABC中，底边BC＝20，D为AB上一点，CD＝16，BD＝12，求△ABC的周长.‎ ‎20.(12分)如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2.‎ ‎ (1)Rt△ADE与Rt△BEC全等吗？并说明理由；‎ ‎ (2)△CDE是不是直角三角形？并说明理由.‎ ‎21.(12分)如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF.‎ ‎ (1)求证：BF=2AE;‎ ‎ (2)若CD=，求AD的长.‎ ‎[来源:学科网]‎ 参考答案 ‎1.C 2.B 3.C 4.B 5.D 6.C 7.B 8.B 9.B 10.A ‎11.40° 12.6 13.12 14.10 15.不能 16.c＜a＜b ‎17.当已知两条边是直角边时，由勾股定理得第三条边的长为=；‎ ‎ 当已知两条边中有一条是直角边而另一条是斜边时，第三边长为=4.‎ ‎ ∴第三边的长为或4.‎ ‎18.设AE＝x，则CE＝9-x.‎ ‎ ∵BE平分∠ABC，CE⊥CB，ED⊥AB，‎ ‎ ∴DE＝CE＝9-x.‎ ‎ 又∵ED垂直平分AB，‎ ‎ ∴AE＝BE，∠A＝∠ABE＝∠CBE.‎ ‎ ∵在Rt△ACB中，∠A+∠ABC＝90°，‎ ‎ ∴∠A＝∠ABE＝∠CBE＝30°.‎ ‎ ∴DE＝AE.‎ ‎ 即9-x＝x.解得x＝6.‎ ‎ 即AE的长为6.‎ ‎19.设AD=x，AC=AB=12+x.‎ ‎ ∵BC＝20，CD＝16，BD＝12，‎ ‎ ∴BC2＝CD2+BD2.‎ ‎ ∴△BDC是直角三角形.‎ ‎ ∴∠BDC=∠ADC=90°.‎ ‎ 在Rt△ACD中，AD2+CD2=AC2.‎ ‎ ∴x2+162=(12+x)2.∴x=.‎ ‎ ∴△ABC的周长为：2AB+BC=2×(12+)+20=53.‎ ‎20.(1)Rt△ADE与Rt△BEC全等.‎ 理由：∵∠1=∠2，∴DE=CE.‎ ‎∵∠A=∠B=90°，AE=BC，‎ ‎∴Rt△ADE≌Rt△BEC（HL）.‎ ‎ (2)△CDE是直角三角形.[来源:学&科&网Z&X&X&K]‎ 理由：∵Rt△ADE≌Rt△BEC，‎ ‎∴∠ADE=∠BEC.‎ ‎∵∠ADE+∠AED=90°，‎ ‎∴∠BEC+∠AED=90°.‎ ‎∴∠DEC=90°.‎ ‎∴△CDE是直角三角形.‎ ‎21.(1)证明：∵AD⊥BC，∠BAD=45°，‎ ‎∴∠ABD=∠BAD=45°.‎ ‎∴AD=BD.‎ ‎∵AD⊥BC，BE⊥AC，‎ ‎∴∠CAD+∠ACD=90°，∠CBE+∠ACD=90°.‎ ‎∴∠CAD=∠CBE.‎ 又∵∠CDA=∠BDF=90°，‎ ‎∴△ADC≌△BDF(ASA).‎ ‎∴AC=BF.‎ ‎∵AB=BC，BE⊥AC，‎ ‎∴AE=EC，即AC=2AE，‎ ‎∴BF=2AE;‎ ‎ (2)∵△ADC≌△BDF，‎ ‎∴DF=CD=.‎ ‎∴在Rt△CDF中，CF==2.‎ ‎∵BE⊥AC，AE=EC，‎ ‎∴AF=FC=2，‎ ‎∴AD=AF+DF=2+.‎