- 2021-11-01 发布 |
- 37.5 KB |
- 10页

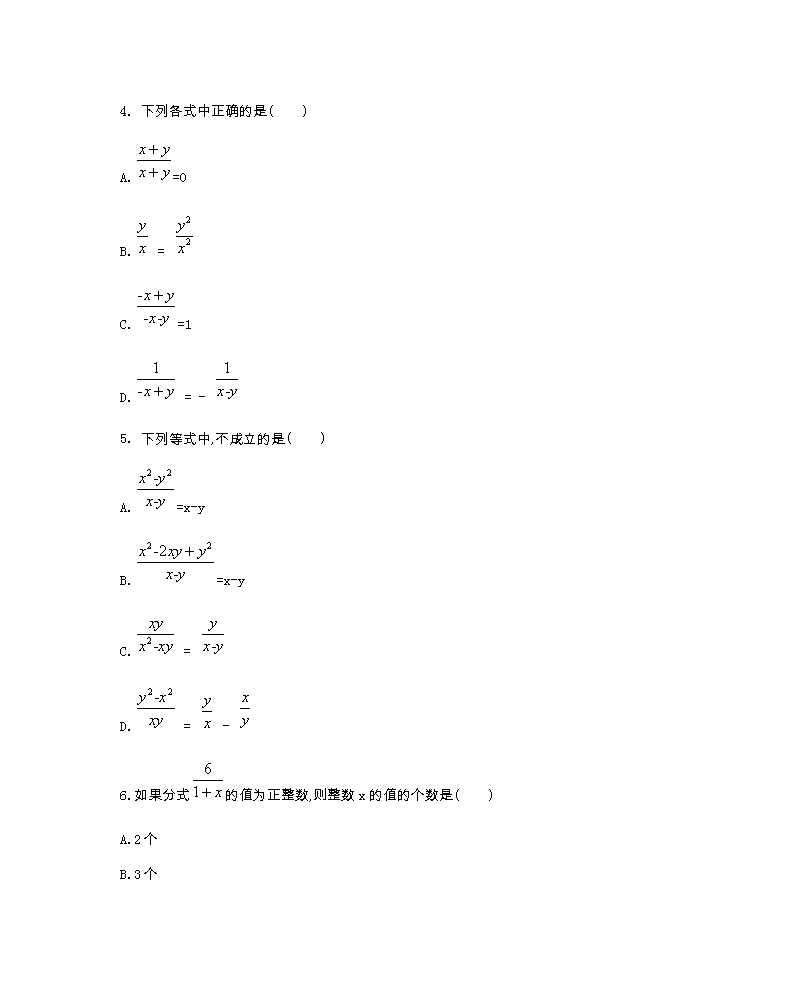

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版八年级数学(下册)第五章测试卷(附答案)
北师八下数学测试卷第五章 1. 使分式有意义的x的取值范围是( ) A.x=2 B.x≠2 C.x=-2 D.x≠-2 2. 已知两个分式:A=,B= + ,其中x≠±2,则A与B 的关系是( ) A.相等 B.互为倒数 C.互为相反数 D.A大于B 3. 下列各式从左到右变形正确的是( ) A. + =3(x+1)+2y B. = C. = D. = 4. 下列各式中正确的是( ) A.=0 B. = C.=1 D. = - 5. 下列等式中,不成立的是( ) A.=x-y B.=x-y C. = D. = - 6.如果分式的值为正整数,则整数x的值的个数是( ) A.2个 B.3个 C.4个 D.5个 7.把a千克盐溶于b千克水中,得到一种盐水,若有这种盐水x千克,则其中含盐( ) A.千克 B.千克 C.千克 D.千克 8 .把分式方程 - =1的两边同时乘以x-2,约去分母,得( ) A.1-(1-x)=1 B.1+(1-x)=1 C.1-(1-x)=x-2 D.1+(1-x)=x-2 9.化简: ÷ ·的结果是 . 10.计算:x· ÷ ·y= . 11.已知当x=-2时,分式无意义,x=4时,此分式的值为0,则a+b= . 12.一项工程,甲单独做x小时完成,乙单独做y小时完成,则两人一起完成这项工程需要 小时. 13.已知 - = ,则的值是 . 14.若 - =0无解,则m的值是 . 15.解答题. (1)约分:① ② (2)通分:① ,,- ② ,, 16.(1)要使分式的值为零,x和y的取值范围是什么? (2)已知: + = ,求 + 的值. 17. 解方程. (1) = (2) + =1 18.解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等. (1)设A= - ,B=,求A与B的积; (2)提出(1)的一个“逆向”问题,并解答这个问题. 19.A,B两地相距80千米,一辆公共汽车从A地出发开往B地,2小时后,又从A地开来一辆小汽车,小汽车的速度是公共汽车的3倍.结果小汽车比公共汽车早40分钟到达B地.求两种车的速度. 20.关于x的方程:x+ =c + 的解是x1=c,x2=; x- = c- (即 + = c + )的解是x1=c,x2=-; x+ = c + 的解是x1=c,x2=; x+ = c + 的解是x1=c,x2=;… (1)请观察上述方程与解的特征,比较关于x的方程x+ = c+ (m≠0)与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证. (2)由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:x+ = a + . 参考答案 1.B 2.C 3.C 4.D 5.A 6.C 7.A 8.D 9.b3 10.xy 11.2 12. 13.-2 14.3 15.(1)解: ①- ② (2)解:①最简公分母是36a4b3,- ,,-. ②最简公分母是(x+2)(x-2),,,-. 16.(1)解: x=-1且y≠±1. (2)解:-1 17.(1)解:x=3 (2)解:x= 18. 解:(1)A·B=( - ) × = × =2x+8. (2)答案不唯一.如,“逆向”问题一:已知A·B=2x+8,B=,求A. 解答:A=(A·B)÷B=(2x+8)÷ = . “逆向”问题二:已知A·B=2x+8,A= - .求B. 解答:B=(A·B)÷A=(2x+8)÷( - ) =(2x+8) ÷ =2(x+4)× = . 19. 解:设公共汽车的速度为x千米/小时,则小汽车的速度为3x千米/小时, 由题意可列方程为 -2- = , 解得x=20. 经检验x=20符合题意, 故3x=60. 即公共汽车的速度为20千米/小时,小汽车的速度为60千米/小时. 20.解:(1)x1=c,x2=. (2)∵x+ = a + , ∴x-1 + = a-1+ , 由(1)可得:x-1=a-1或x-1=, ∴x1=a,x2=.查看更多