2020八年级数学上册 第13章 轴对称 最短路径问题

2020八年级数学上册 第13章 轴对称 最短路径问题

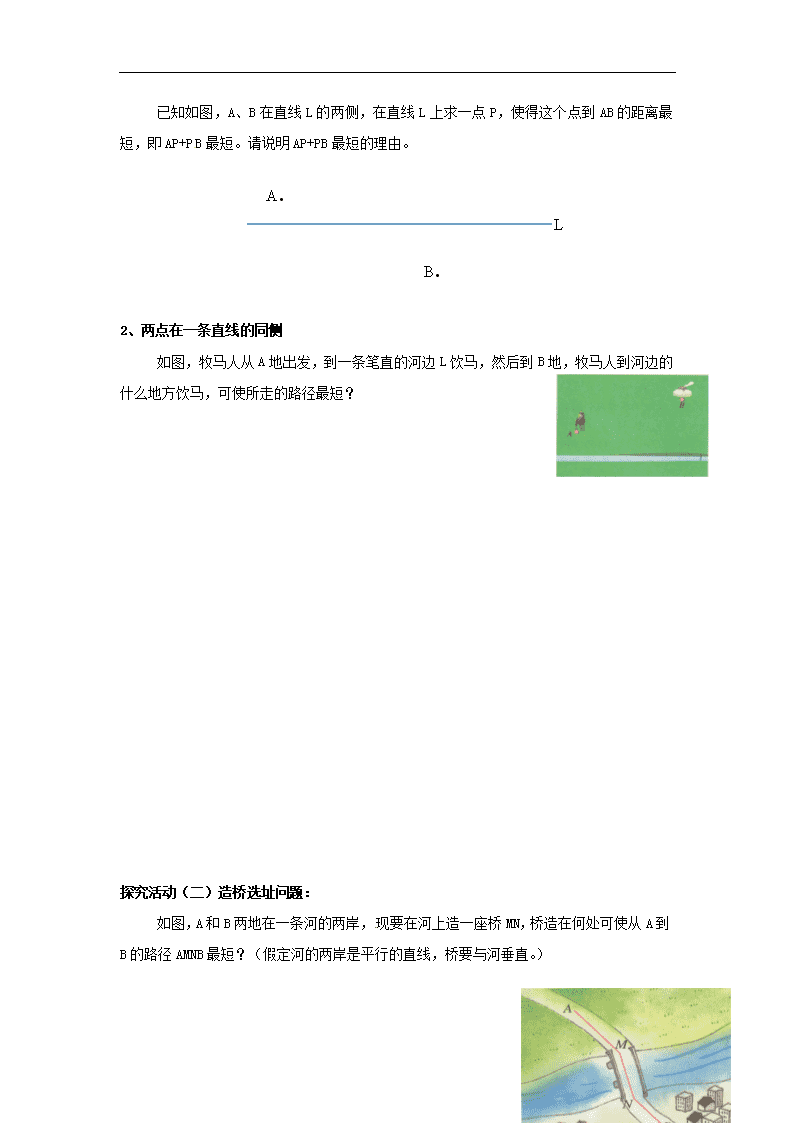
课题：13.4 课题学习：最短路径问题 ‎ ‎【学习目标】‎ ‎1、了解解决最短路径问题的基本策略和基本原理。‎ ‎2、能将实际问题中的“地点”“河”“桥”等抽象为数学中的“点”“线”，使实际问题数学化。‎ ‎3、能运用轴对称、平移变化解决简单的最短路径问题，体会几何变化在解决最值问题中的重要作用。‎ ‎4、在探索最短路径的过程中，感悟、运用转化思想。进一步培养好奇心和探究心理，更进一步体会到数学知识在生活中的应用。‎ ‎【学习重难点】‎ 重点： 利用轴对称将最短路径问题转化为“两点之间，线段最短”问题。‎ 难点： 如何利用轴对称、平移变化将最短路径问题转化为线段和最小问题。‎ 一、知识链接 复习旧知：1.两点之间，_______最短。‎ ‎2.连接直线外一点与直线上各点的所有线段中_______最短。‎ ‎3． 如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的_________。类似的，轴对称图形的对称轴，是任何一对对应点所连线段的_______ 。‎ ‎4．平移性质：(1)平移前后图形的形状和大小________。(2)对应点连线______________。 ‎ 自主学习（新知）： 精读课本第85-87页，用红色的笔对有关概念进行勾画并找出自己的疑惑和要讨论的问题，准备在课堂上讨论质疑。‎ ②‎ A B ①‎ ③‎ 如图所示，从A地到B地有三条路选择，你会选走那条路最近？你的理由是什么？‎ 二、合作与探究 探究活动（一）将军饮马问题：1、两点在一条直线的异侧：‎ 6‎ 已知如图，A、B在直线L的两侧，在直线L上求一点P，使得这个点到AB的距离最短，即AP+PB最短。请说明AP+PB最短的理由。‎ A.‎ B.‎ L ‎2、两点在一条直线的同侧 如图，牧马人从A地出发，到一条笔直的河边L饮马，然后到B地，牧马人到河边的什么地方饮马，可使所走的路径最短？‎ 探究活动（二）造桥选址问题：‎ 如图，A和B两地在一条河的两岸，现要在河上造一座桥MN，桥造在何处可使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直。）‎ 6‎ 三、巩固练习 基础练习： ‎ 如图，MNPQ是一张台球桌子，桌上球A与球B之间有其他球阻隔，现在要打A球，经桌边MN、NP两次反弹再碰到B球，请你画出A球的行走路线。‎ 拓展提升：‎ 6‎ ‎1、牧马人从A地出发，先到草地MN某一处牧马，再到河边L饮马，然后回到B处，请画出最短路径。‎ ‎2、如图，点C为∠AOB内一点．‎ ‎（1）在OA求作点D，OB上求作点E，使△CDE的周长最小，请画出图形；‎ ‎ （2）在（1）的条件下，若∠AOB＝30°，OC＝10，求△CDE周长的最小值和此时∠DCE的度数．‎ 四、 要点归纳：‎ 在解决最短路径问题时，我们常利用 、 等变化把已知问题转化为容易解决的问题，从而作出最短路径的选择。‎ 6‎ ‎【问题1】‎ 作法 图形 原理 ‎1‎ 在直线l上 求一点P，使PA+PB值最小．‎ 连AB，与l交点即为P．‎ 两点之间线段最短．‎ PA+PB最小值为 ．‎ ‎2‎ 在直线l上求一点P，使PA+PB值最小．‎ 作B关于l的对称点B＇连A B＇，与l交点即为P．‎ 两点之间线段最短．‎ PA+PB最小值为 ．‎ ‎3将军饮马 在直线、上分别求点M、N，使△PMN的周长最小．‎ 分别作点P关于两直线的对称点P＇和P＇＇，连P＇P＇＇，与两直线交点即为M，N．‎ 两点之间线段最短．‎ PM+MN+PN的最小值为线段 的长．‎ ‎4造桥选址 直线∥，在、，上分别求点M、N，使MN⊥，且AM+MN+BN的值最小．‎ 将点A向下平移MN的长度单位得A＇，连A＇B，交于点N，过N作NM⊥于M．‎ 两点之间线段最短．‎ AM+MN+BN的最小值为 ．‎ 课后反思： . ‎ 6‎ ‎ . ‎ ‎ ‎ ‎（实际 课时）‎ 6‎