- 2021-11-01 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版八年级数学上册第十三章测试题及答案
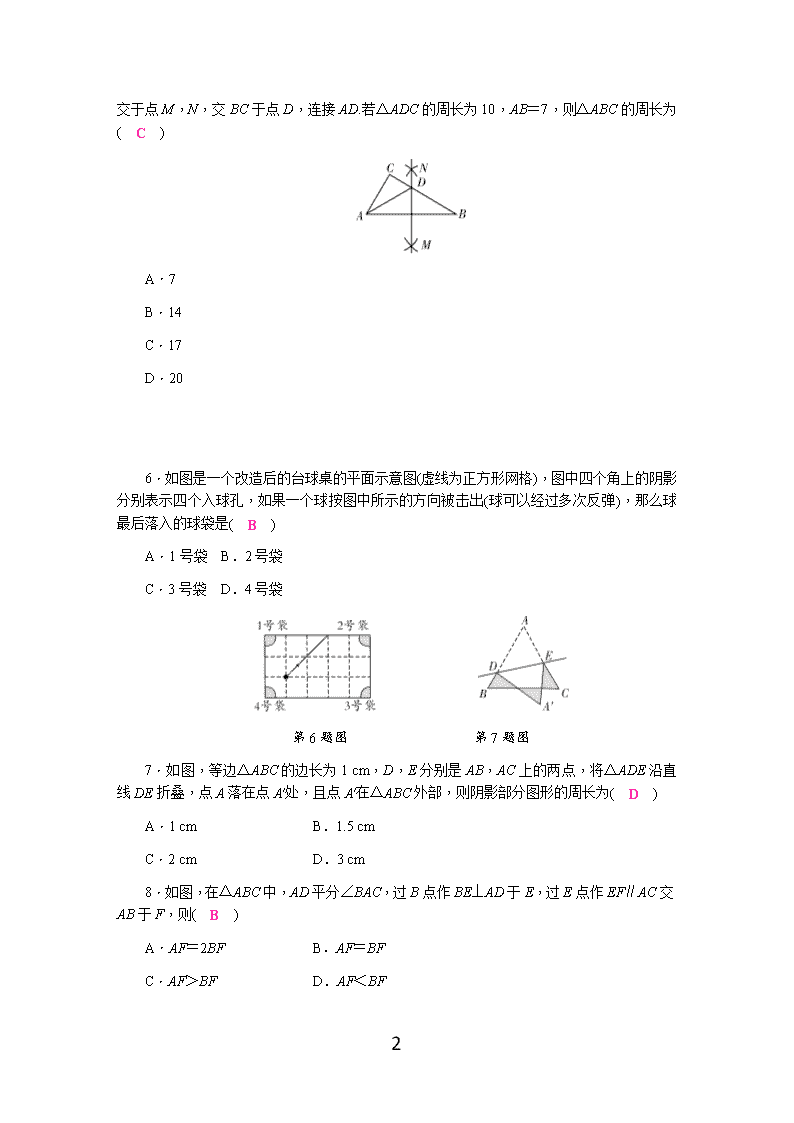
人教版八年级数学上册第十三章测试题及答案 (考试时间:120分钟 满分:120分) 分数:__________ 1 第Ⅰ卷 (选择题 共30分) 一、选择题(每小题3分,共30分) 1.在下列绿色食品、循环回收、节能、节水的四个标志中,属于轴对称图形的是( A ) 2.下列右侧四幅图中,平行移动到位置M后能与N成轴对称的是( C ) A.图① B.图② C.图③ D.图④ 3.下列性质中,等腰三角形具有而直角三角形不一定具有的是( B ) A.两边之和大于第三边 B.有一个角的平分线垂直于这个角的对边 C.有两个锐角的和等于90° D.内角和等于180° 4.下列说法正确的是( C ) A.任何一个图形都有对称轴 B.两个全等三角形一定关于某直线对称 C.若△ABC与△A1B1C1关于某直线成轴对称,则△ABC≌△A1B1C1 D.点A,点B在直线l两旁,且AB与直线l交于点O,若AO=BO,则点A与点B关于直线l对称 5.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧, 10 两弧相交于点M,N,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( C ) A.7 B.14 C.17 D.20 6.如图是一个改造后的台球桌的平面示意图(虚线为正方形网格),图中四个角上的阴影分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么球最后落入的球袋是( B ) A.1号袋 B.2号袋 C.3号袋 D.4号袋 第6题图 第7题图 7.如图,等边△ABC的边长为1 cm,D,E分别是AB,AC上的两点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( D ) A.1 cm B.1.5 cm C.2 cm D.3 cm 8.如图,在△ABC中,AD平分∠BAC,过B点作BE⊥AD于E,过E点作EF∥AC交AB于F,则( B ) A.AF=2BF B.AF=BF C.AF>BF D.AF<BF 10 第8题图 第9题图 9.★如图所示的正方形网格中,网格线的交点称为格点,已知A,B是两格点,如果点C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( C ) A.6个 B.7个 C.8个 D.9个 10.★如图,在△ABC中,AB=AC,∠BAC=90°,∠EPF为直角且∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于E,F,给出以下四个结论:①AE=CF;②△PEF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的有( C ) A.1个 B.2个 C.3个 D.4个 第10题图 第12题图 第Ⅱ卷 (非选择题 共90分) 二、填空题(每小题3分,共24分) 11.已知点P1(a-1,2 020)和P2(2 017,b-1)关于x轴对称,则a+b= -1 . 12.如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=8,CD=5,则△ABC的周长是 26 . 13.如图,在△ABC中,AD⊥BC于D,请你再添加一个条件,就可以确定△ABC是等腰三角形,你添加的条件是 BD=CD(或∠BAD=∠CAD) . 10 第13题图 第14题图 14.如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC相交于点E,若AD=BD,则折痕BE的长为 4 . 15.等腰三角形的顶角和一个底角的度数之比是4∶1,则这个等腰三角形的底角度数为 30° . 16.★如图,AB=AC,AE=EC=CD,∠A=60°,若EF=2,则DF= 6 . 第16题图 第17题图 17.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,在AB上截取AA′=AC,连接A′C,作B′C⊥A′C,且B′C=BC,连接BB′,A′B′,若BC=2,则BB′的长度为 2 . 18.★在Rt△ABC中,∠ACB=90°,∠B=30°,D是AB的中点,E是AD上一点,连接CE,以CE为边向右作等边三角形CEF,∠BCF=10°,连接DF,则∠DFE的度数为 40°或20° . 选择、填空题答题卡 一、选择题(每小题3分,共30分) 题号 1 2 3 4 5 得分 答案 A C B C C 题号 6 7 8 9 10 答案 B D B C C 二、填空题(每小题3分,共24分)得分:______ 11. -1 12. 26 13. BD=CD(或∠BAD=∠CAD) 14. 4 15. 30° 16. 6 10 17. 2 18. 40°或20° 三、解答题(共66分) 19.(8分)如图,在所给网格图(每小格边长均是1的正方形)中完成下列各题: (1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1; (2)在DE上画出点P,使PB1+PC最小. 解:(1)△A1B1C1如图所示. (2)连接B1C交DE于点P,则P点就是所求的点.如图所示. 20.(8分)如图,在△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作: ①作∠BAC的平分线AM交BC于点D; ②作边AB的垂直平分线EF,EF与AM相交于点P; ③连接PB,PC. 请你观察图形解答下列问题: (1)线段PA,PB,PC之间的数量关系; (2)若∠ABC=70°,求∠BPC的度数. 解:(1)PA=PB=PC. (2)∵AB=AC, ∴∠ABC=∠ACB=70°, ∴∠BAC=180°-70°×2=40°. ∵AM平分∠BAC, 10 ∴∠BAD=∠CAD=20°. ∵PA=PB=PC, ∴∠ABP=∠BAP=∠ACP=20°. ∴∠BPC=∠ABP+∠BAC+∠ACP= 20°+40°+20°=80°. 21.(8分)如图,在等边△ABC中,AD⊥BC于D点,BD=2,以AD为一边向右作等边△ADE. (1)求△ABC的周长; (2)判断AC,DE的位置关系,并说明理由. 解:(1)∵AD⊥BC, 在Rt△ABD中, ∠B=60°, ∴∠BAD=30°,BD=2, ∴AB=2BD=4, ∴△ABC的周长为4×3=12. (2)AC⊥DE.理由: ∵在△ADF中, ∠DAC=30°,∠ADF=60°, ∴∠AFD=180°-30°-60°=90°, ∴AC⊥DE. 22.(8分)将一幅直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30° 角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD相交于点O,连接CD.求证:△CDO是等腰三角形. 10 证明:在△BCD中, ∵∠CBD=30°, BC=BD, ∴∠BCD=∠BDC=(180°-30°)=75°, ∠COD=∠CBO+∠BCO=45°+30°=75°, ∴∠BDC=∠COD=75°, ∴CO=CD. ∴△COD是等腰三角形. 23.(10分)如图,在△ABC中,AB=AC,△BEN的边BN在BC上,点E在△ABC的内部,∠E=∠EBC=60°,AD平分∠BAC交EN于点D.若BE=6 cm,DE=2 cm,求BC的长. 解:延长AD交BC于点M, ∵AB=AC,AD平分∠BAC, ∴AM⊥BC, BM=CM=BC, ∵∠E=∠EBN=60°, ∴△BEN为等边三角形, ∴EN=BN=BE=6 cm,DN=6-2=4 (cm). 在Rt△DMN中,∠BND=60°,∠MDN=30°, 10 ∴MN=DN=2 cm,∴BM=6-2=4 cm, ∴BC=2BM=8 cm. 24.(12分)如图,在△ABC中,∠ABC=45°,点P是边BC上的一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为D,连接BD,△APC的PC边上的高为AH. (1)求∠BPD的大小; (2)判断直线BD,AH是否平行?并说明理由; (3)求证:∠BAP=∠CAH. (1)解:∵∠PAB=15°,∠ABC=45°, ∴∠APC=60°. ∵点C关于直线PA的对称点为D, ∴PD=PC,AD=AC, ∴△ADP≌△ACP(SSS), ∴∠APC=∠APD=60°,∴∠BPD=60°. (2)解:直线BD,AH平行.理由: ∵BC=3BP,∴BP=PC=PD. 取PD中点E,连接BE, 则△BEP为等边三角形, △BDE为等腰三角形,∴∠BEP=60°, ∴∠BDE=∠BEP=30°,∴∠DBP=90°. ∵△APC的PC边上的高为AH, ∴AH⊥BC,∴BD∥AH. (3)证明:过点A作BD,DP的垂线,垂足分别为G,F. 10 ∵∠APC=∠APD,∴AH=AF. ∵∠CBD=90°,∠ABC=45°, ∴∠GBA=∠CBA,∴AG=AH, ∴AG=AF,∴点A在∠GDP的平分线上. ∵∠BDP=30°,∴∠GDP=150°, ∴∠ADP=75°,∴∠C=∠ADP=75°. ∴Rt△ACH中,∠CAH=15°, ∴∠BAP=∠CAH. 25.(12分)如图①所示,点P,Q分别是等边△ABC的边AB,BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的运动速度相同,连接AQ,CP交于点M. (1)求证:△ABQ≌△CAP; (2)当点P,Q分别在AB,BC边上运动时,∠QMC的度数会发生变化吗?若变化,请说明理由;若不变,求出它的度数; (3)如图②所示,若点P,Q运动到终点后继续在AB,BC的延长线上运动,直线AQ,CP的交点为M,则∠QMC的度数会发生变化吗?若变化,请说明理由;若不变,求出它的度数. (1)证明:∵△ABC是等边三角形, ∴∠ABQ=∠CAP=60°,AB=AC. ∵点P,Q运动速度相同,∴AP=BQ. 在△ABQ和△CAP中, ∴△ABQ≌△CAP(SAS). (2)解:点P,Q在AB,BC边上运动的过程中,∠QMC的度数不变. 理由如下: 由(1)得,△ABQ≌△CAP,∴∠BAQ=∠ACP, 10 ∵∠QMC是△ACM的外角, ∴∠QMC=∠ACP+∠MAC =∠BAQ+∠MAC =∠BAC. ∵∠BAC=60°,∴∠QMC=60°. (3)解:点P,Q运动到终点后继续在射线AB,BC上运动时,∠QMC不变. 理由如下: 易证△ABQ≌△CAP, ∴∠BAQ=∠ACP,即∠PAM=∠ACP. ∴∠QMC=∠PAM+∠APM =∠ACP+∠APM =180°-∠PAC=180°-60°=120°. 故若点P,Q运动到终点后继续在射线AB,BC上运动时,∠QMC度数不变. 10查看更多