- 2021-11-01 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版八年级数学(下册)第一章测试卷(附答案)
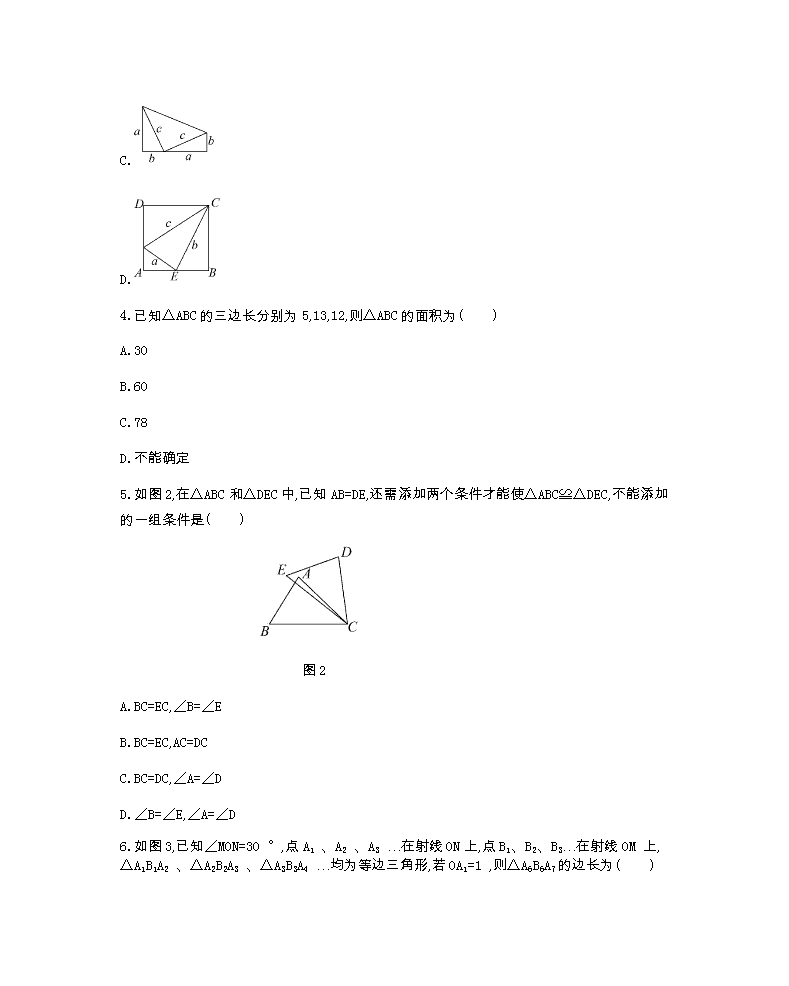
北师八下数学测试卷第一章 1.下列说法错误的是( ) A.斜边和一锐角对应相等的两个直角三角形全等 B.有两边对应角相等的两个直角三角形全等 C.有两个锐角相等的两个直角三角形全等 D.有一直角边和一锐角对应相等的两个直角三角形全等 2.如图1,∠C=90°,DE垂直平分AB,DC=DE,则∠ADC的度数为( ) 图1 A.40° B.50° C.60° D.70° 3.下列选项中,不能用来证明勾股定理的是( ) A. B. C. D. 4.已知△ABC的三边长分别为5,13,12,则△ABC的面积为( ) A.30 B.60 C.78 D.不能确定 5.如图2,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( ) 图2 A.BC=EC,∠B=∠E B.BC=EC,AC=DC C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D 6.如图3,已知∠MON=30 °,点A1 、A2 、A3 …在射线ON上,点B1、B2、B3…在射线OM 上,△A1B1A2 、△A2B2A3 、△A3B3A4 …均为等边三角形,若OA1=1 ,则△A6B6A7的边长为( ) 图3 A.6 B.12 C.32 D.64 7.已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法: ①如果添加条件“AB=AC”,那么△ABC是等边三角形; ②如果添加条件“∠B=∠C”,那么△ABC是等边三角形; ③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形. 上述说法中,正确的说法有( ) A.3个 B.2个 C.1个 D.0个 8.如图4,在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F,使DF=DE,连接FC,若∠B=70°,则∠F的度数是( ) 图4 A.40° B.70° C.50° D.45° 9.已知一个三角形的边长分别是6 cm,8 cm,10 cm,则它的面积是 cm2. 10.若A、B、C为三个正整数,且A+B+C=12,则以A、B、C为边所组成的三角形可以是:①等腰三角形;②等边三角形;③直角三角形,你认为以上符合条件的正确结论的序号是 . 11.如图5,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为 . 图5 12.如图6,∠AOB=30°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD等于 . 图6 13.如图7,MN∥PQ,AB⊥PQ,点A、D和点B、C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB= . 图7 14.如图8,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为 个. 图8 15.如图9,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF. 求证:(1)PE=PF; (2)点P在∠BAC的角平分线上. 图9 16.如图10,在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F.求证:AD垂直平分EF. 图10 17.已知:如图11,在Rt△ABC中,∠A=90°,CD平分∠ACB交边AB于点D,DE⊥BC,垂足为E,AD=BD.求证:BE=CE. 图11 18.如图12,在△ABC中,AB=AC,点D是BC的中点,点E在AD上. (1)求证:BE=CE; (2)如图13,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变.求证:△AEF≌△BCF. 图12 图13 19.如图14,△ABC为正三角形,D为边BA延长线上一点,连接CD,以CD为一边作正三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由. 图14 20.(1)如图15是一个重要公式的几何解释,请你写出这个公式; (2)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图16证明了勾股定理(1876年4月1日发表在《新英格兰教育日志》上),现请你尝试写出证明过程,说明:c2=a2+b2. 图15 图16 参考答案 1.C 2.C 3.D 4.A 5.C 6.C 7.A 8.A 9.24 10.①②③ 11.13 12.3 13.7 14.6 15.证明:(1)如图,连接AP并延长. ∵PE⊥AB,PF⊥AC, ∴∠AEP=∠AFP=90°. 又AE=AF,AP=AP, ∵在Rt△AFP和Rt△AEP中, ∴Rt△AEP≌Rt△AFP(HL). ∴PE=PF. (2)∵Rt△AEP≌Rt△AFP, ∴∠EAP=∠FAP. ∴AP是∠BAC的角平分线. 故点P在∠BAC的角平分线上. 16.证明:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC, ∴DE=DF,∠AED=∠AFD=90°. 在Rt△AED和Rt△AFD中, ∴Rt△AED≌Rt△AFD(HL), ∴AE=AF. ∵AD是∠BAC的平分线, ∴AD垂直平分EF(三线合一). 17.证明:∵∠A=90°,DE⊥BC,CD平分∠ACB, ∴AD=DE. ∵AD=BD, ∴DE=BD. 在Rt△BDE中,∵DE=BD, ∴∠B=30°. 在Rt△ABC中, ∵∠A=90°,∠B=30°, ∴∠ACB=60°. ∵CD平分∠ACB, ∴∠BCD=∠ACB=30°. ∴∠BCD=∠B, ∴BD=CD. ∵DE⊥BC, ∴BE=CE. 18.证明:(1)∵AB=AC,D是BC的中点, ∴∠BAE=∠EAC. 在△ABE和△ACE中, ∴△ABE≌△ACE(SAS). ∴BE=CE. (2)∵∠BAC=45°,BF⊥AF, ∴△ABF为等腰直角三角形. ∴AF=BF. ∵AB=AC,点D是BC的中点, ∴AD⊥BC. ∴∠EAF+∠C=90°. ∵BF⊥AC, ∴∠CBF+∠C=90°. ∴∠EAF=∠CBF. 在△AEF和△BCF中, ∴△AEF≌△BCF(ASA). 19.解:AE∥BC.理由如下: ∵△ABC与△CDE为正三角形, ∴BC=AC,CD=CE,∠ACB=∠DCE=60°. ∴∠ACB+∠ACD=∠DCE+∠ACD, 即∠BCD=∠ACE. ∴△BCD≌△ACE. ∴∠B=∠EAC. ∵∠B=∠ACB, ∴∠EAC=∠ACB. ∴AE∥BC. 20.解:(1)(a+b)2=a2+2ab+b2; (2)∵Rt△DEC≌Rt△EAB, ∴∠DEC=∠EAB. ∵∠EAB+∠AEB=90°, ∴∠DEC+∠AEB=90°. ∴△AED为等腰直角三角形. ∵S梯形ABCD=SRt△ABE+SRt△DCE+SRt△DEA, ∴(b+a)(a+b)=ab + ab + c2,即(a+b)2=2ab+c2, ∵(a+b)2=a2+2ab+b2, ∴a2+2ab+b2=2ab+c2, ∴c2=a2+b2.查看更多