八年级上数学课件八年级上册数学课件《全等三角形的判定》 人教新课标 (2)_人教新课标

八年级上数学课件八年级上册数学课件《全等三角形的判定》 人教新课标 (2)_人教新课标

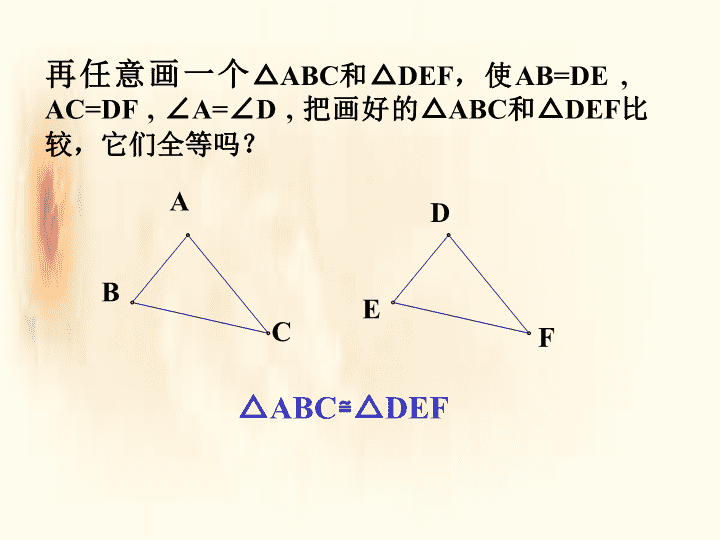
全等三角形的判定 （SAS） 画△ABC,使AB=3cm，AC=4cm。 画法： 2. 在射线AM上截取AB= 3cm 3. 在射线AN上截取AC=4cm 这样画出来的三角形与同桌所画的三角形进行比 较，它们互相重合吗？ 若再加一个条件，使∠A=45°，画出△ABC 1. 画∠MAN= 45° 4.连接BC 则△ABC就是所求的三角形 把你们所画的三角形剪下来与同桌所画的三角形进行 比较，它们能互相重合吗？ 再任意画一个△ABC和△DEF，使AB=DE , AC=DF , ∠A=∠D , 把画好的△ABC和△DEF比 较，它们全等吗？ A B C D E F △ABC≌ △DEF 由前边的作图比较过程，我们可以得出什么结论？ 用符号语言表达为： 在△ABC与 △DEF中 AB=DE ∠A=∠D AC=DF ∴△ABC≌ △DEF（SAS） A B C D E F    例2、如图，有一池塘，要测池塘两端A、B 的距离，可先在平地上取一个可以直接到达 A和B的点C，连接AC并延长到D，使CD=CA.连 接BC并延长到E，使CE=CB.连接DE，那么量 出DE的长就是A、B的距离.为什么？ 分析：如果能证明 △ABC≌ △DEC ，就可 以得出AB=DE. 在△ABC和△DEC中， CA=CD , CB=CE .如果能得出 ∠ACB=∠DCE， △ABC和 △DEC就全等了 A B C DE 证明： 在△ABC和△DEC中 CA=CD ∠ACB=∠DCE CB=CE    ∴△ABC≌ △DEC（SAS） ∴AB=DE 已知：如图， AB=CB ，∠ ABD= ∠ CBD 。 问AD=CD， BD 平分∠ ADC 吗？ A B C D 证明：在△ABD与△CBD中    AB=CB ∠ABD=∠CBD BD=BD ∴△ABD≌ △CBD（SAS） ∴AD=CD ∠ADB=∠CDB 即BD平分∠ADC 因为全等三角形的对应角相等， 对应边相等，所以，证明分别属于两 个三角形的线段相等或角相等的问题， 常常通过证明两个三角形全等来解决。 由前边两个题目可以看出： 探究 n 两边和它们的夹角对应相等的两个三角 形全等。由“两边及其中一边的对角对 应相等”的条件能判定两个三角形全等 吗？为什么？ 动画演示 这说明：有两边和其中一 边的对角对应相等的两个 三角形不一定全等。 例: 已知有4个三角形，它们有如下的关 系： A1B1＝A2B2＝A3B3＝AB， ∠B1＝∠B2＝∠B3＝∠B， B1C1＜B2C2＝BC＜B3C3 ． 问△ABC与其余三个三角形中的哪一个 全等． 【解】我们把甲、乙、丙三个三角形移动后覆盖在△ABC 上，使得A1B1，A2B2，A3B3和AB重合，∠B1、∠B2、 ∠B3和∠B重合，C1和C2、C3将落在直线BC上，其中： (1)由于B1C1＜BC，所以点C1在C的左侧，可知△A1B1C1 和△ABC不全等； (2)由于B3C3＞BC，所以点C3在点C的右侧， 可知△A3B3C3和△ABC也不全等； (3)由于B2C2＝BC，所以点C2和点C重合，于是B2C2与 BC重合，A2C2和CA也重合，则可知△A2B2C2与△ABC 重合，即 △A2B2C2≌ △ABC ． 1、如图，B点在A点的正北方向。两车从路段AB的一 端A出发，分别向东、向西进行相同的距离，到达C、 D两地。此时C，D到B的距离相等吗？为什么？ B D A C 【证明】∵在△BAD和△BAC中， BA=BA ∠BAD=∠BAC AD=AC 则△BAD≌ △BAC (SAS). 即BD=BC 2、如图，点E、F在BC上，BE=CF， AB=DC， ∠B=∠C，求证： ∠A=∠D A D B E F C 【证明】∵BF=BE+EF CE=CF+FE 而BE=CF ∴BF=CE 在△ABF和△DCE中， BF=CE ∠B=∠C AB=DC 则△BAD≌ △BAC (SAS). 即∠A=∠D 已知:如图，AD∥BC，AD＝CB. 　　　　　　 求证:AB＝CD. 【提示】连结AC， 由 △ABC≌ △CDA 故 AB＝CD. A D B C 课堂小结: 2. 用尺规作图：已知两边及其夹角的三角形 1. 三角形全等的条件,两边和它们的夹角对应相等 的两个三角形全等 (边角边或SAS) 课本104页3、4题 同步练习 布置作业：