八年级下册数学同步练习4-2 一次函数 湘教版

八年级下册数学同步练习4-2 一次函数 湘教版

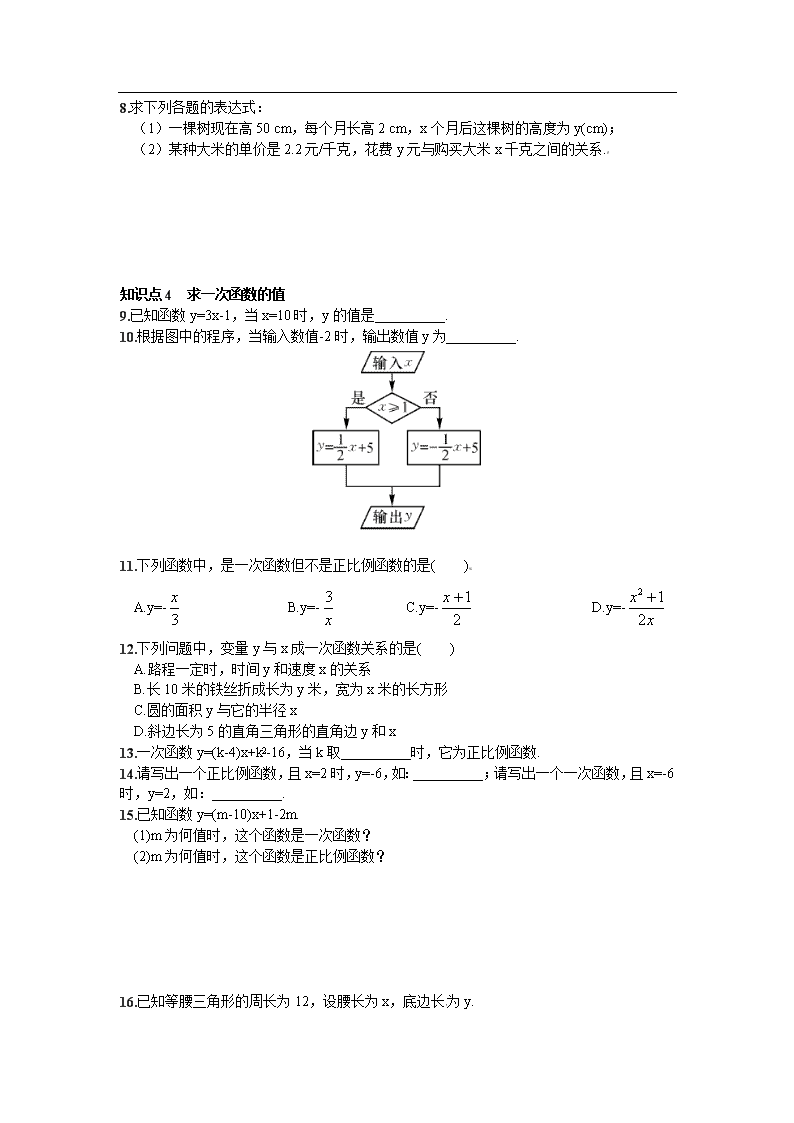
‎4.2 一次函数 要点感知1 如果函数的解析式是自变量的__________，那么这样的函数称为一次函数，它的一般形式是__________.特别地，当b=0时，一次函数y=kx(k为常数，k≠0)也叫作正比例函数，其中k叫作比例系数.‎ 预习练习1-1 下列函数：①y=x；②y=；③y=；④y=2x+1，其中一次函数的个数是( )‎ ‎ A.1 B.2 C.3 D.4‎ ‎1-2下列函数中，是正比例函数的是( )‎ ‎ A.y=-8x B.y=-8x+1 C.y=8x2+1 D.y=-‎ 要点感知2 一次函数的特征是：因变量随自变量的变化是__________.‎ 预习练习2-1 在一次函数y=2x-1中，自变量x每增加1，函数值y相应地增加__________.[来源:学,科,网Z,X,X,K]‎ 要点感知3 一次函数y=kx+b(k，b为常数，k≠0)的自变量取值范围是__________，但在实际问题中，要根据具体情况来确定它的自变量的取值范围.‎ 预习练习3-1 火车以40千米/时的速度行驶，它走过的路程s(千米)与时间t(小时)之间的关系式是__________，其中自变量t的取值范围是__________.‎ 知识点1 一次函数的概念 ‎1.下列关于x的函数中，是一次函数的是( )‎ ‎ A.y=3(x-1)2+1 B.y=x+ ‎ ‎ C.y=-x D.y=(x+3)2-x2‎ ‎2.已知函数y=(k+2)x+k2-4，当k__________时，它是一次函数.[来源:学科网]‎ ‎3.已知一次函数y=(k-1)x|k|+3，则k=__________.‎ 知识点2 正比例函数的概念 ‎4.若y=x+2-b是正比例函数，则b的值是( )‎ ‎ A.0 B.-2 C.2 D.-0.5‎ ‎5.若函数y=(a+2)为正比例函数，则a的值为( )‎ ‎ A.-2 B.2 C.0 D.-2或0‎ 知识点3 确定一次函数的表达式 ‎6.如果每盒圆珠笔有12枝，售价18元，那么圆珠笔的销售额y(元)与圆珠笔的销售枝数x之间的函数关系式是( )‎ ‎ A.y=x B.y=x C.y=12x D.y=x ‎7.目前，全球淡水资源日益减少，提倡全社会节约用水.据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升.小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x分钟后，水龙头滴出y毫升的水，请写出y与x之间的函数关系式是( )‎ ‎ A.y=0.05x B.y=5x C.y=100x D.y=0.05x+100‎ ‎[来源:学§科§网]‎ ‎8.求下列各题的表达式：‎ ‎ （1）一棵树现在高50 cm，每个月长高2 cm，x个月后这棵树的高度为y(cm)；‎ ‎ （2）某种大米的单价是2.2元/千克，花费y元与购买大米x千克之间的关系.‎ ‎[来源:学科网ZXXK]‎ 知识点4 求一次函数的值 ‎9.已知函数y=3x-1，当x=10时，y的值是__________.‎ ‎10.根据图中的程序，当输入数值-2时，输出数值y为__________.‎ ‎11.下列函数中，是一次函数但不是正比例函数的是( )‎ ‎ A.y=- B.y=- C.y=- D.y=-‎ ‎12.下列问题中，变量y与x成一次函数关系的是( )‎ ‎ A.路程一定时，时间y和速度x的关系 ‎ B.长10米的铁丝折成长为y米，宽为x米的长方形 ‎ C.圆的面积y与它的半径x ‎ D.斜边长为5的直角三角形的直角边y和x ‎13.一次函数y=(k-4)x+k2-16，当k取__________时，它为正比例函数.‎ ‎14.请写出一个正比例函数，且x=2时，y=-6，如：__________；请写出一个一次函数，且x=-6时，y=2，如：__________.‎ ‎15.已知函数y=(m-10)x+1-2m.‎ ‎ (1)m为何值时，这个函数是一次函数？‎ ‎ (2)m为何值时，这个函数是正比例函数？‎ ‎16.已知等腰三角形的周长为12，设腰长为x，底边长为y.[来源:Z.xx.k.Com]‎ ‎ (1)试写出y关于x的函数解析式，并直接写出自变量x的取值范围；‎ ‎ (2)当x=5时，求出函数值.‎ ‎17.如图，已知正方形ABCD的边长为6，P为BC上一动点，设BP=x，试求四边形APCD的面积y与x的函数表达式(0≤x≤6),并说明它是一次函数还是正比例函数？‎ ‎18.生态公园计划在园内的坡地上造一片有A，B两种树的混合林，需要购买这两种树苗2 000棵，种植A,B两种树苗的相关信息如下表：‎ ‎ 设购买A种树苗x棵，造这片林的总费用为y元，解答下列问题：‎ ‎ (1)写出y(元)与x(棵)之间的函数表达式；‎ ‎ (2)假设这批树苗种植后成活1 960棵，则造这片林的总费用需多少元？‎ 参考答案 要点感知1 一次式 y=kx+b(k，b为常数，k≠0)‎ 预习练习1-1 C ‎1-2 A 要点感知2 均匀的 预习练习2-1 2‎ 要点感知3 实数集 预习练习3-1 s=40t t≥0‎ ‎1.D 2.≠-2 3.-1 4.C 5.B 6.A 7.B ‎8.（1）y=2x+50;‎ ‎ （2）y=2.2x.‎ ‎9.29 10.6‎ ‎11.C 12.B 13.-4 14.y=-3x(答案不唯一) y=x+8(答案不唯一)‎ ‎15.(1)根据一次函数的定义可得m-10≠0，∴m≠10,这个函数是一次函数；‎ ‎ (2)根据正比例函数的定义，可得m-10≠0且1-2m=0.解得m=.即m=时，这个函数是正比例函数.‎ ‎16.(1)由题意得12=2x+y，‎ ‎∴可得y=12-2x.‎ 根据三角形两边之和大于第三边，两边之差小于第三边可得：y＜2x，2x＜12.‎ ‎∴可得3＜x＜6.‎ ‎ (2)由(1)，得y=12-2x.‎ ‎∴当x=5时，函数值y=2.‎ ‎17.y=6×6-×6x=36-3x(0≤x≤6).它是一次函数，但不是正比例函数.‎ ‎18.(1)y=(15+3)x+(20+4)(2 000-x),即y=-6x+48 000.‎ ‎ (2)由题意，得0.95x+0.99(2 000-x)=1 960.解得x=500.‎ 当x=500时，y=-6×500+48 000=45 000.‎ 答：造这片林的总费用需45 000元.‎