八年级上数学课件《一次函数的图像》 (13)_苏科版

八年级上数学课件《一次函数的图像》 (13)_苏科版

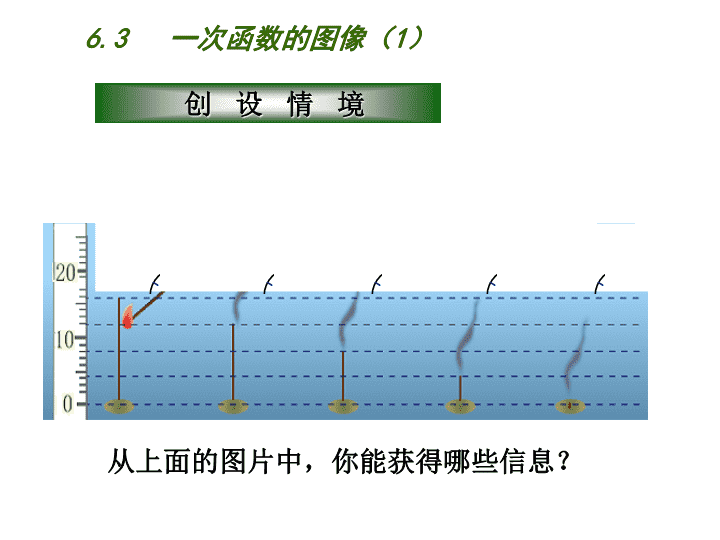
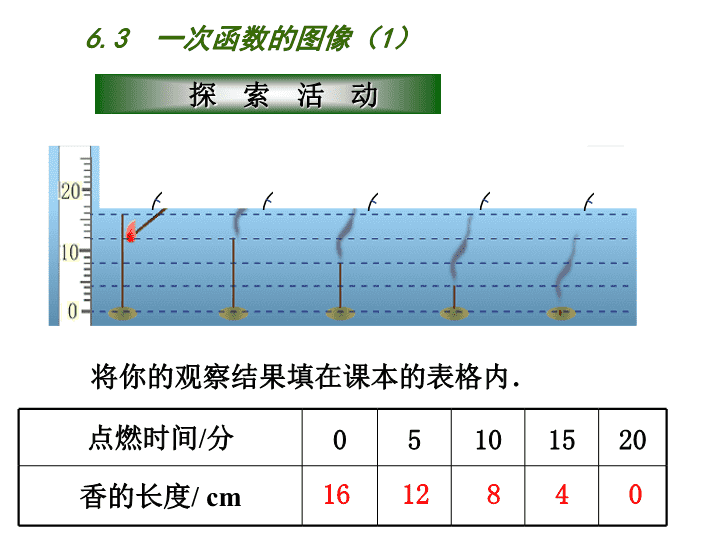
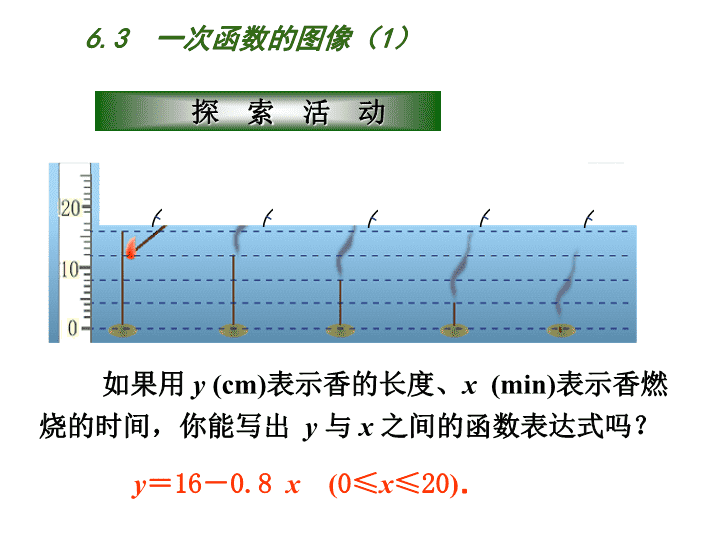
从上面的图片中，你能获得哪些信息？ 6.3　 一次函数的图像（1） 点燃时间/分 0 5 10 15 20 香的长度/ cm 16 12 8 4 0 将你的观察结果填在课本的表格内． 6.3　一次函数的图像（1） 　　 如果用 y (cm)表示香的长度、x (min)表示香燃 烧的时间，你能写出 y 与 x 之间的函数表达式吗？ y＝16－0.8 x (0≤x≤20)． 6.3　一次函数的图像（1） 　　依次连接图片中香的顶端 ，你有什么发现？ 香的顶端在一条直线上． 6.3　一次函数的图像（1） 　　在这个坐标系中，点的横坐标表示香燃烧的时间， 纵坐标表示香的长度． x y O 你能用平面直角坐标系，将图片所揭示的信息及 你的发现告诉大家吗？ 5 10 15 20 20 10 6.3　一次函数的图像（1） x (0，16) (5，12) (10，8) (15，4) (20，0) y 　　这5个点在同一条 直线上吗？ 　　这些点都在一条 直线上. 6.3　一次函数的图像（1） 以x轴表示点燃时间，以y轴表示香的长度，建立直 角坐标系，并分别描点(0，16)、 (5，12)、(10，8)、 (15，4)、(20，0)． x (0，16) (5，12) (10，8) (15，4) y 这 5 个点的坐标都满足y＝16－0.8x吗？ y＝16－0.8 x 这 5 个点的坐标都满足y＝16－0.8x！ 6.3　一次函数的图像（1） x (0，16) (5，12) (10，8) (15，4) y y＝16－0.8x 　　一次函数的图像是什么？ 怎样画一次函数的图像？ 6.3　一次函数的图像（1） 　　通常，我们按下面的步骤，在直角坐标系 中画一次函数y＝2x＋1的图像． （1）列表； （2）描点； （3）连线． 6.3　一次函数的图像（1） （1）列表． 表中x的值如何选取？表中y的值如何确定？ x … 　 　 　 　 … y＝2x＋1 … 　 　 　 　 　 … －2 －1 0 1 2 这样我们就得到了函数图像上的5个点的坐标： (－2，－3)、(－1，－1)、(0，1)、(1，3)、(2，5)． 5－3 －1 1 3 6.3　一次函数的图像（1） • • • • • -3 -2 -1 o 1 2 3 -1 -2 -3 1 2 3 x y y＝2x＋1 （2） 描点： (－2，－3)、(－1，－1)、(0，1) (1，3)、(2，5)． （3）连线. 为什么要“连线”？怎样连线？ 4 6.3　一次函数的图像（1） 仿照刚才方法画一次函数 y＝－x＋2的图像． 思考：画一次函数图像的一般步骤是什么？ 一次函数的图像是什么样的图形？ 6.3　一次函数的图像（1） （1）列表；（2）描点；（3）连线． 结论: 画一次函数图像的一般步骤: 一次函数y＝kx＋b（k，b都为常数且k≠0）可以 用直角坐标系中的一条直线来表示，这条直线也叫做 一次函数y＝kx＋b的图像，以后就称它为： 直线 y＝kx＋b ． 6.3　一次函数的图像（1） 画一次函数的图像有没有简捷的方法呢？ 画一次函数y＝－x＋2的图像时，只要确定 两个点的位置，这是因为： ． 议一议：通常选取哪两点比较方便？ 两点确定一条直线 6.3　一次函数的图像（1） 例：在直角坐标系中，画一次函数y＝－3x＋3的图像． 解：把 x＝0 代入y＝－3x＋3 得 y＝3． 把 y＝0 代入y＝－3x＋3 得 x＝1． 　　过点(0，3)、(1，0)画一条直线， 这条直线就是函数y＝－3x＋3的图像． y -3 -4 4 3 -2 -1 2 1 o 3-2 -1 21 x3--2 --1 21 y -3 -4 -2 -1 2 1 y -3 - -2 -1 2 1 o x 试判断：在点A（2，5）、B（－1，6）、 C（3，12）、 D（－2，3）、E（5，-12）中，哪些点在此函数的图像上？ 6.3　一次函数的图像（1） y＝－3x＋3 仿照刚才方法画一次函数 y＝2x的图像． 6.3　一次函数的图像（1） x 　 　 y=2x 　 　 y=2x x y 0 1 1 2 2 ⑴列表 ⑵描点 ⑶连线 0 0 2 1 小结：正比例函数y＝kx(k≠0)的图象是一条经过原点 的直线. 画图象时一般取点（0，0）、（1，k). 6.3　一次函数的图像（1） 1．下列两点在函数y＝－2x＋3图像上的是 ( ) A．原点和点(1，1)； B．点(1，1)和点(2，3)； C．点(0，3)和点(1，1)； D．点(0，3)和点(2，3)．． C 　　说明：判断一个点是否在函数的图像上，既可 以利用描点直接判断，也可以通过计算加以说明． 6.3　一次函数的图像（1） 1 42 3-4 -1-3 -2 1 4 2 3 -4 -1 -3 -2 0 y x x 0 y＝2x＋2 0 x 0 y＝2x－1 0 x 0 y＝2x－2 0 2. 在同一坐标系中，画一次函数y＝2x＋2、y＝2x－1、　 y＝2x－2的图像. 观察这3个函数的图像，你有什么发现？ y＝2x＋2 y＝2x－1 y＝2x－2 6.3　一次函数的图像（1） 　　3．画出函数y＝－3x＋2的图像，并指出图像所经 过的象限； 　　③求此直线与坐标轴所围成的三角形面积. 　　②求出此直线与坐标轴交点的坐标； 　　①试判断点P（2，5）是否在此函数的图像上，并 说明理由． 6.3　一次函数的图像（1） 1．一次函数图像的形状是一条 ，因此画 一次函数的图像只需要确定图像上的 个 点，就能画出一次函数的图像． 2．一次函数y＝4x－3的图像与x轴的交点坐标 是 　 　　；与y轴的交点坐标是 ． 3．已知点p（2，－1）在一次函数y ＝ mx＋3 的图像上，则m的值是 ． 直线 两 （0，－3） －2 （ ，0） 3 4 6.3　一次函数的图像（1） 6.3　一次函数的图像（1） 1．作一次函数图像的步骤是 ． 2．知道一次函数y＝kx＋b(k≠0)的图像是 　　； 因此在作图时，只要确定两点就可以了． 一般找直线与坐标轴（x、y轴）的2个交点． 一条直线 （1）列表；（2）描点；（3）连线 6.3　一次函数的图像（1） 　 已知一次函数y＝x＋2与y＝－2x＋3 ， 　（1）在同一直角坐标系中画出上述函数的图像， 并求出它们与坐标轴交点的坐标 ． 　（2）求这两条直线的交点坐标 ． 　（3）求这两条直线与坐标轴所围成的图形面积． 6.3　一次函数的图像（1）