八年级上数学课件八年级上册数学课件《实数》 北师大版 (8)_北师大版

八年级上数学课件八年级上册数学课件《实数》 北师大版 (8)_北师大版

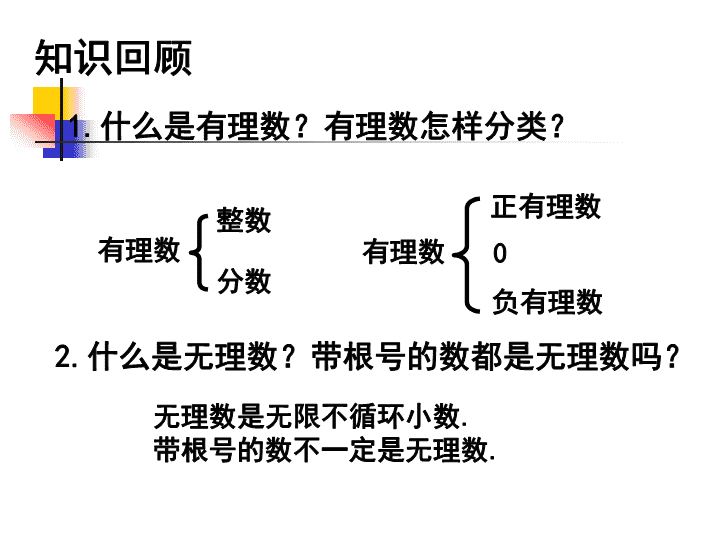
知识回顾 1.什么是有理数？有理数怎样分类？ 整数 分数 有理数 正有理数 负有理数 有理数 0 2.什么是无理数？带根号的数都是无理数吗？ 无理数是无限不循环小数. 带根号的数不一定是无理数. 把下列各数分别填入相应的集合内： , 4 1 ,23 ,7 , , 2 5  ,2 , 3 20 ,5 ,83 , 9 4 ,0 3737737773.0 有理数集合 无理数集合 ,83, 4 1 , 2 5  , 9 4 ,0  ,23 ,7 , ,2 , 3 20 ,5 3737737773.0  学习目标 l 1、了解实数的概念和意义，能按要求对实数 进行分类。 l 2、了解有理数的运算规律在实数范围内仍然 使用。 定 义： 和 统称为实数。 即实数可以分为有理数和无理数 有理数 无理数 实数 无理数有理数 2的相反数为 实数的相关概念 在实数范围内 ，相反数、倒数、绝对值 的意义 ，和有理数范围内的相反数、倒数、 绝对值的意义完全一样。 2 ，绝对值为 ，倒数为2 2 1           )0( )0(0 )0( aa a aa a a 1 a 1. 想一想 3 3  ||  3 5 |3| |0|， 3 5 1 3 0  64 -8 8 8 1 1.在有理数范围内，能进行哪些运算？ 用哪些运算律？   3333 2112742724  2552         5 153 5 153 2.判断下列各式成立吗？ 有理数的运算及运算律对实数仍然适用 想一想 无理数和有理数一样，也有正负之分。 如： 3 是 的，  是 的。正 负 1.你能把下列各数分别填入相应的集合内吗? 正实数集合 负实数集合   ,23 , 4 1 ,7 , ,2 , 3 20 , 9 4 3737737773.0 , 2 5  ,5 ,83 , 4 1 ,23 ,7 , , 2 5  ,2 , 3 20 ,5 ,83 , 9 4 ,0 3737737773.0 二、合作探究（小组合作完成导学案合作探究的第1小题） 按定义分类 按大小分类 议一议 2. 实数可以怎样分类? 实数 有理数 无理数 实数 正实数 负实数 0 议一议 （1） 如图,OA=OB数轴上的点A对 应的数是什么？ 它介于哪 两个整数之间？ （2） 如果将所有有理数都标到数轴上，那么数轴 被填满了吗？ A （3）你能在数轴上找到 对应的点吗？与同伴交流。5 实数与数轴上的点的对应关系： 每一个实数都可以用数轴上的一个点来表示； 反过来，数轴上的每一点都表示一个实数。即实 数和数轴上的点是一一对应的。右边的点表示的 数比左边的点表示的数大。 Ａ 三、练习 1、与数轴上的点一一对应的数是 . 2、在实数 中，分数的个数有 个. 3、 的绝对值，相反数、倒数分别是 . 4、在 （相邻两个2之间的1逐渐增 加），有理数有 ，正整数有 ， 分数有 . 5、化简： = . 6 , 2 2, 3 1  3 27 ...212112111.0,0,8,4, 2 2, 4 1, 3 3   2)23(2321  实数 1 3 1,3,3  0,8,4, 4 1 3 4 4 1 1 四、课堂练习 1．判断下列说法是否正确： （1）无限小数都是无理数； （2）无理数都是无限小数； （3）带根号的数都是无理数。 2．求下列各数的相反数、倒数和绝对值： 49)3(8)2(7)1( 3  ３．在数轴上作出　　对应的点．10 ； ； . 课堂小结 通过今天的学习,说说你的收获和体会? 课外作业: 课本习题2.8