变化的鱼学案（一）

变化的鱼学案（一）

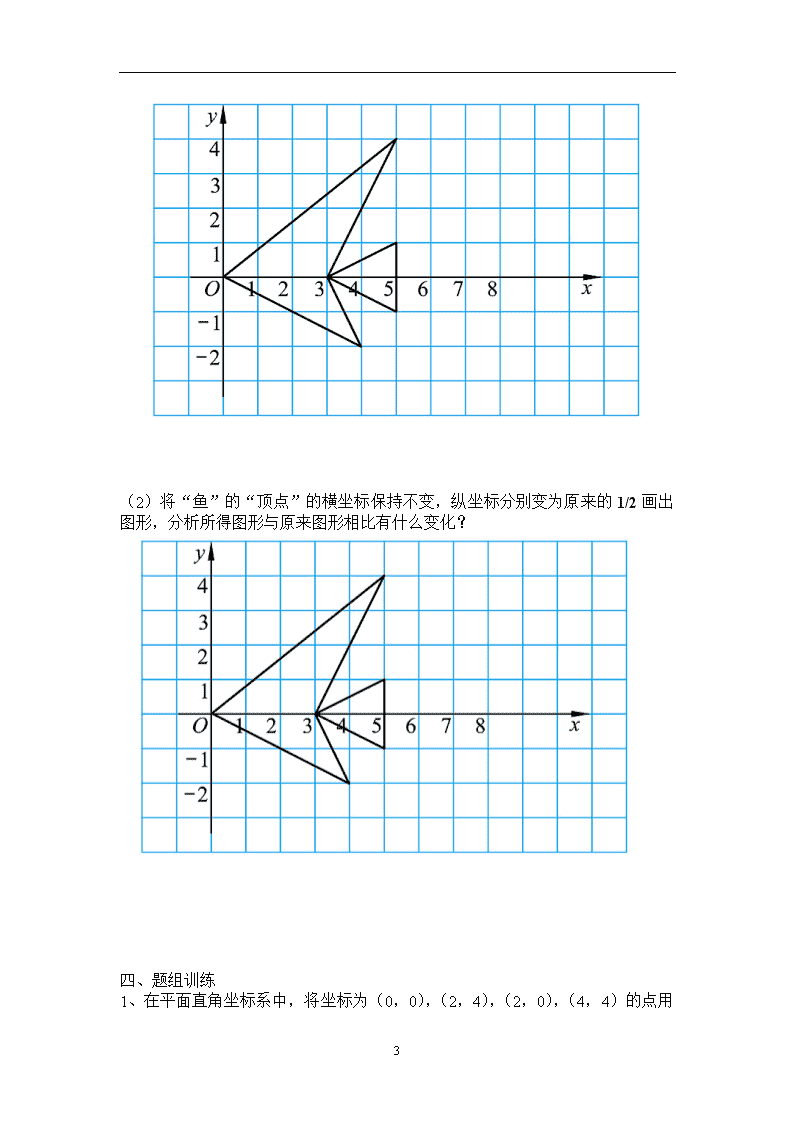
‎ ‎ ‎§5.3变化的“鱼（一）‎ 学习目标：‎ ‎1、在同一直角坐标系中，感受图形上点的坐标变化与图形的变化（平移、轴对称、伸长、压缩）之间的关系并能找出变化规律。‎ ‎2、由坐标的变化探索新旧图形之间的变化。‎ 学习过程：‎ 一、旧知回顾：‎ ‎-2‎ ‎1、平面直角坐标系定义：在平面内，两条____________且有公共_________的数轴组成平面直角坐标系。‎ ‎2、坐标平面内点的坐标的表示方法____________。‎ ‎3、各象限点的坐标的特征：‎ 二、新知检索：‎ ‎1、在方格纸上描出下列各点（0，0），（5，4），（3，0），（5，1），（5，-1），‎ ‎（3，0），（4，-2）， （0，0）并用线段依次连接，观察形成了什么图形 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  y ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  5 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  4‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  3‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  2 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  1‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  ‎ x ‎ ‎ ‎ ‎ ‎ ‎ ‎  O ‎  1‎ ‎  2‎ ‎  3‎ ‎  4‎ ‎  5‎ ‎  6‎ ‎  7‎ ‎  8‎ ‎  9‎ ‎  10‎ ‎  ‎ ‎ ‎ ‎ ‎ ‎  —1‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ —2‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  —3‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎  —4‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 三、典例分析 例1、‎ 4‎ ‎ ‎ ‎（1）将“鱼”的“顶点”的纵坐标保持不变，横坐标分别加5画出图形，分析所得图形与原来图形相比有什么变化？如果纵坐标保持不变，横坐标分别减2呢？‎ ‎（2）将“鱼”的“顶点”的横坐标保持不变，纵坐标分别加3画出图形，分析所得图形与原来图形相比有什么变化？如果横坐标保持不变，纵坐标减2呢？‎ ‎ ‎ 例2、（1）将“鱼”的“顶点”的纵坐标保持不变，横坐标分别变为原来的2倍画出图形，分析所得图形与原来图形相比有什么变化？‎ 4‎ ‎ ‎ ‎（2）将“鱼”的“顶点”的横坐标保持不变，纵坐标分别变为原来的1/2画出图形，分析所得图形与原来图形相比有什么变化？‎ 四、题组训练 4‎ ‎ ‎ ‎1、在平面直角坐标系中，将坐标为（0，0），（2，4），（2，0），（4，4）的点用线段依次连接起来形成一个图案。‎ ‎（1）这四个点的纵坐标保持不变，横坐标变成原来的1/2，将所得的四个点用线段依次连接起来，所得图案与原来图案相比有什么变化？‎ ‎（2）纵、横分别加3呢？‎ ‎（3）纵、横分别变成原来的2倍呢？‎ 归纳：图形坐标变化规律 1、 平移规律：‎ 2、 图形伸长与压缩：‎ 4‎