运用公式法教案

运用公式法教案

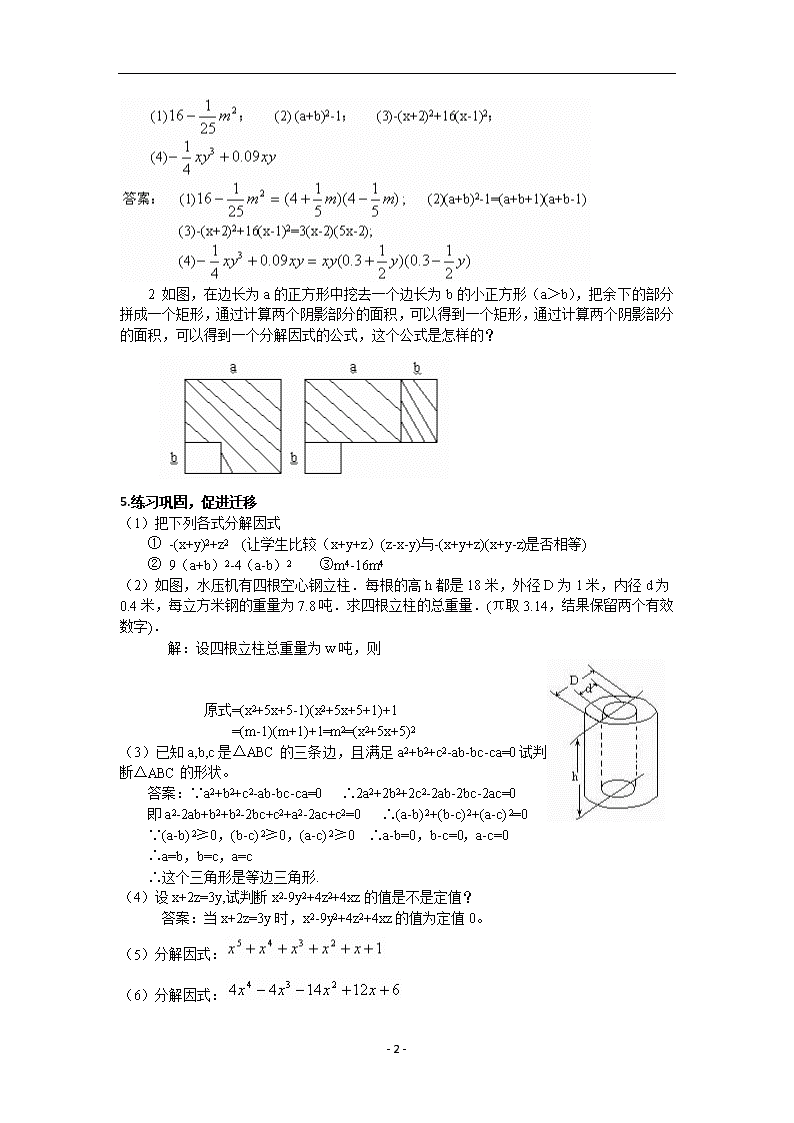
‎4.3 运用公式法 一、教学目标 ‎    1．    经历通过整式乘法的平方差、完全平方公式逆向得出公式法分解因式的方法的过程，发展学生的逆向思维。‎ ‎    2． 会用公式法（直接用公式不出两次）分解因式（指数是正整数）。‎ 二、教学重难点　用公式法（直接用公式不出两次）分解因式（指数是正整数）‎ 三、教学过程设计 第一课时 ‎1.创设情景，导出问题 ‎(1) 观察多项式x2-25，9x2-y2,它们有什么共同特征？‎ ‎（这是对平方差公式的再认识，通过整式乘法的逆变形得到分解因式的方法，让学生进一步感受到整式乘法与分解因式的互逆关系。）‎ ‎(2) 将它们分别写成两个因式的乘积，说明你的理由，并与同伴交流。‎ ‎（让学生充分交流，加深对这种方法的理解。）‎ ‎2.探索交流，概括概念 讨论：‎ ‎（1）多项式的各项都能写成平方的形式。如x2-25中：x2本身是平方的形式，25=52也是平方的形式；9x2-y2也是如此。‎ ‎（2）逆用乘法公式(a+b)(a-b)=a2-b2,‎ 可知x2-25= x2-52=(x+5)(x-5),9x2-y2=(3x)2-y2=(3x+y)(3x-y).‎ 所以我们可以借助乘法公式(a+b)(a-b)=a2-b2的逆过程得到乘法公式a2-b2= (a+b)(a-b)‎ ‎3.巩固应用，拓展研究 例1 把下列各式分解因式：‎ ‎    ‎ ‎（直接利用平方差公式分解因式，让学生体会公式中的a，b在此例中分别是什么）‎ 提问：a2-b2= (a+b)(a-b) 中a，b都表示单项式吗？它们可以是多项式吗？‎ 例2          把下列各式分解因式：‎ ‎(1) 9(m+n)2-(m-n)2; (2) 2x3-8x;‎ 解 (1)9(m+n)2-(m-n)2=4(2m+n)(m+2n) ‎ ‎（进一步让学生理解平方差公式中的字母a，b不仅可以表示数，而且可以表示其他代数式。）‎ ‎(2)2x3-8x=2x(x2-4)=2x(x2-2x)=2x(x+2)(x-2)‎ ‎ （引导学生体会多项式中若含有公因式，就要先提公因式，然后进一步分解，直至不能再分解为止。）‎ ‎4.应用加强，课内深化 ‎ 1 把下列各式分解因式：‎ - 3 -‎ ‎ 2 如图，在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），把余下的部分拼成一个矩形，通过计算两个阴影部分的面积，可以得到一个矩形，通过计算两个阴影部分的面积，可以得到一个分解因式的公式，这个公式是怎样的？‎ ‎          ‎ ‎5.练习巩固，促进迁移 ‎（1）把下列各式分解因式 ‎① -(x+y)2+z2 (让学生比较（x+y+z）(z-x-y)与-(x+y+z)(x+y-z)是否相等) ‎ ‎② 9（a+b）2-4（a-b）2 ③m4-16m4‎ ‎（2）如图，水压机有四根空心钢立柱．每根的高h都是18米，外径D为1米，内径d为0.4米，每立方米钢的重量为7.8吨．求四根立柱的总重量．(π取3.14，结果保留两个有效数字)．‎ 解：设四根立柱总重量为w吨，则 ‎　　‎ ‎　　　=7.8π(D+d)(D-d)h ‎　　　=7.8×3.14×1.4×0.6×18=3.7×102(吨)．‎ ‎　　答：四根立柱总重量约3.7×102吨．‎ ‎6.回顾联系，形成结构 想一想：怎样通过整式乘法的平方差公式逆向用法来分解因式，分解时应注意什么？‎ ‎（通过问题的回答，引导学生自主总结，把分散的知识系统化、结构化，形成知识网络，完善学生的认知结构，加深对所学知识的理解．）‎ ‎7.课外作业与拓展 参见励耘精品系列丛书《课时导航》北师大版八年级（下）P21－P23‎ ‎ ‎ ‎ ‎ 第二课时 ‎1.创设情景，导出问题 把乘法公式 ‎(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,反过来，就得到 a2+2ab+b2=(a+b)2， a2-2ab+b2=(a-b)2‎ 上面这个变化过程是分解因式吗？说明你的理由。‎ ‎2.探索交流，解决问题 答案：a2±2ab+b2=(a±b)2是分解因式。因为(a+b)2是因式的乘积的形式，(a-b)2也是因式的乘积的形式。‎ 形如a2+2ab+b2，a2-2ab+b2的式子称为完全平方式。‎ 由分解因式与整式乘法的关系可以看出，如果把乘法公式反过来，那么就可以用来吧某些多项式分解因式，这种分解因式的方法叫做运用公式法。‎ ‎3.练习巩固，促进迁移 ‎1把下列各式分解因式：‎ ‎ ‎ ‎       (1)x2+14x+49; (2)(m+m)2-6(m+n)+9‎ ‎       (3)3ax2+6axy+3ay2; (4)-x2-4y2+4xy 答案：‎ ‎       (1)x2+14x+49=x2+2×7x+72=(x+7)2‎ ‎       (2)(m+m)2-6(m+n)+9=[(m+n)-3]2=(m+n-3)2‎ ‎       (3)3ax2+6axy+3ay2=3a(x2+2xy+y2)=3a(x+y)2‎ ‎       (4)-x2-4y2+4xy=-(x-2y)2‎ ‎（引导学生对照完全平方公式，确定公式中的a ，b在此例中分别是什么。）‎ ‎2把下列各式分解因式：‎ ‎（引导学生进一步体会若有公因式要先提公因式，然后在进一步分解。）‎ ‎4.课内深化，提升能力 ‎（1）若16x2+24xy+ny2是一个完全平方式，求n的值。‎ ‎（此题改编自励耘精品系列丛书《课时导航》北师大版八年级（下）P23第6题）‎ ‎（2）求证(x+1)(x+2)(x+3)(x+4)+1是一个完全平方式。‎ 证明一：原式=(x2+5x+4)(x2+5x+6)+1‎ ‎=(x2+5x)2+10(x2+5x)+25‎ ‎=(x2+5x+5)2 ∴原命题成立 证明二：原式=[(x+1)(x+4)][(x+2)(x+3)]+1‎ ‎=(x2+5x+4)(x2+5x+6)+1‎ 令a=x2+5x+4，则x2+5x+6=a+2‎ 原式=a(a+2)+1=(a+1)2‎ 即(x+1)(x+2)(x+3)(x+4)+1=(x2+5x+5)2‎ 证明三：原式=(x2+5x+4)(x2+5x+6)+1‎ 令 ‎ 原式=(x2+5x+5-1)(x2+5x+5+1)+1‎ ‎=(m-1)(m+1)+1=m2=(x2+5x+5)2‎ ‎（3）已知a,b,c是△ABC的三条边，且满足a2+b2+c2-ab-bc-ca=0试判断△ABC的形状。‎ 答案：∵a2+b2+c2-ab-bc-ca=0 ∴2a2+2b2+2c2-2ab-2bc-2ac=0‎ 即a2-2ab+b2+b2-2bc+c2+a2-2ac+c2=0 ∴(a-b) 2+(b-c) 2+(a-c) 2=0‎ ‎∵(a-b) 2≥0，(b-c) 2≥0，(a-c) 2≥0 ∴a-b=0，b-c=0，a-c=0‎ ‎∴a=b，b=c，a=c ‎∴这个三角形是等边三角形.‎ ‎（4）设x+2z=3y,试判断x2-9y2+4z2+4xz的值是不是定值？‎ 答案：当x+2z=3y时，x2-9y2+4z2+4xz的值为定值0。‎ ‎（5）分解因式：‎ ‎（6）分解因式：‎ - 3 -‎ ‎5.回顾联系，形成结构 想一想：怎样通过整式乘法的平方差公式逆向用法来分解因式，分解时应注意什么？‎ ‎（通过问题的回答，引导学生自主总结，把分散的知识系统化、结构化，形成知识网络，完善学生的认知结构，加深对所学知识的理解．）‎ ‎6.课外作业与拓展 - 3 -‎