八年级数学上册第2章三角形章末复习课件 湘教版

八年级数学上册第2章三角形章末复习课件 湘教版

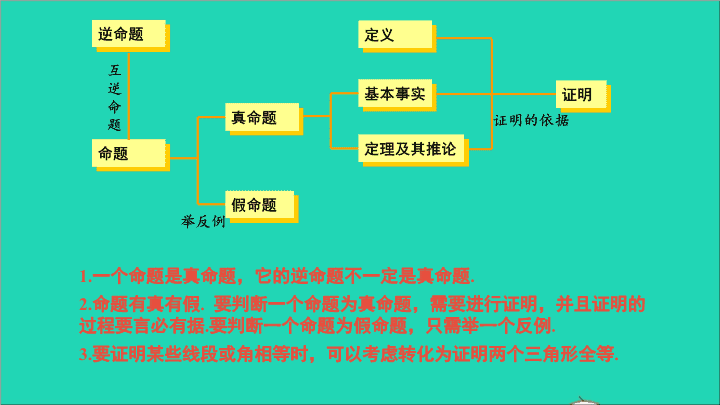
章末复习2 1.一个命题是真命题，它的逆命题不一定是真命题.2.命题有真有假.要判断一个命题为真命题，需要进行证明，并且证明的过程要言必有据.要判断一个命题为假命题，只需举一个反例.3.要证明某些线段或角相等时，可以考虑转化为证明两个三角形全等. 不在同一条直线上的三条线段首尾顺次相接所组成的图形，称为三角形，可以用符号“△”表示；三角形的相关概念顶点是A、B、C的三角形，记作“△ABC”，读作“三角形ABC”. 组成三角形的三条线段叫做三角形的边，即边AB、BC、AC，有时也用a，b，c来表示，顶点A所对的边BC用a表示，边AC、AB分别用b，c来表示.ABCabc 三角形中三边的关系★三角形任意两边之和大于第三边，任意两边之差小于第三边.★三角形的三个内角的和等于180°.三角形内角和定理 三角形的角平分线、中线和高线任意三角形都有三条角平分线，并且它们相交于三角形内一点；三角形有三条中线，它们相交于三角形内一点；任意三角形都有三条高线，它们所在的直线相交于一点. 全等三角形能够完全重合的两个三角形是全等三角形，用符号“≌”连接，读作“全等于”；用“≌”连接的两个全等三角形，表示对应顶点的字母写在对应的位置上；全等三角形的性质：全等三角形的对应边、对应角相等. 全等三角形的判定A′B′C′ABC三边对应相等的两个三角形全等，简写为“边边边”或“SSS”；两角和它们的夹边对应相等的两个三角形全等，简写为“角边角”或“ASA”； 两角和其中一角的对边对应相等的两个三角形全等，简写为“角角边”或“AAS”；两边和它们的夹角对应相等的两个三角形全等，简写为“边角边”或“SAS”.A′B′C′ABC 作三角形熟练以下三种三角形的作法及依据.①已知三角形的两边及其夹角，作三角形；abα ②已知三角形的两角及其夹边，作三角形；βaα ③已知三角形的三边，作三角形.abc 随堂练习1.下列各组长度的线段为边，能构成三角形的是（）A.7cm、5cm、12cmB.6cm、8cm、15cmC.8cm、4cm、3cmD.4cm、6cm、5cm.D 2.如图，△AOB≌△COD，A和C，B和D是对应顶点，若BO=8，AO=5，AB=10，则CD的长为（）A.10B.8C.5D.不能确定A 3.如图，已知∠1=∠2，要说明△ABD≌△ACD，还需从下列条件中选一个，错误的选法是（）A.∠ADB=∠ADCB.∠B=∠CC.DB=DCD.AB=ACC 4.已知三角形的两边及其夹角，求作这个三角形．已知：线段a，c，∠α.求作：△ABC，使BC=a，AB=c，∠ABC=∠α.ac 作法示范（1）作一条线段BC=a；（2）以B为顶点，以BC为边作；BCBCBCBC（3）在射线BD上截取线段BA=c；（4）连接AC．△ABC就是所求作的三角形．ADD 5.已知一个三角形的两边长分别是2cm和4cm，则第三边长x的取值范围是___________;若x是奇数，则x的值是___________;此三角形的周长p的取值范围是＿＿＿＿＿＿.2

查看更多