八年级下数学课件相似三角形的性质_鲁教版

八年级下数学课件相似三角形的性质_鲁教版

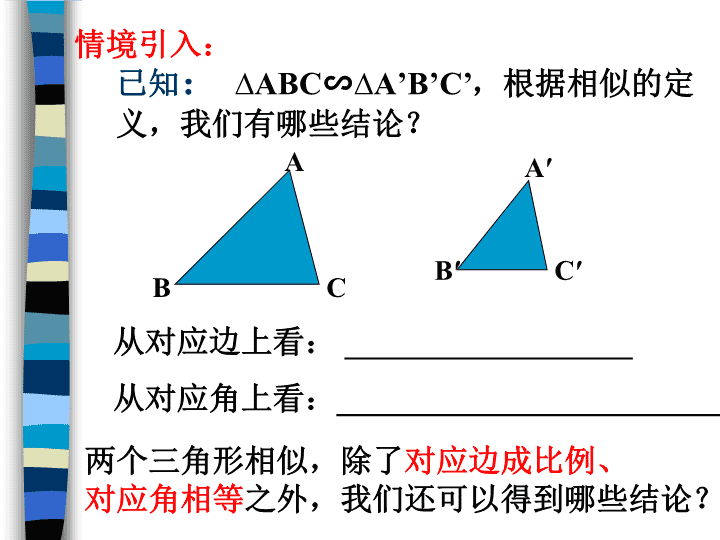
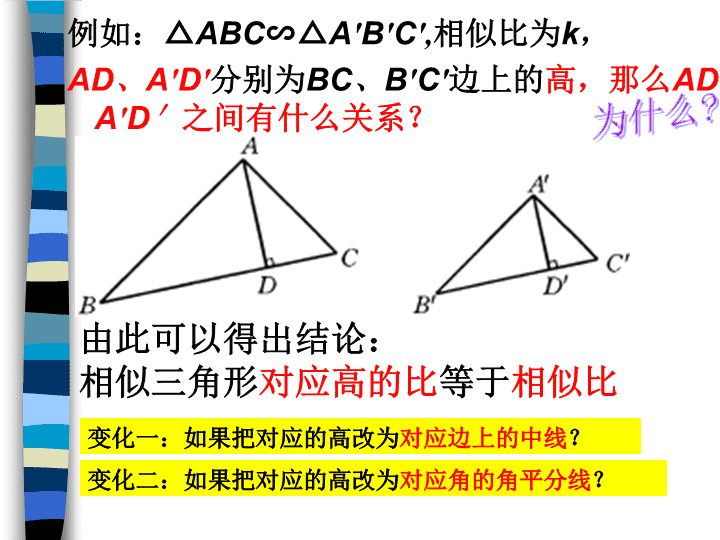
相似三角形的性质 已知：∆ABC∽∆A’B’C’，根据相似的定义，我们有哪些结论？情境引入：ACBB′A′C′从对应边上看：__________________从对应角上看：____________________________两个三角形相似，除了对应边成比例、对应角相等之外，我们还可以得到哪些结论？ 例如：△ABC∽△A′B′C′,相似比为k，AD、A′D′分别为BC、B′C′边上的高，那么AD、A′D′之间有什么关系？由此可以得出结论：相似三角形对应高的比等于相似比变化一：如果把对应的高改为对应边上的中线？变化二：如果把对应的高改为对应角的角平分线？为什么? 我们再用心来观察下面一组图形：图中(1)(2)(3)分别是边长为1、2、3的等边三角形，它们都相似？为什么？（2）与（1）的相似比＝________________，（2）与（1）的周长比＝________________;（2）与（1）的面积比＝________________;（3）与（1）的相似比＝________________，（3）与（1）的周长比＝________________.（3）与（1）的面积比＝________________.(1)(2)(3) 由此可以得出结论：相似三角形的周长比等于_____________．由可以得出结论：相似三角形的面积比等于___________． 我来试一试：1.相似三角形对应边的比为3∶5,那么相似比为___________,对应角的角平分线的比为______,周长的比为_____,面积的比为_____。变化：相似三角形对应边的比为9∶8？相似三角形对应边的比为0.5? 我来试一试：2．两个相似三角形对应高的比为2:5，则对应角平分线的比为____,周长比为___.3．两个相似三角形对应中线的比为1:4，则对应高的比为______,面积比为______。 例题：已知：，它们的周长分别为60cm和72cm，且AB=15cm，∽△△=24cm。求：BC,AC,A′B′,A′C′ABC 1、如图，点D、E分别是△ABC边AB、AC上的点，且DE∥BC，BD＝2AD，那么△ADE的周长︰△ABC的周长＝。ABCDE展示风采： 例2：如图所示，D、E分别是AC、AB上的点，.已知△ABC的面积为100cm2，求四边形BCDE的面积。AEBDC解：∵，∠A=∠A∴∽△△(两边对应成比例,且夹角相等,两三角形相似)∴（相似三角形面积的比等于相似比的平方）(以下解略)22ACAESSABCADE=DD 展示风采：1、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.2、两个相似三角形对应的中线长分别是6cm和18cm，若较大三角形的周长是42cm，面积是12，则较小三角形的周长____cm,面积为____。1:21:42cm2cm 课堂小结：今天我们学习相似三角形哪些性质？1.相似三角形对应高的比等于相似比,相似三角形对应中线的比等于相似比,相似三角形对应角平分线的比等于相似比。2.相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方。 1.已知：如图△ABC中，DE∥BC，AF⊥DE垂足为F，AF交BC于G。若AF=5，FG=3，则AFEDBCGHNMFEDCBA2、如图在ABCD中，E是BC的中点，F是BE的中点，AE与DF交于点H，过点H作MN⊥AD，垂足为M，交BC于N，则NH:MH=______。再攀高峰。，，===DDABCADESSBCDEAGAF