八年级下数学课件八年级下册数学课件《勾股定理》 人教新课标 (10)_人教新课标

八年级下数学课件八年级下册数学课件《勾股定理》 人教新课标 (10)_人教新课标

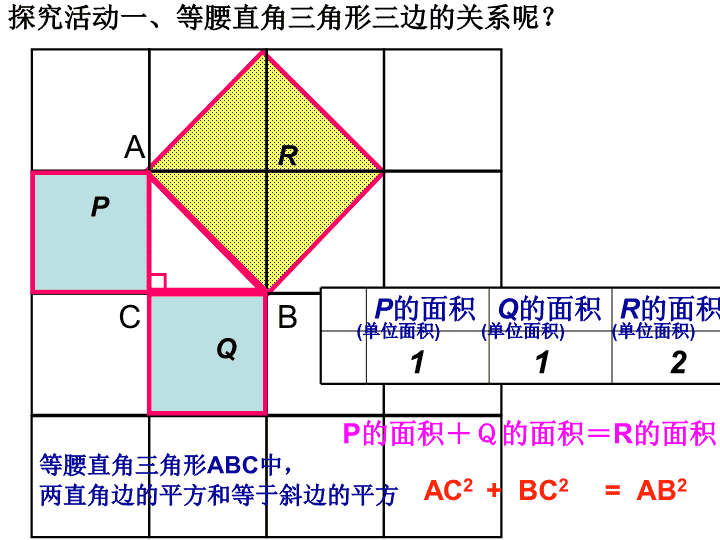
勾股定理CBA 学习目标：1.探究揭示直角三角形三边关系的勾股定理。2.证明勾股定理的正确性。3.会运用勾股定理解决一些简单的实际问题。 PQRP的面积Q的面积R的面积等腰直角三角形ABC中，两直角边的平方和等于斜边的平方探究活动一、等腰直角三角形三边的关系呢？(单位面积)(单位面积)(单位面积)ACB112P的面积＋Ｑ的面积＝R的面积AC2+BC2=AB2 PQRacbSP+SQ=SR猜想:两直角边a、b与斜边c之间的关系？a2+b2=c2探究活动二:对于一般直角三角形三边关系的探索： PQCR如图，小方格的边长为1.(1)你能求出正方形R的面积吗？用了“补”的方法PQCR用了“割”的方法Q 如图：已知四个全等的直角三角形的两直角边长分别为a和b，斜边长为c。利用这些直角三角形拼成一个大的正方形，来说明：babababacccc试一试 cabcabcabcab∵c2==b2-2ab+a2+2ab=a2+b2∴a2+b2=c2大正方形的面积可以表示为；也可以表示为c2该图2002年8月在北京召开的国际数学家大会的会标示意图，取材于我国古代数学著作《勾股圆方图》。证明1： cabcabcabcab∵(a+b)2=a2+2ab+b2=2ab+c2∴a2+b2=c2大正方形的面积可以表示为；也可以表示为(a+b)2C2证明2：C2 勾股定理(毕达哥拉斯定理)（gou－gutheorem）如果直角三角形两直角边分别为a，b，斜边为c，那么即直角三角形两直角边的平方和等于斜边的平方.ac勾弦b股 两千多年前，古希腊有个哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派，1955勾股世界国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。 练习1、求出下列直角三角形中未知边的长度∟∟①②勾股定理 比一比看看谁算得快！2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x做一做1234x=13c １、如图,一个高3米,宽4米的大门,需在相对角的顶点间加一个加固木条,则木条的长为()A.3米B.4米C.5米D.6米C３４2.直角三角形的两边长分别为3、4， 例1如图所示，为了求出湖两岸的A、B两点间的距离，一个观测者在点C设桩，使三角形ABC恰好为直角三角形．通过测量，得到AC的长为160米，BC长为128米．问从点A穿过湖到点B有多远？答：从点A穿过湖到点B有96米。解：在直角三角形ABC中，AC=160米，BC=128米，根据勾股定理可得 9米在台风“麦莎”的袭击中，一棵大树在离地面9米处断裂，树的顶部落在离树根底部12米处。这棵树折断之前有多高？12米例215米 美国第二十任总统伽菲尔德总统巧证勾股定理S梯形=(a+b)(a+b)=(a2+b2)+abS梯形=c2+2·ab=c2+ab即：在Rt△ABC中，∠C=90°c2=a2+b2 11美丽的勾股树 练习2、求出下列直角三角形中未知边的长度∟∟①②勾股定理 课堂练习1、求下列直角三角形中未知边x的长158x=17x2524=768x=10412x=1353 如图，要登上8米高的建筑物BC，为了安全需要，需使梯子底端离建筑物距离AB为6米，问至少需要多长的梯子？8mBCA6m解：在Rt△ABC中∠ABC=90゜,BC=8，AB=6∴AC2=62+82=36+64=100∴AC=10答：梯子至少长10米。 PQC图乙2.观察图乙，小方格的边长为1.91625SP+SQ=SR112图甲图乙P的面积Q的面积R的面积RQPRSP+SQ=SR图甲“割”“补” QPR图甲图乙P的面积Q的面积R的面积112SP+SQ=SRC图甲1.观察图甲，小方格的边长为1.⑴正方形A、B、C的面积各为多少？⑵正方形P、Q、R的面积有什么关系？ PQ图乙2.观察图乙，小方格的边长为1.91625SP+SQ=SR448PQRSP+SQ=SR图甲图甲图乙P的面积Q的面积R的面积acabcRb3.猜想a、b、c之间的关系？a2+b2=c2 .在Rt△ABC中，∠Ｃ=90°已知：a=40，c=41，求b已知:a:b=3:4,c=15,求a、b.(1)在直角三角形中,已知两边,可求第三边;(2)可用勾股定理建立方程.方法小结abcCAB 例题2:如图，将长为5米的梯子AC斜靠在墙上，BC长为2米，求梯子上端A到墙的底端B的距离AB.解:在Rt△ABC中∠ABC=90゜,BC=2,CA=5,根据勾股定理得=（米） 如图，一根电线杆在离地面5米处断裂，电线杆顶部落在离电线杆底部12米处，电线杆折断之前有多高？∴电线杆折断之前的高度=BC+AB=5米+１３米＝１８米5米BAC12米解：∵ＢＣ⊥ＡC，∴在Ｒt△ＡＢＣ中，ＡＣ＝１２，ＢＣ＝５,根据勾股定理， ２、湖的两端有A、Ｂ两点，从与ＢA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为()ABCA.50米B.120米C.100米D.130米130120?A （1）本节课你学到了什么新知识?（2）勾股定理只能用在什么形中？它可以用来解决什么问题？（3）请说出勾股定理得表达式？课堂小结勾股定理 勾股定理1.已知△ＡＢＣ中，∠B＝90°，AC＝13cm，ＢＣ＝5cm,求ＡＢ的长．2.已知等腰直角三角形斜边的长为2cm，求这个三角形的直角边． 两千多年前，古希腊有个哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派，1955勾股世界国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。 邮票赏析这是1955年希腊曾经发行的纪念一位数学家的邮票。 2002年世界数学家大会会标 1.求下列图中表示边的未知数x、y、z的值.①81144②③做一做625576144169xyz 勾股定理的证明方法证法一证法二证法三（邹元治证明）（赵爽证明）赵爽:我国古代数学家走进数学史延伸阅读 勾股定理的证明方法证法四证法五证法六（加菲尔德证明）加菲尔德:第二十任总统（梅文鼎证明）梅文鼎:清代天文、数学家（项明达证明）项明达:清代数学家走进数学史 勾股定理的证明勾股定理是几何学中的明珠，所以它充满魅力，千百年来，人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者，有普通的老百姓，也有尊贵的政要权贵，甚至有国家总统。也许是因为勾股定理既重要又简单，更容易吸引人，才使它成百次地反复被人炒作，反复被人论证。有资料表明，关于勾股定理的证明方法已有500余种，仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。在这数百种证明方法中，有的十分精彩，有的十分简洁，有的因为证明者身份的特殊而非常著名。现在在网络上看到较多的是16种,包括前面的6种,还有:欧几里得证明、利用相似三角形性质证明、杨作玫证明、李锐证明、利用切割线定理证明、利用多列米定理证明、作直角三角形的内切圆证明、利用反证法证明、辛卜松证明、陈杰证明。走进数学史 再见 美国第二十任总统伽菲尔德总统巧证勾股定理aabbccADCBE返回 如图，一根电线杆在离地面5米处断裂，电线杆顶部落在离电线杆底部12米处，电线杆折断之前有多高？5米BAC12米一、情景引入电线杆折断之前的高度=BC+AB=5米+AB的长 1、求出下列直角三角形中未知边的长度。6x25248X试一试: 2、在△ABC中,∠C=90°，∠A、∠B、∠C的对边分别为a、b、c,⑴若a=3，b=4，则c=＿＿；⑵若a=5,c=13,则b=＿＿；⑶若b=8，c=17，则a=＿＿；⑷若a=7,b=24,则c=＿＿.5121525abcCBA 分别以5cm、12cm为直角三角形的直角边作出一个直角三角形ABC，测量斜边的长度，然后验证上述关系对这个直角三角形是否成立。做一做13512ABC .如图，小方格都是边长为1的正方形，求四边形ABCD的面积与周长.EFGH现学现用： 假期中，王强和同学到某海岛上去玩探宝游戏，按照探宝图，他们登陆后先往东走8千米，又往北走2千米，遇到障碍后又往西走3千米，在折向北走到6千米处往东一拐，仅走1千米就找到宝藏，问登陆点A到宝藏埋藏点B的距离是多少千米？AB82361 图甲图乙A的面积B的面积C的面积448ABCSA+SB=SCC图甲1.观察图甲，小方格的边长为1.⑴正方形A、B、C的面积各为多少？⑵正方形A、B、C的面积有什么关系？ ABCC图乙2.观察图乙，小方格的边长为1.⑴正方形A、B、C的面积各为多少？91625SA+SB=SC⑵正方形A、B、C的面积有什么关系？448ABCSA+SB=SC图甲图甲图乙A的面积B的面积C的面积 ABC图乙2.观察图乙，小方格的边长为1.91625SA+SB=SC⑵正方形A、B、C的面积有什么关系？448ABCSA+SB=SC图甲图甲图乙A的面积B的面积C的面积abcabc 图甲图乙A的面积B的面积C的面积448ABCSA+SB=SCC图甲1.观察图甲，小方格的边长为1.⑴正方形A、B、C的面积各为多少？⑵正方形A、B、C的面积有什么关系？ ABC图乙2.观察图乙，小方格的边长为1.91625SA+SB=SC⑵正方形A、B、C的面积有什么关系？448ABCSA+SB=SC图甲图甲图乙A的面积B的面积C的面积abcabc ABCC图乙SA+SB=SCSA+SB=SC图甲abcabc3.猜想a、b、c之间的关系？a2+b2=c2