2019年春八年级数学下册第十九章一次函数19-1函数19-1-1变量与函数课件

2019年春八年级数学下册第十九章一次函数19-1函数19-1-1变量与函数课件

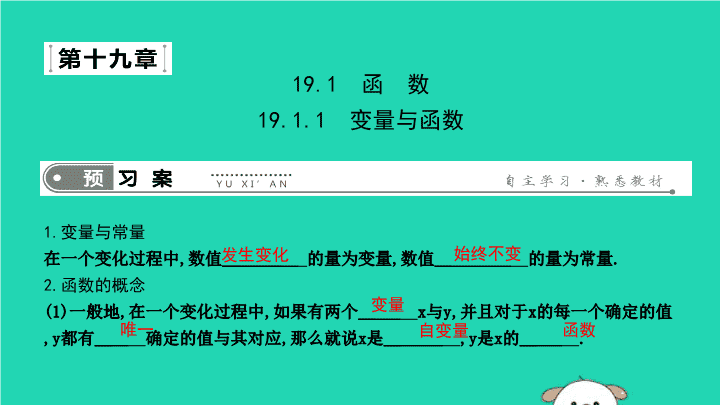
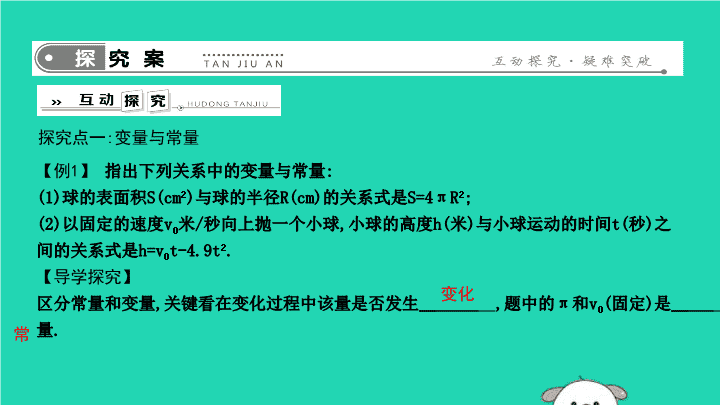
19.1　函　数19.1.1　变量与函数1.变量与常量在一个变化过程中,数值的量为变量,数值的量为常量.2.函数的概念(1)一般地,在一个变化过程中,如果有两个x与y,并且对于x的每一个确定的值,y都有确定的值与其对应,那么就说x是,y是x的.发生变化始终不变变量唯一自变量函数 (2)如果当x=a时,y=b,那么b叫做当自变量的值为a时的.3.函数的解析式用关于的数学式子表示函数与自变量之间的关系,是描述函数的常用方法,这种式子叫做函数的解析式.函数值自变量 探究点一:变量与常量【例1】指出下列关系中的变量与常量:(1)球的表面积S(cm2)与球的半径R(cm)的关系式是S=4πR2;(2)以固定的速度v0米/秒向上抛一个小球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=v0t-4.9t2.【导学探究】区分常量和变量,关键看在变化过程中该量是否发生,题中的π和v0(固定)是量.变化常 解:(1)关系式S=4πR2中,常量是4π,变量是S,R.(2)关系式h=v0t-4.9t2中,常量是v0,4.9,变量是h,t. 探究点二:自变量的取值范围x≥-2且x≠0≥x≠0 【例3】为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成表格:探究点三:函数的解析式及函数值汽车行驶时间t(h)0123…油箱剩余油量Q(L)100948882… 解:(1)Q=100-6t.(2)当t=5时,可得Q=100-6×5=100-30=70(L).答:汽车行驶5h后,油箱中的剩余油量是70L.(3)当Q=55时,可得55=100-6t,解得t=7.5.答:汽车行驶了7.5h.(1)根据表中的数据,写出用t表示Q的解析式;(2)汽车行驶5h后,油箱中的剩余油量是多少?(3)若汽车油箱中剩余油量为55L,则汽车行驶了多少小时?【导学探究】1.由题意知,开始油箱中的油量为L,每行驶1小时,油量减少L.2.利用(1)的解析式,求当t=5时,的值.3.利用(1)的解析式,求当Q=55时,的值.1006Qt 1.对于圆的周长公式C=2πR,下列说法错误的是()(A)π是变量(B)R,C是变量(C)R是自变量(D)2是常量AC3.(2018鄄城期中)某地海拔高度h与温度T的关系可用T=21-6h来表示(其中温度单位:℃,海拔高度单位:千米),则该地区某海拔高度为2000米的山顶上的温度为()(A)15℃(B)9℃(C)3℃(D)7℃B 4.汽车由A地驶往相距120km的B地,已知它的平均速度是30km/h,则汽车距B地路程s(km)与行驶时间t(h)的函数解析式是,自变量t的取值范围是.s=120-30t0≤t≤45.(2018平阴期末)将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm. (1)根据题意,将下面的表格补充完整.解:(1)根据题意,完成表格如下:白纸张数x(张)12345…纸条总长度y(cm)205471…白纸张数x(张)12345…纸条总长度y(cm)2037547188… (2)求出y与x的函数解析式.(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?解:(2)由题意知将长为20cm的长方形白纸粘合起来,粘合部分的宽为3cm,x张白纸粘合,纸条总长度y=(20-3)x+3=17x+3.(3)1656÷8=207(cm),当y=207时,17x+3=207,解得x=12,所以需要12张这样的白纸.