八年级数学上册第14章全等三角形14-2三角形全等的判定（第5课时）课件（新版）沪科版

八年级数学上册第14章全等三角形14-2三角形全等的判定（第5课时）课件（新版）沪科版

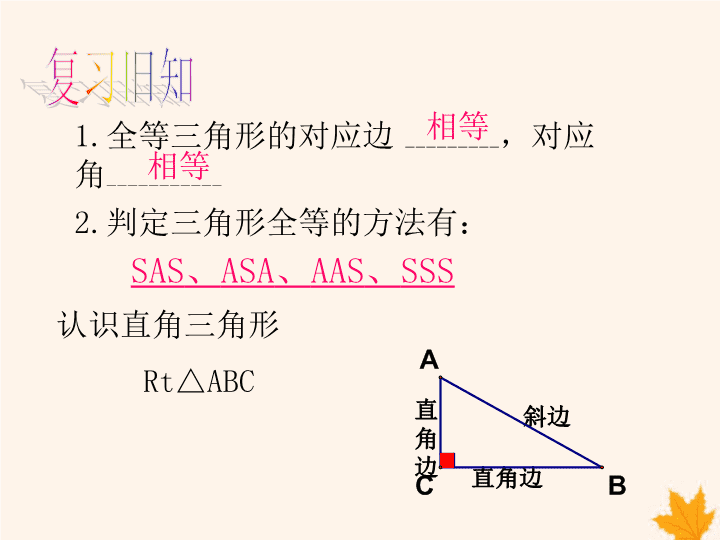
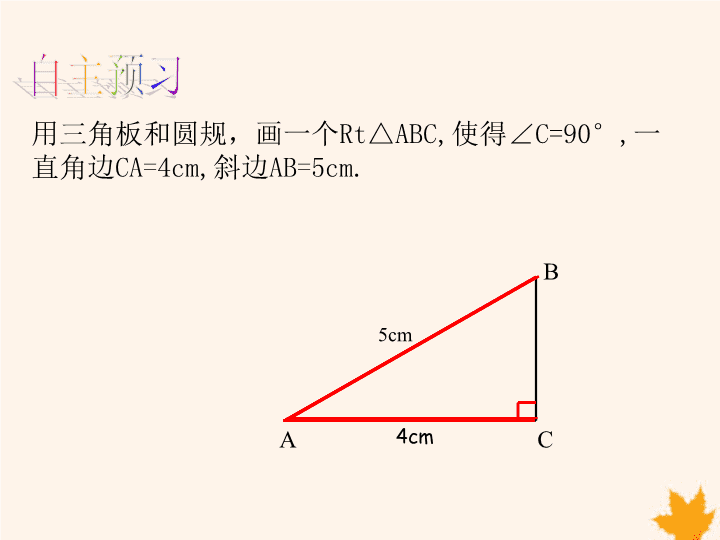
14.2三角形全等的判定第五课时第十四章 1.全等三角形的对应边---------，对应角-----------相等相等2.判定三角形全等的方法有：SAS、ASA、AAS、SSS直角边直角边斜边认识直角三角形Rt△ABC复习旧知 用三角板和圆规，画一个Rt△ABC,使得∠C=90°,一直角边CA=4cm,斜边AB=5cm.ABC5cm4cm自主预习 1.画∠MCN=90°;CNM自主预习 1.画∠MCN=90°;CNM2.在射线CM上截取CA=4cm;A自主预习 1.画∠MCN=90°;2.在射线CM上截取CA=4cm;3.以A为圆心，5cm为半径画弧，交射线CN于B;CNMAB自主预习 1.画∠MCN=90°;CNM2.在射线CM上截取CA=4cm;B3.以A为圆心，5cm为半径画弧，交射线CN于B;A4.连接AB;△ABC即为所要画的三角形自主预习 把我们刚画好的直角三角形剪下来，和同桌的比比看，这些直角三角形有怎样的关系呢？自主预习 Rt△ABC≌ABC5cm4cmA′B′C′5cm4cm你发现了什么？Rt△A′B′C′ 斜边、直角边定理斜边和一条直角边分别相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”前提条件1条件2 斜边、直角边定理(HL)ABCA′B′C′∴在Rt△ABC和Rt△A′B′C′中AB=A′B′BC=B′C′∴Rt△ABC≌Rt△A′B′C′∵∠C=∠C′=90°有斜边和一条直角边对应相等的两个直角三角形全等.前提条件1条件2 满足下列条件的两个三角形是否全等?为什么?1.一个锐角及这个锐角的对边对应相等的两个直角三角形.全等(AAS)判断 2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.全等满足下列条件的两个三角形是否全等?为什么?(ASA)判断 3.两直角边对应相等的两个直角三角形.全等满足下列条件的两个三角形是否全等?为什么?(SAS)判断 4.有两边对应相等的两个直角三角形.全等满足下列条件的两个三角形是否全等?为什么?情况1：全等情况2：全等(SAS)(HL)判断 例7已知：如图,已知:∠BAC=∠CDB=90°,AC=DB求证：AB=DCCAD证明：∵∠BAC=∠CDB=90°,∴△ABC、△BCD都是直角三角形又∵AC=DBBC=CB∴Rt△ABC≌Rt△BAD(HL)B∴AB=DC探究新知 课堂小结本节课你学习了哪些知识？斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边”或“HL” 已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF,求证：△ABC≌△DEFABCPDEFQ变式1：若把∠BAC＝∠EDF,改为BC＝EF，△ABC与△DEF全等吗？请说明思路。随堂练习 已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF,求证：△ABC≌△DEFABCPDEFQ变式2：若把∠BAC＝∠EDF,改为AC=DF，△ABC与△DEF全等吗？请说明思路。随堂练习 已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF,求证：△ABC≌△DEFABCPDEFQ变式3：请你把例题中的∠BAC＝∠EDF改为另一个适当条件，使△ABC与△DEF仍能全等。试证明。随堂练习 直角三角形全等的判定一般三角形全等的判定“SAS”“ASA”“AAS”“SSS”“SAS”“ASA”“AAS”“HL”灵活运用各种方法证明直角三角形全等“SSS”方法总结 已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.求证:△ABC是等腰三角形.DBCAFE随堂练习