2019-2020学年山东省济南市济阳区七年级下学期期末数学试卷

2019-2020学年山东省济南市济阳区七年级下学期期末数学试卷

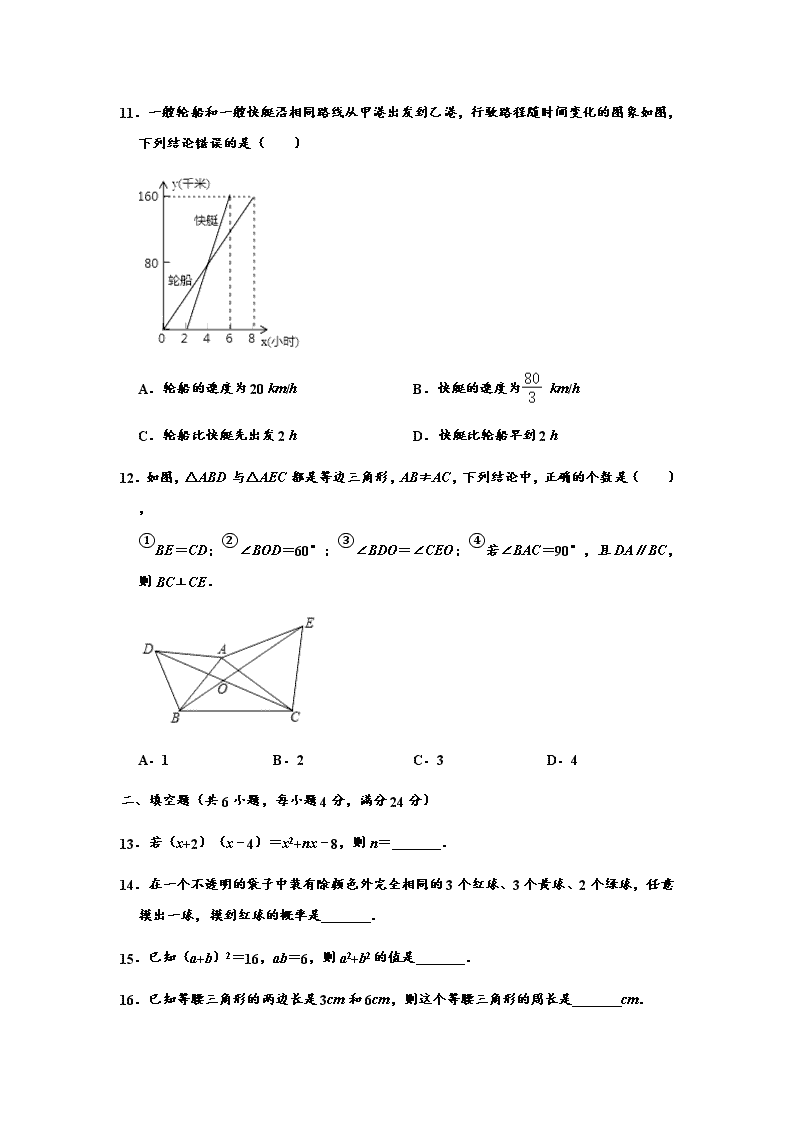
‎2019-2020学年山东省济南市济阳区七年级第二学期期末数学试卷 一、选择题 ‎1．在下列四个交通标志图中，是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎2．下列计算正确的是（　　）‎ A．x3•x3＝x6 B．a8÷a4＝a2 C．（x3）3＝x6 D．a3+a4＝a7‎ ‎3．2015年4月，生物学家发现一种病毒的长度约为0.0000043米，利用科学记数法表示为（　　）‎ A．4.3×106米 B．4.3×10﹣5米 C．4.3×10﹣6米 D．43×107米 ‎4．如图，已知a、b、c、d四条直线，a∥b，c∥d，∠1＝112°，则∠2等于（　　）‎ A．58° B．68° C．78° D．112°‎ ‎5．如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC＝100°，则∠BOE的大小为（　　）‎ A．100° B．110° C．120° D．130°‎ ‎6．如图，点E，F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加的一个条件是（　　）‎ A．∠A＝∠C B．∠D＝∠B C．AD∥BC D．DF∥BE ‎7．某同学带100元钱去买书，已知每册定价8.2元，买书后余下的钱y元和买的册数x之间的函数关系式是（　　）‎ A．y＝8.2x B．y＝100﹣8.2x C．y＝8.2x﹣100 D．y＝100+8.2x ‎8．一个三角形的两边长分别为2cm和5cm，则此三角形第三边长可能是（　　）‎ A．2cm B．3cm C．5cm D．8cm ‎9．如图所示，已知AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D，则∠DBC的度数（　　）‎ A．40° B．70° C．30° D．50°‎ ‎10．如果小球在如图所示的地面上自由滚动，并随机停留在某块方砖上，那么它最终停留在黑色区域的概率是（　　）‎ A． B． C． D．‎ ‎11．一艘轮船和一艘快艇沿相同路线从甲港出发到乙港，行驶路程随时间变化的图象如图，下列结论错误的是（　　）‎ A．轮船的速度为20 km/h B．快艇的速度为 km/h ‎ C．轮船比快艇先出发2 h D．快艇比轮船早到2 h ‎12．如图，△ABD与△AEC都是等边三角形，AB≠AC，下列结论中，正确的个数是（　　），‎ ‎①BE＝CD；②∠BOD＝60°；③∠BDO＝∠CEO；④若∠BAC＝90°，且DA∥BC，则BC⊥CE．‎ A．1 B．2 C．3 D．4‎ 二、填空题（共6小题，每小题4分，满分24分）‎ ‎13．若（x+2）（x﹣4）＝x2+nx﹣8，则n＝　 　．‎ ‎14．在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球，任意摸出一球，摸到红球的概率是　 　．‎ ‎15．已知（a+b）2＝16，ab＝6，则a2+b2的值是　 　．‎ ‎16．已知等腰三角形的两边长是3cm和6cm，则这个等腰三角形的周长是　 　cm．‎ ‎17．暑假里，小明爸爸开车带小明去青岛游玩，一路上匀速前行，小明记下了如下数据：‎ 观察时刻 ‎8：00‎ ‎8：06‎ ‎8：18‎ ‎（注：“青岛80km”表示离青岛的距离为80km）‎ 路牌内容 青岛80km 青岛70km 青岛50km 从8点开始，记汽车行驶的时间为t（min），汽车离青岛的距离为s（km），则s与t的关系式为　 　．‎ ‎18．如图，△ABE和△ACD是△ABC分别以AB、AC为对称轴翻折180°形成的，若∠1：∠2：∠3＝29：4：3，则∠α的度数为　 　．‎ 三、解答题（共9小题，满分78分，解答应写出必要的文字说明，证明过程或演算步骤）‎ ‎19．计算：‎ ‎（1）﹣12019﹣（）﹣2﹣（3.14﹣π）0‎ ‎（2）（ab3﹣2a2b2）÷ab+（a+b）•2a ‎20．先化简，再求值：（x﹣2y）2﹣（x+y）（x﹣y）﹣5y2，其中x＝，y＝﹣2‎ ‎21．如图，EF∥AD，∠BEF＝∠ADG，∠BAC＝80°，求∠AGD的度数．‎ ‎22．如图，点B、F、C、E在同一条直线上，FB＝CE，AC∥DF，AC＝DF．求证：AB＝‎ DE．‎ ‎23．下面的方格图是由边长为1的42个小正方形拼成的，△ABC的顶点A、B、C均在小正方形的顶点上．‎ ‎（1）作出△ABC关于直线m对称的△A′B′C′；‎ ‎（2）求△ABC的面积．‎ ‎24．元旦期间，某超市开展有奖促销活动，凡在超市购物的顾客均有转动圆盘的机会（如图），如果规定当圆盘停下来时指针指向8就中一等奖，指向2或6就中二等奖，指向1或3或5就中纪念奖，指向其余数字不中奖．‎ ‎（1）转动转盘中奖的概率是多少？‎ ‎（2）元旦期间有1000人参与这项活动，估计获得一等奖的人数是多少？‎ ‎25．为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：‎ 汽车行驶时间t（h）‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ 油箱剩余油量Q（L）‎ ‎100‎ ‎94‎ ‎88‎ ‎82‎ ‎…‎ ‎（1）根据上表的数据，请你写出Q与t的关系式；‎ ‎（2）汽车行驶5h后，油箱中的剩余油量是多少？‎ ‎（3）该品牌汽车的油箱加50L，若以100km/h的速度匀速行驶，该车最多能行驶多远？‎ ‎26．如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，点D是射线BC上一动点，过点B作BE⊥AD，垂足为点E，交直线AC于点P．‎ ‎（1）如图（1），若点D在BC的延长线上，且点E在线段AD上，试猜想AP，CD，BC之间的数最关系，并说明理由；‎ ‎（2）如图（2），若点D在线段BC上，试猜想AP，CD，BC之间的数量关系，并说明理由．‎ ‎27．如图，在长方形ABCD中，AB＝8cm，BC＝12cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒．‎ ‎（1）如图1，S△DCP＝　 　．（用t的代数式表示）‎ ‎（2）如图1，当t＝3时，试说明：△ABP≌△DCP．‎ ‎（3）如图2，当点P从点B开始运动的同时，点Q从点C出发，以vcm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．‎ 参考答案 一、选择题（本大题共12个小题，每小题4分，共48分）‎ ‎1．在下列四个交通标志图中，是轴对称图形的是（　　）‎ A． B． C． D．‎ 解：“如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形”，符合这一要求的只有B．‎ 故选：B．‎ ‎2．下列计算正确的是（　　）‎ A．x3•x3＝x6 B．a8÷a4＝a2 C．（x3）3＝x6 D．a3+a4＝a7‎ 解：A、x3•x3＝x6，正确；‎ B、a8÷a4＝a4，故此选项错误；‎ C、（x3）3＝x9，故此选项错误；‎ D、a3+a4，无法合并，故此选项错误；‎ 故选：A．‎ ‎3．2015年4月，生物学家发现一种病毒的长度约为0.0000043米，利用科学记数法表示为（　　）‎ A．4.3×106米 B．4.3×10﹣5米 C．4.3×10﹣6米 D．43×107米 解：0.0000043＝4.3×10﹣6，‎ 故选：C．‎ ‎4．如图，已知a、b、c、d四条直线，a∥b，c∥d，∠1＝112°，则∠2等于（　　）‎ A．58° B．68° C．78° D．112°‎ 解：∵a∥b，c∥d，‎ ‎∴∠3＝∠1，∠4＝∠3，‎ ‎∴∠1＝∠4＝112°，‎ ‎∴∠2＝180°﹣∠4＝68°，‎ 故选：B．‎ ‎5．如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC＝100°，则∠BOE的大小为（　　）‎ A．100° B．110° C．120° D．130°‎ 解：∵OA平分∠EOC，∠EOC＝100°，‎ ‎∴∠AOE＝∠EOC＝50°，‎ ‎∴∠BOE＝180°﹣∠AOE＝130°．‎ 故选：D．‎ ‎6．如图，点E，F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加的一个条件是（　　）‎ A．∠A＝∠C B．∠D＝∠B C．AD∥BC D．DF∥BE 解：当∠D＝∠B时，‎ 在△ADF和△CBE中 ‎∵，‎ ‎∴△ADF≌△CBE（SAS），‎ 故选：B．‎ ‎7．某同学带100元钱去买书，已知每册定价8.2元，买书后余下的钱y元和买的册数x之间的函数关系式是（　　）‎ A．y＝8.2x B．y＝100﹣8.2x C．y＝8.2x﹣100 D．y＝100+8.2x 解：∵x册书用8.2x元钱，‎ ‎∴剩余钱数y＝100﹣8.2x，‎ 故选：B．‎ ‎8．一个三角形的两边长分别为2cm和5cm，则此三角形第三边长可能是（　　）‎ A．2cm B．3cm C．5cm D．8cm 解：设第三边长为xcm，‎ 则5﹣2＜x＜5+2，‎ ‎3＜x＜7，‎ 故选：C．‎ ‎9．如图所示，已知AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D，则∠DBC的度数（　　）‎ A．40° B．70° C．30° D．50°‎ 解：∵AB＝AC，∠A＝40°，‎ ‎∴∠ABC＝∠C＝70°，‎ ‎∵MN是AB的垂直平分线，‎ ‎∴DA＝DB，‎ ‎∴∠DBA＝∠A＝40°，‎ ‎∴∠DBC＝30°，‎ 故选：C．‎ ‎10．如果小球在如图所示的地面上自由滚动，并随机停留在某块方砖上，那么它最终停留在黑色区域的概率是（　　）‎ A． B． C． D．‎ 解：根据图示，‎ ‎∵黑色区域的面积等于6块方砖的面积，总面积等于16块方砖的面积，‎ ‎∴小球最终停留在黑色区域的概率是：‎ ‎＝．‎ 故选：D．‎ ‎11．一艘轮船和一艘快艇沿相同路线从甲港出发到乙港，行驶路程随时间变化的图象如图，下列结论错误的是（　　）‎ A．轮船的速度为20 km/h B．快艇的速度为 km/h ‎ C．轮船比快艇先出发2 h D．快艇比轮船早到2 h 解：由函数图象，得 A、轮船的速度为：160÷8＝20km/h，故A正确，‎ B、快艇的速度为：160÷（6﹣2）＝40km/h，故B错误，‎ C、由函数图象可以得出轮船比快艇先出发2h，故C正确，‎ D、快艇比轮船早到8﹣6＝2小时，故D正确；‎ 故选：B．‎ ‎12．如图，△ABD与△AEC都是等边三角形，AB≠AC，下列结论中，正确的个数是（　　），‎ ‎①BE＝CD；②∠BOD＝60°；③∠BDO＝∠CEO；④若∠BAC＝90°，且DA∥BC，则BC⊥CE．‎ A．1 B．2 C．3 D．4‎ 解：∵△ABD与△AEC都是等边三角形，‎ ‎∴AD＝AB，AE＝AC，∠ADB＝∠ABD＝60°，∠DAB＝∠EAC＝60°，‎ ‎∴∠DAB+∠BAC＝∠EAC+∠BAC，‎ ‎∴∠DAC＝∠BAE，‎ 在△DAC和△BAE中，，‎ ‎∴△DAC≌△BAE（SAS），‎ ‎∴BE＝DC，∠ADC＝∠ABE，‎ ‎∵∠BOD＝180°﹣∠ODB﹣∠DBA﹣∠ABE＝180°﹣∠ODB﹣60°﹣∠ADC＝120°﹣（∠ODB+∠ADC）＝120°﹣60°＝60°，‎ ‎∴∠BOD＝60°，∴①正确；②正确；‎ ‎∵△ABD与△AEC都是等边三角形，‎ ‎∴∠ADB＝∠AEC＝60°，但根据已知不能推出∠ADC＝∠AEB，‎ ‎∴∠BDO＝∠CEO错误，∴③错误；‎ ‎∵DA∥BC，‎ ‎∴∠DAB＝∠ABC＝60°，‎ ‎∵∠BAC＝90°，‎ ‎∴∠ACB＝30°，‎ ‎∵∠ACE＝60°，‎ ‎∴∠ECB＝90°，‎ ‎∴BC⊥CE，④正确，‎ 综上所述，①②④正确，‎ 故选：C．‎ 二、填空题（共6小题，每小题4分，满分24分）‎ ‎13．若（x+2）（x﹣4）＝x2+nx﹣8，则n＝　﹣2　．‎ 解：已知等式整理得：x2﹣2x﹣8＝x2+nx﹣8，‎ 则n＝﹣2，‎ 故答案为：﹣2‎ ‎14．在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球，任意摸出一球，摸到红球的概率是　　．‎ 解：∵袋子中共有8个球，其中红球有3个，‎ ‎∴任意摸出一球，摸到红球的概率是，‎ 故答案为：．‎ ‎15．已知（a+b）2＝16，ab＝6，则a2+b2的值是　244　．‎ 解：∵（a+b）2＝a2+2ab+b2＝256，ab＝6，‎ ‎∴a2+b2＝244，‎ 故答案为：244‎ ‎16．已知等腰三角形的两边长是3cm和6cm，则这个等腰三角形的周长是　15　cm．‎ 解：若3cm是腰长，则三角形的三边分别为3cm，3cm，6cm，‎ ‎∵3+3＝6，‎ ‎∴不能组成三角形，‎ 若3cm是底边，则三角形的三边分别为3cm，6cm，6cm，‎ 能组成三角形，‎ 周长＝3+6+6＝15cm，‎ 综上所述，这个等腰三角形的周长是15cm．‎ 故答案为：15．‎ ‎17．暑假里，小明爸爸开车带小明去青岛游玩，一路上匀速前行，小明记下了如下数据：‎ 观察时刻 ‎8：00‎ ‎8：06‎ ‎8：18‎ ‎（注：“青岛80km”表示离青岛的距离为80km）‎ 路牌内容 青岛80km 青岛70km 青岛50km 从8点开始，记汽车行驶的时间为t（min），汽车离青岛的距离为s（km），则s与t的关系式为　s＝80﹣t　．‎ 解：由表知，汽车每6min行驶10km，‎ ‎∴汽车的速度为＝（km/min），‎ 则s＝80﹣t，‎ 故答案为：s＝80﹣t．‎ ‎18．如图，△ABE和△ACD是△ABC分别以AB、AC为对称轴翻折180°形成的，若∠1：∠2：∠3＝29：4：3，则∠α的度数为　70°　．‎ 解：由题可得，∠ACB＝∠ACD，∠ABC＝∠EBA，‎ ‎∵∠1：∠2：∠3＝29：4：3，‎ ‎∴∠2+∠3＝180°×＝35°，‎ ‎∴∠α＝∠EBC+∠DCB＝2（∠2+∠3）＝2×35°＝70°，‎ 故答案为：70°．‎ 三、解答题（共9小题，满分78分，解答应写出必要的文字说明，证明过程或演算步骤）‎ ‎19．计算：‎ ‎（1）﹣12019﹣（）﹣2﹣（3.14﹣π）0‎ ‎（2）（ab3﹣2a2b2）÷ab+（a+b）•2a 解：（1）原式＝﹣1﹣4﹣1＝﹣6；‎ ‎（2）原式＝b2﹣2ab+2a2+2ab＝b2+2a2．‎ ‎20．先化简，再求值：（x﹣2y）2﹣（x+y）（x﹣y）﹣5y2，其中x＝，y＝﹣2‎ 解：原式＝x2﹣4xy+4y2﹣x2+y2﹣5y2‎ ‎＝﹣4xy，‎ 当x＝，y＝﹣2时，原式＝﹣4××（﹣2）＝4．‎ ‎21．如图，EF∥AD，∠BEF＝∠ADG，∠BAC＝80°，求∠AGD的度数．‎ 解：∵EF∥AD（已知）‎ ‎∴∠2＝∠3，‎ 又∵∠1＝∠2（已知），‎ ‎∴∠1＝∠3，‎ ‎∴AB∥DG，‎ ‎∴∠BAC+∠AGD＝180°，‎ ‎∵∠BAC＝80°（已知），‎ ‎∴∠AGD＝100°．‎ ‎22．如图，点B、F、C、E在同一条直线上，FB＝CE，AC∥DF，AC＝DF．求证：AB＝DE．‎ ‎【解答】证明：∵FB＝CE，‎ ‎∴BC＝EF，‎ ‎∵AC∥FD，‎ ‎∴∠ACB＝∠DFE（两直线平行，内错角相等），‎ 在△ABC和△DEF中，‎ ‎∴△ABC≌△DEF（SAS），‎ ‎∴AB＝DE．‎ ‎23．下面的方格图是由边长为1的42个小正方形拼成的，△ABC的顶点A、B、C均在小正方形的顶点上．‎ ‎（1）作出△ABC关于直线m对称的△A′B′C′；‎ ‎（2）求△ABC的面积．‎ 解：（1）如图，△A′B′C′为所作；‎ ‎（2）△ABC的面积＝3×3﹣×1×3﹣×2×1﹣×2×3＝3.5．‎ ‎24．元旦期间，某超市开展有奖促销活动，凡在超市购物的顾客均有转动圆盘的机会（如图），如果规定当圆盘停下来时指针指向8就中一等奖，指向2或6就中二等奖，指向1或3或5就中纪念奖，指向其余数字不中奖．‎ ‎（1）转动转盘中奖的概率是多少？‎ ‎（2）元旦期间有1000人参与这项活动，估计获得一等奖的人数是多少？‎ 解：（1）∵数字8，2，6，1，3，5的份数之和为6份，‎ ‎∴转动圆盘中奖的概率为：＝；‎ ‎（2）根据题意可得，获得一等奖的概率是，‎ 则元旦这天有1000人参与这项活动，估计获得一等奖的人数为：1000×＝125（人）．‎ ‎25．为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：‎ 汽车行驶时间t（h）‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ 油箱剩余油量Q（L）‎ ‎100‎ ‎94‎ ‎88‎ ‎82‎ ‎…‎ ‎（1）根据上表的数据，请你写出Q与t的关系式；‎ ‎（2）汽车行驶5h后，油箱中的剩余油量是多少？‎ ‎（3）该品牌汽车的油箱加50L，若以100km/h的速度匀速行驶，该车最多能行驶多远？‎ 解：（1）Q＝100﹣6t；‎ ‎（2）当t＝5时，Q＝100﹣6×5＝70．‎ 答：汽车行驶5h后，油箱中的剩余油量是70L；‎ ‎（3）当Q＝50时，50＝100﹣6t，‎ ‎ 6t＝50，‎ 解得：t＝，‎ ‎100×＝km．‎ 答：该车最多能行驶km．‎ ‎26．如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，点D是射线BC上一动点，过点B作BE⊥AD，垂足为点E，交直线AC于点P．‎ ‎（1）如图（1），若点D在BC的延长线上，且点E在线段AD上，试猜想AP，CD，BC之间的数最关系，并说明理由；‎ ‎（2）如图（2），若点D在线段BC上，试猜想AP，CD，BC之间的数量关系，并说明理由．‎ 解：（1）BC＝AP+CD，‎ 理由如下：∵∠ACB＝90°，BE⊥AD，‎ ‎∴∠D+∠DAC＝90°，∠D+∠DBE＝90°，‎ ‎∴∠DAC＝∠DBE，且∠ACB＝∠ACD，AC＝BC，‎ ‎∴△ACD≌△BCP（ASA），‎ ‎∴CD＝CP，‎ ‎∵BC＝AC＝CP+AP，‎ ‎∴BC＝AP+CD，‎ ‎（2）AP＝BC+CD，‎ 理由如下：∵∠ACB＝90°，BE⊥AD，‎ ‎∴∠P+∠PAE＝90°，∠P+∠PBC＝90°，‎ ‎∴∠PAE＝∠PBC，且∠ACB＝∠BCP，AC＝BC，‎ ‎∴△ACD≌△BCP（ASA），‎ ‎∴CD＝CP，‎ ‎∵AP＝AC+CP，‎ ‎∴AP＝BC+CD．‎ ‎27．如图，在长方形ABCD中，AB＝8cm，BC＝12cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒．‎ ‎（1）如图1，S△DCP＝　48﹣8t　．（用t的代数式表示）‎ ‎（2）如图1，当t＝3时，试说明：△ABP≌△DCP．‎ ‎（3）如图2，当点P从点B开始运动的同时，点Q从点C出发，以vcm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．‎ 解：（1）S△DCP＝•PC•CD＝•（12﹣2t）•8＝48﹣8t．‎ 故答案为48﹣8t．‎ ‎（2）当t＝3时，BP＝2×3＝6，‎ ‎∴PC＝12﹣6＝6，‎ ‎∴BP＝PC，‎ 在△ABP与△DCP中 ‎，‎ ‎∴△ABP≌△DCP（SAS）．‎ ‎（3）①当BP＝CQ，AB＝PC时，△ABP≌△PCQ，‎ ‎∵AB＝8，‎ ‎∴PC＝8，‎ ‎∴BP＝12﹣8＝4，‎ ‎∴2t＝4，解得：t＝2，‎ ‎∴CQ＝BP＝4，v×2＝4，解得：v＝2；‎ ‎②当BA＝CQ，PB＝PC时，△ABP≌△QCP，‎ ‎∵PB＝PC，‎ ‎∴BP＝PC＝6，‎ ‎∴2t＝6，解得：t＝3，‎ CQ＝AB＝8，v×3＝8，解得：，‎ 综上所述，当v＝2或时，△ABP与△PQC全等．‎