七年级下册数学第三章 变量之间的关系 周周测2（3-1~3-3） 北师大版

七年级下册数学第三章 变量之间的关系 周周测2（3-1~3-3） 北师大版

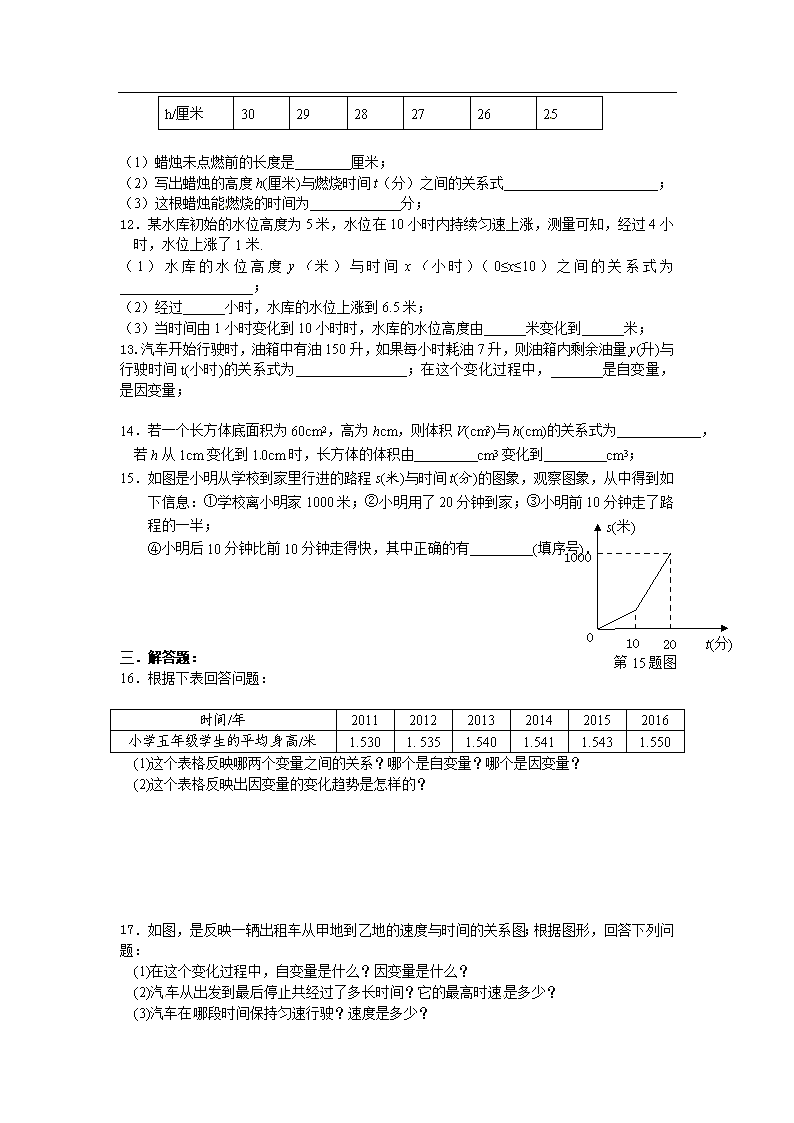
第三章 变量之间的关系 周周测2‎ 一．选择题：（四个选项中只有一个是正确的，选出正确选项填在题目相应括号内）‎ ‎1．某产品每件成本10元，试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表，下面能表示日销售量y(件)与销售价x(元)的关系式是 ( )‎ x(元)‎ ‎15‎ ‎20‎ ‎25‎ ‎…‎ y(件)‎ ‎25‎ ‎20‎ ‎15‎ ‎…‎ ‎ A．y＝x＋40 B．y＝－x＋15 C．y＝－x＋40 D．y＝x＋15‎ x/kg ‎0‎ ‎1[来源:Z§xx§k.Com]‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ y/cm ‎10‎ ‎10.5‎ ‎11‎ ‎11.5‎ ‎12‎ ‎12.5‎ ‎2． 弹簧挂上物体后会伸长，测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系：下列说法不正确的是 ( ) ‎ A．x与y都是变量，且x是自变量，y是因变量 B．弹簧不挂重物时的长度为0 cm C．物体质量每增加1 kg，弹簧长度y增加0.5 cm ‎ D．所挂物体质量为7 kg时，弹簧长度为13.5 cm ‎3．某大剧场地面的一部分为扇形，观众席的座位数按下列方式设置：‎ 排数(x)‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ 座位数(y)‎ ‎50‎ ‎53‎ ‎56‎ ‎59‎ ‎…‎ 下列结论：①排数x是自变量，座位数y是因变量；②排数x是因变量，座位数y是自变量；‎ ‎③y＝50＋3x；④y＝47＋3x，其中正确的结论有( )‎ A．1个 B．2个 C．3个 D．4个 ‎4．对于关系式y＝2x＋5，下列说法：①x是自变量，y是因变量；②x的数值可以任意选择；‎ ‎③y是变量，它的值与x无关；④这个关系式表示的变量之间的关系不能用图象表示；‎ ‎⑤y与x的关系还可以用表格和图象表示；其中正确的是 ( )‎ ‎ A．①②③ B．①②④ C．①③⑤ D．①②⑤‎ ‎5．升旗仪式上，国旗冉冉上升，下列哪个函数图象能近似地刻画上升的国旗离旗杆顶端的距离与时间的关系 ( )‎ ‎6．如图是我国古代计时器“漏壶”的示意图，在壶内盛一定量的水，水从壶底的小孔漏出；壶壁内画有刻度，人们根据壶中水面的位置计时，用x表示时间，y表示壶底到水面的高度，则y与x的变量关系式的图象是 ( )‎ ‎[来源:学科网]‎ ‎7．将一个球竖直向上抛起，球升到最高点，垂直下落，直到地面．在此过程中，球的高度与时间的关系可以用下图中的哪一幅来近似地刻画 ( )‎ ‎8．一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，两车离乙地的路程s(千米)与行驶时间t(小时)的关系如图所示，则下列结论中错误的是( )‎ A．相遇时快车行驶了150千米 B．慢车行驶速度为60千米/小时 C．甲、乙两地的路程是400千米 D．快车出发后4小时到达乙地 ‎9．如图，折线OEFPMN描述了某汽车在行驶过程中速度与时间的关系，下列说法中错误的是( )‎ ‎ A．第3分钟时汽车的速度是40千米/时 B．第12分钟时汽车的速度是0千米/时 ‎ C．从第9分钟到第12分钟，汽车的速度从60千米/时减少到0千米/时 ‎ D．从第3分钟到第6分钟，汽车停止[来源:Z#xx#k.Com]‎ S（千米）‎ ‎18‎ t（小时）‎ 甲 乙 O 第10题图 ‎0.5‎ ‎1‎ ‎2‎ ‎2.5‎ ‎ ‎ 第8题图 第9题图 ‎10．甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系的图象如图所示，根据图中提供的信息，有下列说法：‎ （1） 他们都行驶了18千米；（2）甲在途中停留了0.5小时；（3）乙比甲晚出发了0.5小时；‎ ‎（4）相遇后，甲的速度小于乙的速度；（5）甲、乙两人同时到达目的地。‎ 其中，符合图象描述的说法有（ ）‎ A．2个 B．4个 C．3个 D．5个 二．填空题：（把正确答案填在题目相应横线上）‎ ‎11.点燃一根蜡烛后，蜡烛的高度h(厘米)与燃烧时间t（分）之间的关系如下表：‎ t/分 ‎0‎ ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ h/厘米 ‎30‎ ‎29‎ ‎28‎ ‎27‎ ‎26‎ ‎25‎ ‎（1）蜡烛未点燃前的长度是________厘米；‎ ‎（2）写出蜡烛的高度h(厘米)与燃烧时间t（分）之间的关系式______________________；‎ ‎（3）这根蜡烛能燃烧的时间为_____________分；‎ ‎12．某水库初始的水位高度为5米，水位在10小时内持续匀速上涨，测量可知，经过4小时，水位上涨了1米.‎ ‎（1）水库的水位高度y（米）与时间x（小时）（0≤x≤10）之间的关系式为___________________；‎ ‎（2）经过______小时，水库的水位上涨到6.5米；‎ ‎（3）当时间由1小时变化到10小时时，水库的水位高度由______米变化到______米；‎ ‎13.汽车开始行驶时，油箱中有油150升，如果每小时耗油7升，则油箱内剩余油量y(升)与行驶时间t(小时)的关系式为 ；在这个变化过程中， 是自变量， 是因变量；‎ ‎14．若一个长方体底面积为60cm2，高为hcm，则体积V(cm3)与h(cm)的关系式为 ，‎ 若h从1cm变化到10cm时，长方体的体积由 cm3变化到 cm3；‎ ‎0‎ ‎10‎ ‎20‎ ‎1000‎ t(分)‎ s(米)‎ 第15题图 ‎15．如图是小明从学校到家里行进的路程s(米)与时间t(分)的图象，观察图象，从中得到如下信息：①学校离小明家1000米；②小明用了20分钟到家；③小明前10分钟走了路程的一半；‎ ‎④小明后10分钟比前10分钟走得快，其中正确的有 (填序号)． ‎ 三．解答题：‎ ‎16．根据下表回答问题：‎ 时间/年 ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ 小学五年级学生的平均身高/米 ‎1.530‎ ‎1. 535‎ ‎1.540‎ ‎1.541‎ ‎1.543‎ ‎1.550‎ ‎(1)这个表格反映哪两个变量之间的关系？哪个是自变量？哪个是因变量？‎ ‎(2)这个表格反映出因变量的变化趋势是怎样的？‎ ‎17．如图，是反映一辆出租车从甲地到乙地的速度与时间的关系图；根据图形，回答下列问题：‎ ‎(1)在这个变化过程中，自变量是什么？因变量是什么？‎ ‎(2)汽车从出发到最后停止共经过了多长时间？它的最高时速是多少？‎ ‎(3)汽车在哪段时间保持匀速行驶？速度是多少？[来源:Z§xx§k.Com]‎ ‎18．科学家研究发现，声音在空气中传播的速度y(米/秒)与气温x(℃)有关：当气温是0℃时，音速是331米/秒；当气温是5℃时，音速是334米/秒；当气温是10℃时，音速是337米/秒；当气温是15℃时，音速是340米/秒；当气温是20℃时，音速是343米/秒；当气温是25℃时，音速是346米/秒；当气温是30℃时，音速是349米/秒．‎ ‎(1)请用表格表示气温与音速之间的关系；‎ ‎(2)表格反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？‎ ‎(3)当气温是35℃时，估计音速y可能是多少？‎ ‎(4)用一个式子来表示两个变量之间的关系；‎ ‎19.如图①所示， 在△ABC中，AD是三角形的高，且AD＝6 cm，E是一个动点，由B向C移动，其速度与时间的变化关系如图②所示，已知BC＝9 cm；‎ ‎(1)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式；‎ A B C ‎ D E ‎0‎ ‎2‎ ‎3‎ A 速度（cm/s）‎ 时间（s）‎ 图 ①‎ 图 ②‎ ‎(2)当E点停止后，求△ABE的面积；‎ ‎20．汽车在山区行驶过程中，要经过上坡、下坡、平路等路段，在自身动力不变的情况下，上坡时速度越来越慢，下坡时速度越来越快乐，平路上保持匀速行驶，如图表示了一辆汽车在山区行驶过程中，速度随时间变化的情况．‎ ‎(1)汽车在哪些时间段保持匀速行驶？时速分别是多少？‎ ‎(2)汽车遇到了几个上坡路段？几个下坡路段？在哪个下坡路段上所花时间最长？‎ ‎(3)大致描述这辆汽车的行驶情况，包括遇到的山路，在山路上的速度变化情况等．‎ ‎ ‎ 第三章 变量之间的关系 周周测2参考答案与解析 ‎1~10 CBBDA CCADB ‎11．(1)30；(2)h=30-0.5t；(3)60；‎ ‎12．（1）y=0.25x+5；（2）6；（3）5.25，7.5；[来源:学科网ZXXK]‎ ‎13．y＝－7t＋55；时间t；剩余油量y；‎ ‎14. V＝60h；60； 600； ‎ ‎15． ①②④；‎ ‎16．(1) 表格反映的是小学五年级学生的平均身高与时间之间的关系；‎ 时间是自变量，小学五年级学生的平均身高是因变量；‎ ‎(2)小学五年级学生的平均身高随时间的增加而增高；‎ ‎17．(1) 自变量是时间，因变量是速度．‎ ‎(2) 根据速度与时间图象的横坐标可知：‎ 汽车从出发到最后停止共经过了60分钟时间，最高时速是85千米/时．‎ ‎(3) 汽车在出发后35分钟到50分钟之间保持匀速，速度是85千米/时．‎ ‎(4) 汽车先加速行驶至第10分钟，然后减速行驶至第25分钟，接着停下5分钟，再加速行驶至第35分钟，然后匀速行驶至第50分钟，再减速行驶直至第60分钟停止．‎ ‎18．(1)‎ x(℃)‎ ‎0‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ ‎…‎ y(米/秒)‎ ‎331‎ ‎334‎ ‎337‎ ‎340‎ ‎343‎ ‎346‎ ‎…‎ ‎(2)音速和温度，温度是自变量，音速是因变量； ‎ ‎(3)352米/秒；‎ ‎(4)y＝331＋x.‎ ‎19．（1）y＝9x；（2）27cm2；‎ ‎20．(1)汽车在0.2～0.4h，0.6～0.7h，0.9～1h三个时间段保持匀速行驶，‎ 速度分别是70km/h，80km/h和70km/h； ‎ ‎(2)汽车遇到CD、FG两个上坡路段，AB、DE、GH三个下坡路段，在AB下坡路段上所花时间最长； ‎ ‎(3)汽车下坡行驶0.2h后转入平路行驶至0.4h，转入上坡行驶至0.5h，接着转入下坡行驶至0.6h，‎ 转入平路行驶至0.7h后又上坡行驶至0.8h，紧接着转入下坡行驶至0.9h，‎ 最后平路行驶至1h结束．‎