探索三角形全等的条件教案(2)(1)

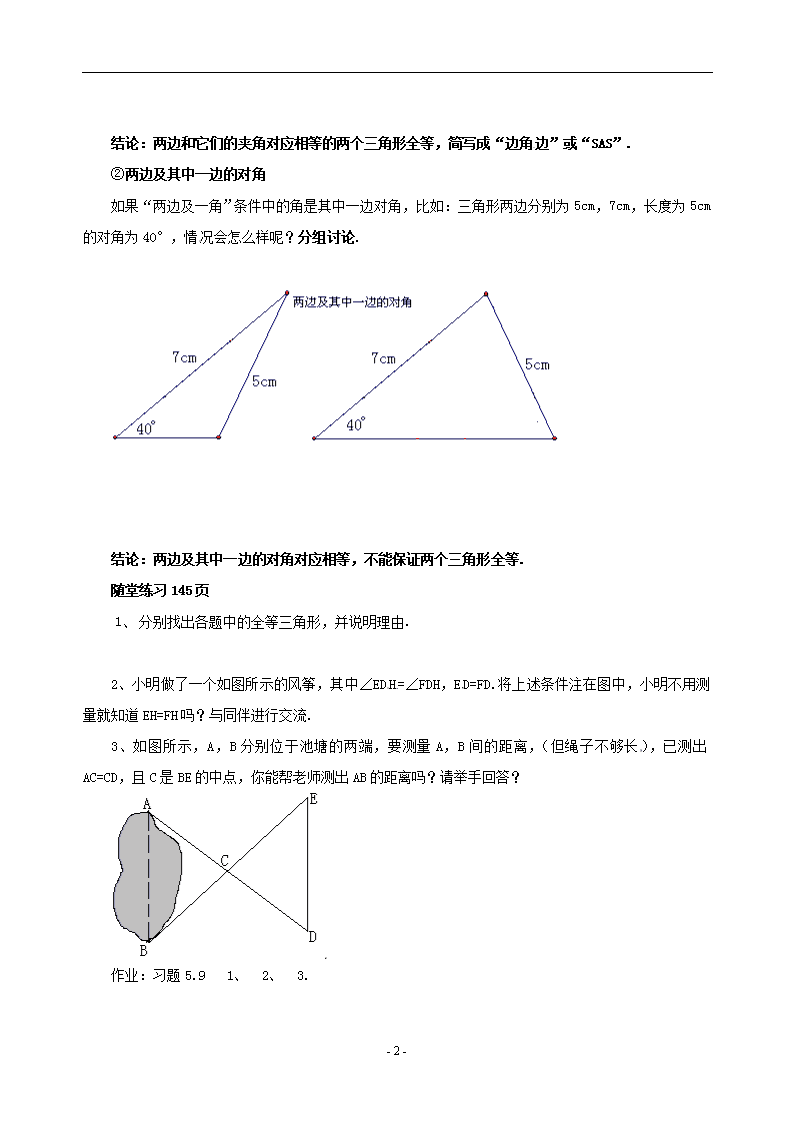
探索三角形全等的条件教案(2)(1)

‎ ‎ 探索三角形全等的条件（三）‎ ‎[教学目标]‎ 经历用两边一角画三角形，把所画的三角形进行重叠验证，探索全等三角形的条件之一“SAS”，并能应用它来判定两个三角形全等.‎ ‎[重点]掌握全等三角形的条件“SAS”及应用. ‎ ‎[难点]两边及其中一边的对角对应相等的两个三角形不全等的理解.‎ ‎[教学准备] 作图工具，剪刀，挂历纸或其它纸.‎ ‎[教学过程]‎ 1、 复习提问：‎ ‎①判断三角形全等至少需要几个条件？‎ ‎②你能用几种方法来判定两个三角形全等？‎ ‎2、导入新课：如果已知一个三角形的两边及一角，那么有几种情况呢？每种情况下得到的三角形都全等吗？[两边及夹角]、[两边及其中一边的对角]‎ 做一做 ① 两边及夹角 如果“两边及一角”条件中的角是两边的夹角，比如三角形两边分别为5cm，7cm，它们所夹的角为40°，你画的三角形与同伴画的一定全等吗？分组讨论.‎ 改变上述条件中的角度和边长，如：边长3cm，角45°和边长4cm，再试一试.‎ - 2 -‎ ‎ ‎ 结论：两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”.‎ ‎②两边及其中一边的对角 如果“两边及一角”条件中的角是其中一边对角，比如：三角形两边分别为5cm，7cm，长度为5cm的对角为40°，情况会怎么样呢？分组讨论.‎ 结论：两边及其中一边的对角对应相等，不能保证两个三角形全等.‎ 随堂练习145页 1、 分别找出各题中的全等三角形，并说明理由.‎ ‎2、小明做了一个如图所示的风筝，其中∠EDH=∠FDH，ED=FD.将上述条件注在图中，小明不用测量就知道EH=FH吗？与同伴进行交流.‎ ‎3、如图所示，A，B分别位于池塘的两端，要测量A，B间的距离，（但绳子不够长），已测出AC=CD，且C是BE的中点，你能帮老师测出AB的距离吗？请举手回答？‎ 作业：习题5.9 1、 2、 3. ‎ - 2 -‎