七年级下数学课件《平行线的判定和性质的应用》课件_冀教版

七年级下数学课件《平行线的判定和性质的应用》课件_冀教版

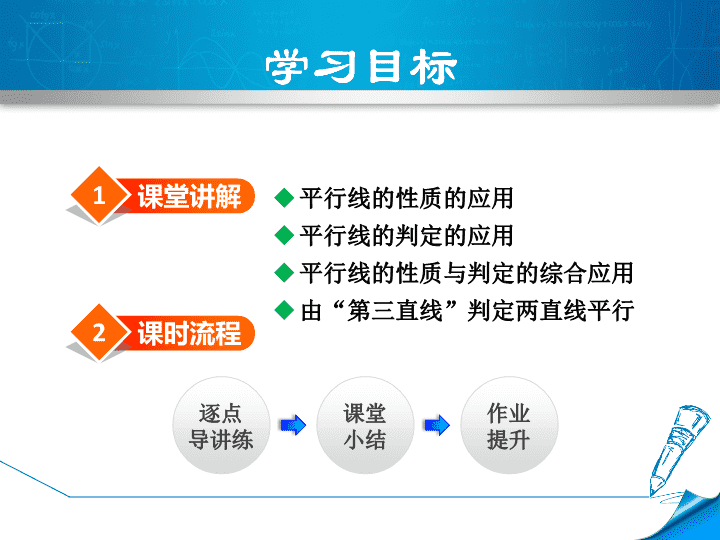
第七章相交线与平行线7.5平行线的性质第3课时平行线的判定和性质的应用 1课堂讲解平行线的性质的应用平行线的判定的应用平行线的性质与判定的综合应用由“第三直线”判定两直线平行2课时流程逐点导讲练课堂小结作业提升 复习回顾平行线的三个性质：两直线平行，同位角相等．两直线平行，内错角相等．两直线平行，同旁内角互补． 1知识点平行线的性质的应用下图是一块梯形铁片的残余部分，量得∠A=100°，∠B=115°，梯形的另外两个角分别是多少度？知1－讲例1 知1－讲因为梯形上、下两底AB与DC互相平行，根据“两直线平行，同旁内角互补”，可得∠A与∠D互补，∠B与∠C互补.于是∠D=180°-∠A=180°-100°=80°，∠C=180°-∠B=180°-115°=65°.所以梯形的另外两个角分别是80°，65°.解： 知1－讲如图，已知DA⊥AB，DE平分∠ADC，CE平分∠BCD，且∠1＋∠2＝90°，试说明BC⊥AB.例2 要说明BC⊥AB，即说明∠B＝90°.因为DA⊥AB，所以若能说明AD∥CB，则BC⊥AB.由DE平分∠ADC，CE平分∠BCD，且∠1＋∠2＝90°，可说明∠ADC＋∠BCD＝180°，从而说明AD∥BC.知1－讲导引： 因为DE平分∠ADC，CE平分∠BCD，所以∠1＝∠3，∠2＝∠4(角平分线的定义)．因为∠1＋∠2＝90°，所以∠1＋∠2＋∠3＋∠4＝180°，即∠ADC＋∠BCD＝180°.所以AD∥BC(同旁内角互补，两直线平行)，所以∠A＋∠B＝180°(两直线平行，同旁内角互补)．知1－讲解： 因为DA⊥AB，所以∠A＝90°(垂直定义)．所以∠B＝90°，所以BC⊥AB(垂直定义)．知1－讲 总结知1－讲平行线和角的大小关系、直线的位置关系等是紧密联系在一起的，通过同位角相等或内错角相等或同旁内角互补可以判断两直线平行，反过来可以根据两直线平行判断同位角相等、内错角相等或同旁内角互补，再利用这些相等、互补关系说明其他结论；因此两直线平行好似一座桥梁，将原本没有关系的数学问题建立起联系． 1【中考·遵义】如图，在平行线a，b之间放置一块直角三角尺，三角尺的顶点A，B分别在直线a，b上，则∠1＋∠2的值为()A．90°B．85°C．80°D．60°知1－练A 2【中考·邵阳】如图所示，要在一条公路的两侧铺设平行管道，已知一侧铺设的角度为120°，为使管道对接，另一侧铺设的角度大小应为()A．120°B．100°C．80°D．60°知1－练D 3【中考·湖州】如图是我们常用的折叠式小刀，刀柄外形是一个长方形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图所示的∠1与∠2，则∠1与∠2的度数和是__________度．知1－练90 2知识点平行线的判定的应用知2－讲例3如图所示，∠B＝∠D，∠CEF＝∠A.试问CD与EF平行吗？为什么？ 知2－讲导引：1.要说明CD∥EF，我们无法找出相等的同位角、内错角，也无法说明其同旁内角互补，因此需找第三条直线与它们平行(即AB∥CD，AB∥EF)，这都能由已知∠B＝∠D，∠CEF＝∠A说明．2.由已知∠B＝∠D，∠CEF＝∠A很容易就能得出AB∥CD及EF∥AB，再由如果两条直线都和第三条直线平行，那么这两条直线也互相平行就可得到CD∥EF. 知2－讲解：CD∥EF，理由：∵∠B＝∠D，∴AB∥CD(内错角相等，两直线平行)．∵∠CEF＝∠A，∴EF∥AB(同位角相等，两直线平行)．∴CD∥EF(平行于同一条直线的两条直线平行)． 总结知2－讲找寻说明平行的方法：1.分析法：由结论往前推，要说明这个结论成立需要什么样的条件，一直递推到已知条件为止；(如导引1)2.综合法：由已知条件一步一步往后推理，看这个已知条件能推出什么结论,一直推导出要说明的结论为止;(如导引2)3.两头凑：当遇到复杂问题的时候，我们常常将分析法和综合法同时进行，即由两头向中间推，寻找到中间的结合点． 知2－讲例4光线从空气射入水中时，传播方向会发生改变，这种现象叫做光的折射现象．同样，光线从水中射入空气中时，也会发生折射现象，一束光线从空气射入水中再从水中射入空气中时，光线的传播方向如图，其中，直线a，b都表示空气与水的分界面．已知∠1＝∠4，∠2＝∠3，请你判断光线c与d是否平行？为什么？ 知2－讲导引：设光线在水中的部分为e，e与直线a所成的钝角为∠5，e与直线b所成的钝角为∠6，只要能说明∠1＋∠5＝∠4＋∠6，则根据“内错角相等，两直线平行”即可判定c∥d. 知2－讲解：c∥d.理由如下：如图，设光线在水中的部分为e.∵∠2＋∠5＝180°，∠3＋∠6＝180°，∠2＝∠3，∴∠5＝∠6(等角的补角相等)．又∵∠1＝∠4，∴∠1＋∠5＝∠4＋∠6.∴c∥d(内错角相等，两直线平行)． 总结知2－讲判断光线c与d是否平行，应首先解决两个关键问题，一是把实物图抽象为“三线八角”的基本图形；二是把直线c，d看作被直线e所截的两条直线．如此，问题转化为说明∠1＋∠5＝∠4＋∠6. 1如图，已知BE平分∠ABC，CF平分∠BCD，∠1＝∠2，那么直线AB与CD的位置关系是________．知2－练平行 2【中考·枣庄】如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（　　）A．15°B．22.5°C．30°D．45°知2－练A 3知识点平行线的性质与判定的综合应用知3－讲平行线的性质与判定之间既有联系又有区别，一定不可混淆二者的条件和结论，要把它们严格区别开来．分类条件结论平行线的判定同位角相等两直线平行内错角相等同旁内角互补平行线的性质两直线平行同位角相等内错角相等同旁内角互补 知3－讲例5如图，已知∠ABC与∠ECB互补，∠1＝∠2，则∠P与∠Q一定相等吗？说说你的理由．导引：如果∠P和∠Q相等，那么PB∥CQ，∴要判断∠P与∠Q是否相等，只需判断PB和CQ是否平行．要说明PB∥CQ，可以通过说明∠PBC＝∠BCQ来实现，由于∠1＝∠2，因此只需说明∠ABC＝∠BCD即可． 知3－讲解：∠P＝∠Q.理由如下：∵∠ABC与∠ECB互补(已知)，∴AB∥ED(同旁内角互补，两直线平行)．∴∠ABC＝∠BCD(两直线平行，内错角相等)．∵∠1＝∠2(已知)，∴∠ABC－∠1＝∠BCD－∠2(等式的性质)，即∠PBC＝∠BCQ.∴PB∥CQ(内错角相等，两直线平行)．∴∠P＝∠Q(两直线平行，内错角相等)． 总结知3－讲一个数学问题的构成含有四个要素：题目的条件、解题的依据、解题的方法、题目的结论，如果题目所含的四个要素解题者已经知道或者结论虽未指明，但它是完全确定的，这样的问题就是封闭性的数学问题． 1【中考·宿迁】如图，直线a，b被直线c，d所截，若∠1＝80°，∠2＝100°，∠3＝85°，则∠4的度数是（　　）A．80°B．85°C．95°D．100°知3－练B 2【中考·潍坊】如图，∠BCD＝90°，AB∥DE，则∠α与∠β满足（　　）A．∠α＋∠β＝180°B．∠β－∠α＝90°C．∠β＝3∠αD．∠α＋∠β＝90°知3－练B 4知识点由“第三直线”判定两直线平行知4－讲如图,你能说出木工用图中的角尺画平行线的道理吗? 总结知4－讲平行于同一条直线的两直线平行. 知4－讲如图，已知∠1＝∠A，∠2＝∠B，那么MN与EF平行吗？如果平行，请说明理由．例6 知4－讲解：MN与EF平行．理由如下：∵∠1＝∠A，∴MN∥AB(内错角相等，两直线平行)，∵∠2＝∠B，∴EF∥AB(同位角相等，两直线平行)，∴MN∥EF(平行于同一条直线的两条直线平行)． 总结知4－讲在同一平面内和一条直线平行的直线也互相平行． 知4－练在同一个平面内，不重合的两个直角，如果它们有一条边共线，那么另一条边()A．互相平行B．互相垂直C．共线D．互相平行或共线1D 知4－练三条直线a，b，c，若a∥c，b∥c，则a与b的位置关系是()A．a⊥bB．a∥bC．a⊥b或a∥bD．无法确定2B 知2－练如图，已知AB⊥BD于点B，CD⊥BD于点D，∠1＝∠2，试问CD与EF平行吗？为什么？解：CD∥EF.理由：因为∠1＝∠2(______)，所以AB∥EF(_________________________)．因为AB⊥BD，CD⊥BD，所以AB∥CD(____________________________________________)．所以CD∥EF(______________________________)．3已知同位角相等，两直线平行在同一平面内，垂平行于同一条直线的两条直线平行直于同一条直线的两条直线平行 两直线平行同位角相等内错角相等同旁内角互补平行线的判定平行线的性质线的关系角的关系性质角的关系线的关系判定平行线的判定与平行线的性质的关系：1知识小结 如图，已知∠ABC，请你再画一个∠DEF，使DE∥AB，EF∥BC，且DE交BC边于点P.探究：∠ABC与∠DEF有怎样的数量关系？并说明理由．2易错小结易错点：画图考虑不周导致漏解. 解：画图如图①②③④所示．∠ABC与∠DEF相等或互补，理由如下：如图①，∵AB∥DE，∴∠ABC＝∠DPC.∵BC∥EF，∴∠DEF＝∠DPC.∴∠ABC＝∠DEF.如图②，∵AB∥DE，∴∠ABC＝∠EPC.∵BC∥EF，∴∠EPC＝∠DEF.∴∠ABC＝∠DEF.如图③，∵AB∥DE，∴∠ABC＝∠BPE.∵BC∥EF，∴∠DEF＋∠BPE＝180°.∴∠ABC＋∠DEF＝180°. 本题易错之处在于学生往往只考虑到其中两种情况，而漏掉另外两种情况．如图④，∵AB∥DE，∴∠ABC＝∠EPC.∵BC∥EF，∴∠EPC＋∠DEF＝180°.∴∠ABC＋∠DEF＝180°.综上可知，∠ABC与∠DEF相等或互补． 请完成《典中点》Ⅱ、Ⅲ板块对应习题！