七年级下册数学课件《同底数幂的除法》 (3)_北师大版

七年级下册数学课件《同底数幂的除法》 (3)_北师大版

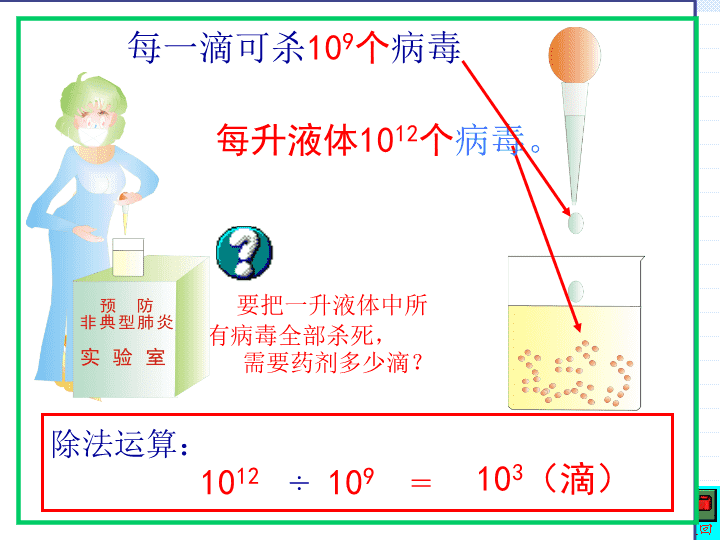
第三节同底数幂的除法（义务教育课程标准实验教科书） 2003年几乎蔓延全国的流行性“非典型肺炎”（简称“非典”），经专家的研究，发现是由一种“病毒”引起的，现有一瓶含有该病毒的液体，其中每升含有1012个病毒。医学专家进行了实验，发现一种药物对它有特殊的杀灭作用，每一滴这种药物，可以杀死109个病毒。现在要把一升液体中的所有病毒全部杀死，需要这种药剂多少滴？ 要把一升液体中所有病毒全部杀死，需要药剂多少滴？除法运算：1012÷109=103（滴）每升液体1012个病毒。每一滴可杀109个病毒 做一做计算下列各式，并说明理由（m>n）(1)108÷105=(2)10m÷10n=(3)(-3)m÷(-3)n= 解题思路解：（根据幂的定义)(1)108÷105=10●10●10●10●10●10●10●10有8个1010●10●10●10●10有5个10=108-5=103 解题思路解：（根据幂的定义)(2)10m÷10n=10●10………10有m个1010●10………10有n个10=10m-n 解题思路解：（根据幂的定义)(3)(-3)m÷(-3)n=(-3)●(-3)……(-3)有m个(-3)(-3)●(-3)……(-3)n个(-3)=(-3)m-n ——同底数幂的除法的一般规律am÷an=a●a●a………a有m个aa●a●a………a有n个a总结规律=am-nam÷an=(a≠0,m,n都是正整数，且m>n)am-n同底数幂相除，底数，指数。不变相减 例题解析例题解析【例1】计算：(1)a7÷a4;(2)(-x)6÷(-x)3;(3)(xy)4÷(xy);(4)b2m+2÷b2.=a7–4=a3;(1)a7÷a4解：(2)(-x)6÷(-x)3=(-x)6–3=(-x)3(3)(xy)4÷(xy)=(xy)4–1(4)b2m+2÷b2=b2m+2–2=-x3;=(xy)3=x3y3=b2m.注意最后结果中幂的形式应是最简的.①幂的指数、底数都应是最简的；②幂的底数是积的形式时，要再用一次(ab)n=anbn.②底数中系数不能为负； 2、讨论下列问题：(1)同底数幂相除法则中各这字母必须满足什么条件？a÷a=(a≠0,m,n都是正整数,且m＞n)mnam-n同底数幂相除，底数_____,指数______.不变相减(2)要使也能成立，你认为应当规定等于多少？呢？(3)要使和也成立，应当规定和分别等于多少呢？ 零指数幂、负指数幂的理解∴规定a0=1；am–mam÷am==a0，1=当p是正整数时，=a0÷ap=a0–p=a–p∴规定： 正整数指数幂的扩充想一想321猜一猜？0–1–2–33210–1–2–3我们规定：a0—零指数幂；a–p—负指数幂。 规定:a=1,(a≠0)0a=(a≠0,p是正整数)任何不等于零的数的零次幂都等于1。任何不等于零的数的-P(P是正整数)次幂，等于这个数的P次幂的倒数。 我们规定：1.我们知道了指数有正整数，还有负整数、零。a0=1，（a≠0），a-p=（a≠0，且p为正整数） 过手训练：判断正误，并改正，，得2=3 2.用小数或整数表示下列各负整数指数幂的值： 拓展练习找规律个0n个0n(n为正整数) 例2：用小数或分数表示下列各数：（1）10-3==（2）80╳8-2==（3）1.6╳10-4===0.0011╳1.6╳1.6╳0.0001=0.00016注意a0=1、 习题计算：（1）213÷27=（2）a11÷a5=（3）(-x)7÷(-x)=（4）(-ab)5÷(-ab)2=（5）62m+1÷6m=213-7=26=64a11-5=a6(-x)7-1=(-x)6=x6(-ab)5-2=(-ab)3=-a3b362m+1-m=6m+1 习题下面的计算是否正确？如有错误，请改正：（1）a6÷a1=a（2）b6÷b3=b2（3）a10÷a9=a（4）(-bc)4÷(-bc)2=-b2c2错误，应等于a6-1=a5错误，应等于b6-3=b3正确。错误，应等于(-bc)4-2=(-bc)2=b2c2 课外扩展计算：（1）(a-b)7÷(b-a)3=（2）m19÷m14╳m3÷m=（3）(b2)3╳(-b3)4÷(b5)3=（4）98╳272÷(-3)18=-(a-b)4m7b381 思考●探索●交流若aX=3,ay=5,求:（1）aX-y的值？（2）a3x-2y的值？352725 本节课你的收获是什么？小结本节课你学到了什么?同底幂的除法运算法则:am÷an=am–na0=1规定：个0个0(n为正整数);nn 同学们再见