七年级上册数学课件《应用一元一次方程—水箱变高》 (2)_北师大版

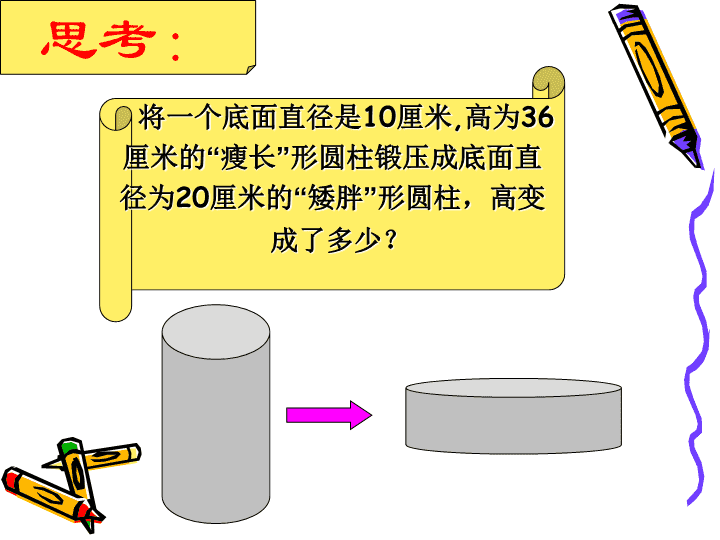
七年级上册数学课件《应用一元一次方程—水箱变高》 (2)_北师大版

从前有一个叫狙公的人养了一群猴子。每一天他都给足够的栗子给猴子吃，猴子高兴他也快乐。有一天他发现如果再这样喂猴子的话，，等不到下一个栗子的收获季节，他和猴子都会饿死，于是他想了一个办法，并且把这个办法说给猴子听，当猴子听到只能早上吃四个，晚上吃三个栗子的时候很是生气，呲牙咧嘴的。没办法狙公只好说早上三个，晚上四个，没想到猴子一听高兴的直打筋斗。朝三暮四：3+4＝4+3 4.我变胖了 思考：将一个底面直径是10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径为20厘米的“矮胖”形圆柱，高变成了多少？ 1、哪些量改变了？2、哪些量没变？（底面半径、高）（体积、重量）锻压3、你发现有什么相等关系？4、你能用你的语言表达出来吗？5、你能用数学表达式表示出来吗？ 分析高底面半径体积锻压前锻压后1036π×52×36π×102x5x根据等量关系，列出方程：π×52×36=π×102x解得：x=9因此，高变成了厘米。9 想一想：1.把一根铁丝围成一个长方形，有多少种围法？2.它们的周长改变了吗？3.它们的面积都相等吗？ 练一练：用一根长为10米的铁丝围成一个长方形。（1）使得该长方形的长比宽多1.4米，此时长方形的长、宽各为多少米？（2）使得该长方形的长比宽多0.8米，此时长方形的长、宽各为多少米？它所围成的长方形与（1）中所围长方形相比，面积有什么变化？（3）使得该长方形的长与宽相等，即围成一个正方形，此时正方形的边长是多少米？它所围成的面积与（1）（2）比较，哪个的面积大？ 解：(1)设此时长方形的宽为x米，x+x+1.4=10÷22x=3.6x=1.8长方形的长为1.8+1.4=3.2此时长方形的长为3.2米，宽为1.8米。则它的长为（x+1.4）米，根据题意，得xx+1.4 （2）设此时长方形的宽为x米，x+x+0.8=10÷22x=4.2x=2.1长方形的长2.1+0.8＝2.9则它的长为（x+0.8）米，根据题意，得∴长方形的长为2.9米，宽为2.1米，S=2.9×2.1＝6.09米2，()（1）中的长方形围成的面积：3.2×1.8＝5.76米2()比（1）中面积增大6..09－5.76＝0.33米2()x+0.8x X(3)设此时正方形的边长为x米，x+x=10÷2x=2.5正方形的边长为2.5米，根据题意，得比（2）中面积增大6.25－6.09＝0.16(米2)S=2.5×2.5＝6.25(米2)同样长的铁丝可以围更大的地方围成正方形时面积最大 1.墙上钉着用一根彩绳围成的梯形形状的饰物，如图实线所示。小颖将梯形下底的钉子去掉，并将这条彩绳钉成一个长方形，如图虚线所示。小颖所钉长方形的长、宽各为多少厘米？随堂练习：6610101010 小明要考考你了!小明的爸爸想用35米竹篱笆在墙边围成一个鸡棚（墙长14米），使长比宽大5米；小明的妈妈说这样不行，还是使长比宽大2米吧，你知道小明的妈妈是怎么想的吗？竹篱笆墙面xX+5 若小明用35米竹篱笆在墙边围成一个长方形鸡棚，使长比宽大2米，但在宽的一边有一扇1米宽的门，那么，请问小明围成的鸡棚的长和宽是多少呢？门墙面竹篱笆思考： 本节课收获1、锻压前体积=锻压后体积锻压前重量=锻压后重量2、长方形周长不变时，长方形的面积随着长与宽的变化而变化，当长与宽相等时，面积最大。 再见